10.Закон ома для цепи переменного тока

Рассмотрим цепь с последовательно соединенными активным сопротивлением - R , индуктивностью – L и емкостью – С.

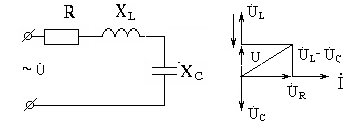
Для векторов действующих напряжений , и запишем второй закон Кирхгофа:

Складывая эти вектора графически и, учитывая, что вектор напряжения на активном сопротивлении - совпадает по фазе с вектором тока, вектор напряжения на индуктивности - опережает ток на угол π/2, а вектор напряжения на емкости - отстает от вектора тока на угол π/2, получим прямоугольный треугольник напряжений, гипотенуза которого равна полному напряжению - , а катеты равны активному напряжению - и реактивному напряжению - ( ) :

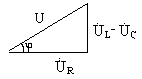
Из треугольника напряжений видно, что:

Если разделить все стороны прямоугольного треугольника напряжений на общий ток , то получим подобный ему треугольник сопротивлений, гипотенуза которого равна полному сопротивлению цепи - , а катеты - активному и реактивному сопротивлению цепи - и ( ) :

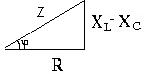
Из этого треугольника можно найти полное сопротивление цепи и записать закон Ома для цепи переменного синусоидального тока:

11.Резонанс напряжений,условия его возникновения и практическое значение

Резонанс напряжений возможен на участке цепи с последовательным соединением индуктивного и емкостного элемента.

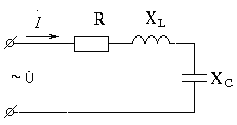
Угол сдвига фаз при резонансе равен нулю. Такой угол сдвига фаз можно получить тремя способами: изменением частоты напряжения питания, изменением индуктивности или емкости . Из треугольника сопротивлений следует, что: , следовательно при . Выражение называют условием резонанса напряжений. Из этого выражения следует, что и , где - резонансная частота. Полное сопротивление при резонансе равно активному сопротивлению и минимально при заданном . Ток максимален. Напряжения на участках контура с реактивными элементами равны ( ). Напряжение на участке с активным элементом равно напряжению питания на выводах контура и совпадает с ним по фазе: .

Если , то , т.е. напряжение на участках с реактивными элементами больше, чем напряжение питания. Это свойство – усиление напряжения – является важнейшей особенностью резонанса напряжений и широко используется в технике. Коэффициент усиления напряжения равен добротности контура - Q:

Величина называется характеристическим или волновым сопротивлением цепи. Активная мощность при резонансе максимальна ( , а ток максимален ) и равна полной мощности . Реактивная мощность равна нулю: .

Из векторной диаграммы видно, что при резонансе, несмотря на наличие в цепи индуктивности и емкости, ток совпадает по фазе с напряжением, т.е. индуктивное и емкостное напряжения компенсируют друг друга.

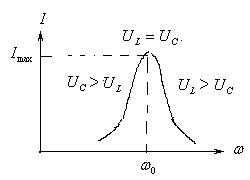
График зависимости силы тока от частоты называют амплитудно-частотной характеристикой. На резонансной частоте величина тока максимальна. На графике амплитудно-частотной характеристики различают три области: до резонанса ( ), резонанса ( ) и после резонанса ( ).

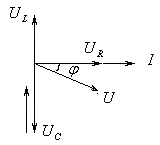
В до резонансе электрическая цепь имеет емкостной характер т.к.

(рис.а)

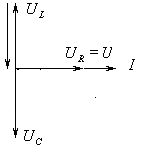
а) в) с)

В резонансе электрическая цепь имеет активный характер, т.к. (рис .в).

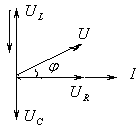
В после резонансе электрическая цепь имеет индуктивный характер, т.к. (рис. с)

Резонанс напряжений в промышленных электрических установках - нежелательное и опасное явление, т.к. может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике и электронике в приборах и устройствах, основанных на резонансном явлении.