Обчислення інтегралів

Пакет дозволяє символьно та чисельно обчислювати як звичайні, так і криволінійні інтеграли, крім того, серед них – багато інтегралів, підінтегральні функції яких мають особливості на кінцях відрізка інтегрування. Для вводу знаку операції інтегрування потрібно натиснути клавішу “&”, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку Визначений інтеграл. В результаті на екрані з’явиться знак операції з чотирма покажчиками:

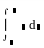
Для означення і обчислення інтеграла необхідно замість активного покажчика задати підінтегральну функцію, після знака диференціала (d) потрібно означити змінну інтегрування, а замість покажчиків, що є знизу і зверху знаку інтеграла, вказати дійсні вирази, які визначають відповідно значення нижньої і верхньої меж інтегрування.

В якості меж інтегрування повинні бути тільки дійсні вирази, тоді як підінтегральна функція може бути як дійсною, так і комплексною. Крім змінної інтегрування (ім’я якої повинне задовольняти умови пакету), інші змінні і константи, які використовуються в конструкції, повинні бути попередньо означені.

Подібно до випадку обчислення похідних пакет в якості меж інтегрування, а також констант і змінних підінтегрального виразу, допускає використання ранжованих змінних, що дає можливість виводити результати обчислення інтеграла у вигляді вихідних таблиць. Дана можливість дозволяє отримувати досить точні графіки первісних функцій.

Поряд з однократними пакет дозволяє обчислювати також m-кратні інтеграли, для чого в конструкцію вводяться підряд знаки інтеграла за числом (m) кратності інтеграла, що обчислюється. Але до m-кратних інтегралів потрібно звертатися тільки у випадку крайньої необхідності, тому що з ростом кратності різко зростає час їх обчислення.

Комплексні числа

Комплексне число задається в алгебраїчній формі як , де – дійсна частина комплексного числа , і – уявна частина . Якщо , комплексне число виводиться як дійсне, а якщо , – як уявне. Значення задається в полосі зі щотчиком Поріг для комплексних чисел (Сomplex Threshold) на закладці Допуск (Tolerance).

Комплексне спряження виводиться символом подвійних лапок після набрання імені змінної ( ).

Для роботи з комплексними числами пакет має такі функції:

1. Re(z) – дійсна частина числа;

2. Im(z) – уявна частина числа;

3. arg(z) – аргумент (кут в комплексній площині між додатнім напрямом осі ох і z);

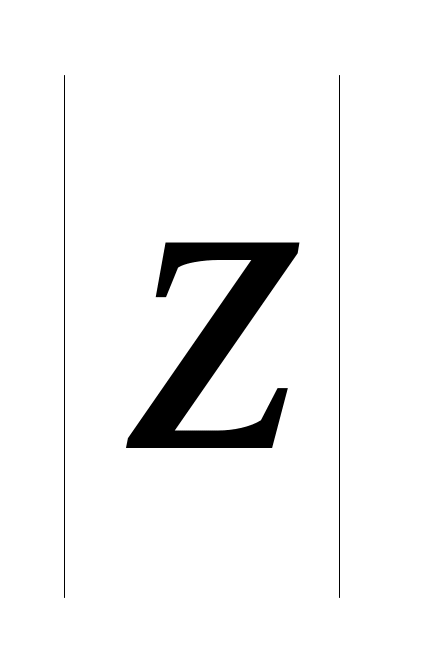4. – модуль ;

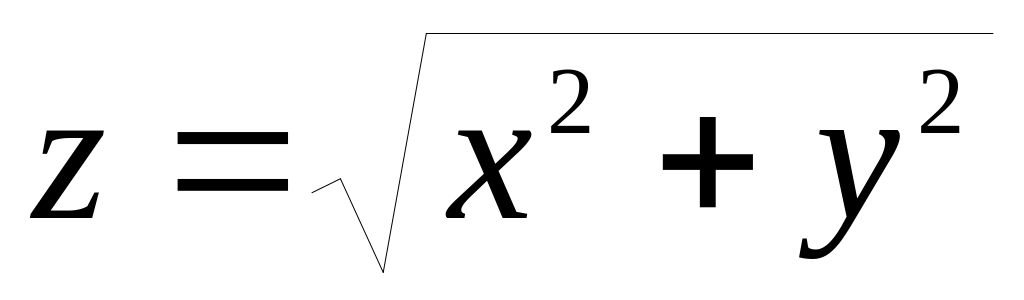5. csgn(z) – повертає або 0, якщо 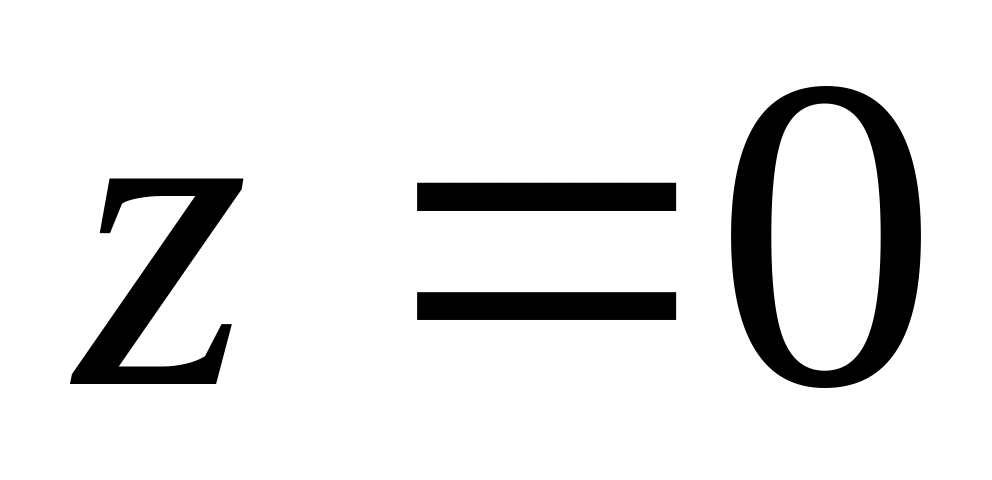, або 1, якщо , або якщо і 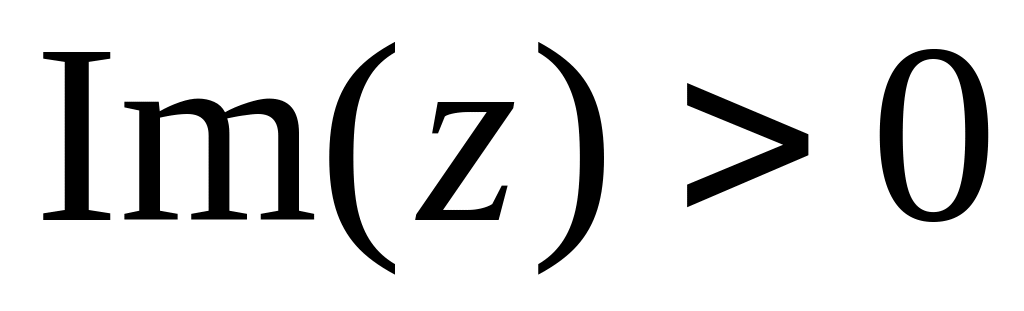, або – 1 в інших випадках;

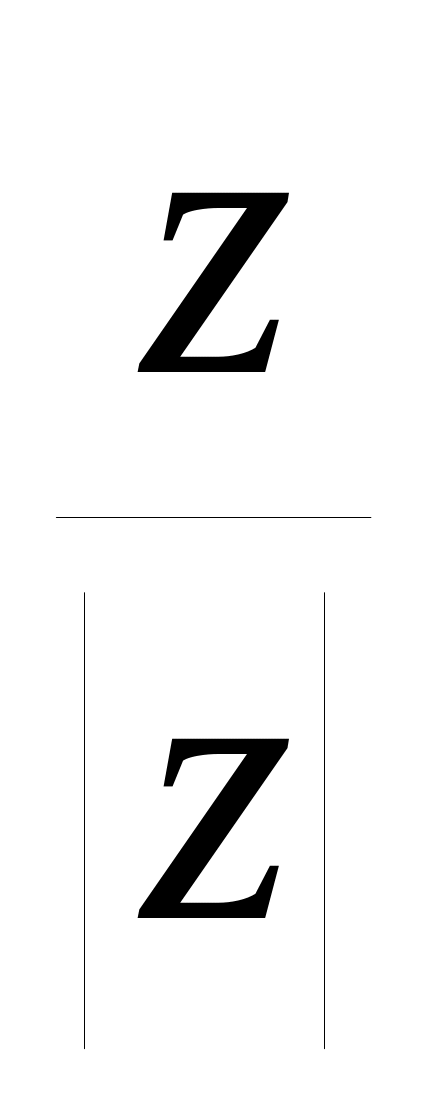6. signum(z) –повертає 0, якщо і в іншому випадку.

1.5 Розв’язування диференціальних рівнянь в середовищі пакету MathCad Розв’язування диференціальних рівнянь 1-го порядку. Розв’язок задачі Коші

При розв’язуванні диференціального рівняння шуканою величиною є функція. MathCAD має ряд вбудованих функцій, призначених для чисельного розв’язання диференціального рівняння. В результаті розв’язання одержується матриця, яка містить значення функції–розв’язку, обчислені на деякій множині точок. При використанні вбудованих функцій, які передбачають різні методи пошуку розв’язку в загальному випадку повинні бути задані такими величинами:

1. Початкові умови;

2. Набір точок, в яких потрібно знайти розв’язок;

3. Саме диференціальне рівняння.

Для розв’язання диференціальних рівнянь першого порядку в MathCAD використовується функція rkfixed(y,x1,x2,n,D), яка використовує метод Рунге-Кутта 4-го порядку.

y – вектор початкових умов розмірності n, де n – порядок диференціального рівняння чи кількість рівнянь у системі. У випадку диференціального рівняння першого порядку вектор початкових умових вироджується в одну точку .

x1, x2 – граничні точки інтервалу, на якому шукається розв’язок диференціального рівняння.

n – кількість точок (не рахуючи початкової), в яких шукається наближений розв’язок. Цей аргумент визначає кількість рядків (n+1) в матриці, яку повертає функція rkfixed.

D(x,y) – вектор-функція перших похідних.