
- •Бабанов в.В. Теоретическая механика, Основы теоретической механики, сопротивления материалов и статики сооружений для архитекторов: Учеб. Для вузов. Т. 2.
- •Глава 11 совместное действие растяжения (сжатия) с изгибом
- •11.1. Определение усилий в статически определимых расчётных
- •11.1.1. Балки и рамы
- •11.1.2. Трёхшарнирные арки
- •Геометрические характеристики сечений трёхшарнирной арки
- •Определение усилий в сечениях трёхшарнирной арки (к примеру 11.3)
- •11.1.3. Комбинированные расчётные схемы
- •11.2. Напряжения при совместном действии растяжения (сжатия) с изгибом
- •11.3. Внецентренное сжатие. Понятие о ядре сечения
- •Контрольные вопросы
- •Глава 12 основные теоремы строительной механики. Определение перемещений
- •12.1. Общие положения
- •12.2. Работа сил. Потенциальная энергия деформации
- •12.3. Принцип возможных перемещений
- •12.4. Основные теоремы строительной механики
- •12.4.1. Теоремы о взаимности возможных работ и взаимности возможных перемещений
- •12.4.2. Теорема о взаимности возможных реакций
- •12.5. Определение перемещений в статически определимых расчётных схемах
- •12.5.1. Перемещения от внешней нагрузки
- •Пощади и центры тяжести простейших геометрических фигур
- •12.5.2. Перемещения от теплового воздействия
- •12.5.3. Перемещения от неравномерной осадки опор и неточности изготовления стержней
- •Контрольные вопросы
- •Глава 13 расчёт статически неопределимых систем методом сил
- •13.1. Свойства статически неопределимых систем.
- •Степень статической неопределимости
- •13.2. Идея метода сил. Система канонических уравнений
- •13.4. Выбор основных систем метода сил. Общая последовательность расчёта
- •Последовательность расчёта методом сил
- •Определение усилий в статически неопределимой ферме
- •13.4. Расчёт при наличии начальных деформаций
- •13.5. Упрощения при расчёте симметричных систем
- •13.6. Понятие о расчёте пространственных рам
- •Контрольные вопросы
- •Глава 14 расчёт статически неопределимых систем методом перемещений
- •14.1. Основные положения. Степень кинематической неопределимости
- •14.2. Идея метода перемещений. Система канонических уравнений и общая последовательность расчёта
- •Последовательность расчёта методом перемещений
- •14.3. Упрощения расчётов при использовании метода перемещений
- •14.3.1. Использование основной системы без постановки линейных связей
- •14.3.2. Учёт симметрии
- •14.4. Понятие о расчёте пространственных рам
- •14.5. Принципы определения перемещений в статически неопределимых системах
- •Контрольные вопросы
- •Глава 15 основы динамики сооружений
- •15.1. Общие положения
- •15.2. Колебания упругих систем с одной степенью свободы
- •15.2.1. Свободные колебания
- •Значения коэффициентов поглощения ψ
- •15.2.2. Вынужденные колебания при действии вибрационной нагрузки
- •15.2.3. Действие ударной нагрузки
- •Приведение равномерно распределённой массы к месту удара
- •15.3. Колебания упругих систем с несколькими степенями свободы
- •15.3.1. Свободные колебания
- •15.3.2. Вынужденные колебания при действии вибрационной нагрузки
- •15.3.3. Учёт симметрии в задачах динамики
- •Меры защиты от динамических воздействий
- •Характеристики физиологического воздействия
- •Контрольные вопросы
- •Глава 16 основы устойчивости сооружений
- •16.1. Основные положения
- •16.2. Устойчивость центрально сжатых прямолинейных стержней
- •Значения критических параметров для центрально сжатых стержней
- •16.3. Применение метода перемещений при расчёте устойчивости плоских рам
- •16.3.1. Общие принципы использования метода
- •16.3.2. Упрощения при расчёте рам на устойчивость
- •16.4. Критические напряжения и пределы применимости формулы Эйлера
- •Значения предельных гибкостей
- •16.5. Практические расчёты на продольный изгиб
- •Контрольные вопросы
- •Глава 17 основы расчёта подпорных стен
- •17.1. Общие понятия
- •Физико – механические характеристики грунтов
- •17.2. Активное и пассивное давления на подпорную стену
- •17.3. Эпюры интенсивности бокового давления
- •1. Многослойность массива сыпучего тела.
- •2. Влияние временной равномерно распределённой нагрузки на поверхности сыпучего массива.
- •17.4. Проверка устойчивости и прочности подпорных стен
- •Расчёт подпорной стены из условия устойчивости на опрокидывание.
- •2. Расчёт подпорной стены из условия устойчивости на сдвиг (скольжение).
- •3. Расчёт подпорной стены из условия прочности.
- •17.5. Понятие о расчёте тонкостенных подпорных стен
- •Контрольные вопросы
- •Приложения
- •Расчётные сопротивление проката для стальных конструкций
- •От единичных смещений связей
- •От внешних воздействий
- •Смещений при расчёте на устойчивость
- •Список использованной литературы
- •Оглавление
- •Глава 11. Совместное действие растяжения (сжатия) с изгибом
- •11.1.1. Балки и рамы
- •Глава 12. Основные теоремы строительной механики. Определение
- •Глава 13. Расчёт статически неопределимых систем методом сил
- •Глава 14. Расчёт статически неопределимых систем методом
- •Глава 15. Основы динамики сооружений
- •Глава 16. Основы устойчивости сооружений
- •Глава 17. Основы расчёта подпорных стен
Определяем перемещение по формуле (12.24).
 (рад),
(рад),
или, подставляя численное значение жёсткости EA,
 рад.
рад.
12.5.2. Перемещения от теплового воздействия
При тепловом воздействии любой материал изменяет свою форму. Поэтому необходимо различать деформации от силового и теплового воздействий.
При силовом воздействии на плоские расчётные схемы имеют место изгиб и растяжение (сжатие) (рис.12.15. а). При тепловом воздействии имеют место искривление и удлинение (укорочение) (рис.12.15, б).
Последние виды деформаций изменяют только форму элемента, но никаких напряжений в расчётных сечениях статически определимых систем не вызывают.
При расчёте на тепловое воздействие учитывается не температура окружающей среды, а её ожидаемое изменение в процессе эксплуатации сооружения.
С целью упрощения инженерных расчётов вводится допущение о линейном характере изменения температуры по высоте сечения элемента. Зная расположение нейтральной оси стержня, можно заданное изменение температуры разложить на два воздействия – на так называемые “равномерный и неравномерный нагрев” (рис. 12.16).
Равномерный
нагрев
характеризуется температурой
![]() на уровне нейтральной оси стержня n
– n
и вызывает
только удлинение или укорочение стержня.
на уровне нейтральной оси стержня n
– n
и вызывает
только удлинение или укорочение стержня.
При этом температура на уровне нейтральной оси в общем случае равна
 ,
(12.31)
,
(12.31)
а когда h1 = h2 = 0,5h,
 .
(12.32)
.
(12.32)
Неравномерный нагрев характеризуется перепадом температур Δt, вызывающей искривление стержня из-за различия в удлинении волокон по высоте сечения стержня.
Рассмотрим деформации бесконечно малого элемента стержня dx (рис.12.17) при тепловом воздействии отдельно для равномерного и неравномерного нагрева.
При действии равномерного нагрева удлинение (укорочение) бесконечно малого элемента стержня будет равно (рис.12.17, а)
![]() ,
(12.33)
,
(12.33)
где αt – коэффициент линейного расширения материала стержня.
При действии неравномерного нагрева основным показателем искривления является угол Δdφt (рис.12.17, б) между боковыми гранями элемента.
Его величину определим следующим образом.
Изменение длины крайних волокон по высоте сечения будет равно:
для нижних
 ;
;для верхних
 .
.
Тогда
![]() ,
,
или, так как (t' – t'') =Δtº (рис.12.16), окончательно получим
![]() .
(12.34)
.
(12.34)
Для получения формулы определения перемещений от теплового воздействия рассмотрим линейно деформируемую расчётную схему (состояние tº) при заданном тепловом воздействии (рис.12.18, а) и вспомогательное состояние k с приложенной единичной силой по направлению искомого перемещения Δkt .
Для состояния k (рис. 12.18, б) применим принцип возможных перемещений (12.15), приняв для него в качестве возможных перемещения состояния tº.
Возможная работа внешних сил равна
Ttk = 1∙ Δkt . (12.35)
Возможная работа внутренних сил для плоской стержневой системы определяется выражением
![]() .
(12.36)
.
(12.36)
Подставив в (12.36) выражения деформаций от теплового воздействия (12.33) и (12.34) и вынося за знаки интегралов постоянные множители, не зависящие от интегрирования, получим
![]()
В полученном выражении величины, стоящие под знаками интегралов, представляют собой площади эпюр Nk и Mk.
Обозначив
![]() и
и
![]() ,
,
получим окончательное выражение для возможной работы внутренних сил
![]() .
(12.37)
.
(12.37)
Подставив (12.35) и (12.37) в (12.15), получим формулу для определения перемещений от температурного воздействия:
![]() .
(12.38)
.
(12.38)
Правило знаков: каждый член формулы (12.38) при вычислении по участкам будет положительным при совпадении характера деформации (растяжения с удлинением или изгиба с искривлением) от единичной силы вспомогательного состояния и теплового воздействия.
Для первого члена формулы (12.38) знак может быть получен автоматически, если при вычислении значения и Nk подставлять со своими знаками.
Пример 12.5. Определить вертикальное перемещение шарнира С и горизонтальное перемещение ригеля, а также построить характер деформированной схемы трёхшарнирной рамы (рис.12.19, а), если тепловому воздействию подвергаются её стойки. Рама изготовлена из двутавра № 45 (h = 0,45 м, коэффициент линейного расширения стали αt = 120∙10-7 1/град.
Решение.
Определяем параметры температурного воздействия:
левая стойка
 =0,5(–45º
+ 15º)
= –15º;
Δt1
= |15º –
(– 45º)|
= 60º;
=0,5(–45º
+ 15º)
= –15º;
Δt1
= |15º –
(– 45º)|
= 60º;правая стойка
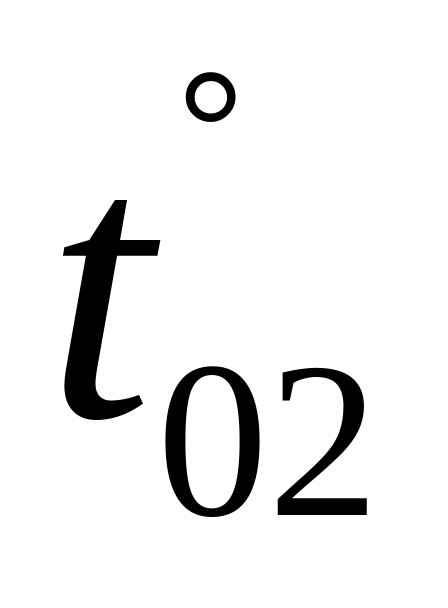 =0,5(45º
+ 150)
= 30º;
Δt2
= |15º –
45º |
= 30º.
=0,5(45º
+ 150)
= 30º;
Δt2
= |15º –
45º |
= 30º.
2. Определяем вертикальное перемещение шарнира С.
Для этого производим расчёт вспомогательного состояния1(рис.12.19, б) от единичной силы, приложенной по направлению искомого перемещения, т.е. определяем опорные реакции и строим эпюры N1 и M1.
Значение перемещения определяем по формуле (12.38), производя запись вычислений по участкам:
![]()
 +
+![]() =
=
(левая стойка) (правая стойка)
= – 517,5αt = – 517,5∙120∙10-7 = – 0,62∙10-2 м.
Определяем горизонтальное перемещение ригеля рамы.
Так как ригель рамы не испытывает теплового воздействия, то продольными деформациями в его сечениях при определении перемещений пренебрегаем.
Для определения искомого перемещения рассматриваем вспомогательное состояние 2 (рис.12.19, в), для которого определяем опорные реакции и строим эпюры N2 и M2.
Значение перемещения определяем по формуле (12.38), производя запись вычислений по участкам:
![]() +
+![]() =
=
(левая стойка) (правая стойка)
= 1057,5αt = 1057,5∙120∙10-7 = 1,269∙10-2 м.
Производим построение деформированной схемы рамы.
При построении характера деформированной схемы рамы определим продольные деформации левой и правой стоек, подвергающихся тепловому воздействию:
левая стойка
 =
120∙10-7∙(–
15º)∙4,5
= – 0,081∙10-2
м;
=
120∙10-7∙(–
15º)∙4,5
= – 0,081∙10-2
м;правая стойка
 =
120∙10-7∙30º
∙4,5
= 0,162∙10-2
м.
=
120∙10-7∙30º
∙4,5
= 0,162∙10-2
м.
Таким образом, левая стойка при заданном тепловом воздействии укорачивается, а правая – удлиняется.
Имея значения узловых перемещений рамы и зная характер искривления от теплового воздействия левой и правой стоек, можем построить характер деформированной схемы (рис.12.19, г).
12.5.3. Перемещения от неравномерной осадки опор и неточности изготовления стержней
Для получения формулы определения перемещений, возникающих при неравномерной осадке опор, рассмотрим линейно деформируемую расчётную схему (состояние Δ) при заданных смещениях опорных связей (рис.12.20, а) и вспомогательное состояние k (рис. 12.20, б) с приложенной единичной силой по направлению искомого перемещения ΔkΔ .
Для состояния k применим принцип возможных перемещений (12.15), приняв для него в качестве возможных перемещения состояния Δ.
Возможная работа внешних сил равна
TΔk = 1∙ΔkΔ + R1∙Δ1 + R2∙Δ2 +…+ Ri∙Δi +…+ Rn∙Δn =1∙ΔΔt +∑ Ri∙Δi.
Так как при неравномерной осадке опор в стержнях заданной расчётной схемы усилий и соответствующих им деформаций не возникает, то работа внутренних сил WΔk = 0. Поэтому на основании (12.15) имеем, что TΔk = 0, откуда находим, что
ΔkΔ = – ∑Ri∙Δi. (12.39)
В формуле (12.39) произведение под знаком суммы представляет собой возможную работу, потому знак произведения определяется по тому, совпадает направление Ri∙с направлением Δi. При совпадении знак произведения положителен, при несовпадении – отрицателен.
Вывод формулы для определения перемещений, вызванных неточностью изготовления стержней аналогичен предыдущему, и сама формула имеет вид:
ΔkΔ = ∑Ni∙Δi, (12.40)
где Ni– усилие в неточно изготовленном стержне по вспомогательному состоянию ;
Δi – величина неточности изготовления стержня.
В формуле (12.40) перед знаком суммы в отличие от (12.39) отсутствует знак минус, так как работа внутренних сил отрицательна.
Правило знаков для произведения определяется, как и в (12.39), по знаку возможной работы: при совпадении направлений – знак “плюс”, при несовпадении – знак “минус”.
Пример 12.6. Определить угол поворота сечения K консоли шарнирно- консольной балки при указанном смещении опор (рис.12.21, а) и построить характер деформированной схемы.
Решение.
1. Во вспомогательном состоянии (рис.12.21, б) прикладываем единичный момент в сечении K и определяем реакции во всех смещаемых связях.
2. Используя формулу (12.39), определяем угол поворота
φK = Δ1Δ = – (0,05∙0,06 – 0,125∙0,08 – 0,375∙0,04 + 0,25∙0,02) = – 0,01 рад.
Характер деформированной схемы балки показан на рис.12.21, в. Деформированная схема построена по известным смещениям опор.
Пример 12.7. Определить изменение расстояния между опорами А и B рамы (рис.12.22, а), если её затяжка изготовлена короче проектной на величину 0,06 м.
Решение.
Вспомогательное состояние для определения перемещения показано на рис. 12.22, б. Так как опорная точка А неподвижна, то для определения изменения расстояния между А и В достаточно определить горизонтальное перемещение опоры В.
Усилие в затяжке дл вспомогательного состояния N1 = 2.
Согласно (12.40) перемещение опоры B будет
ΔВ = Δ1Δ = 2∙(– 0,06) = – 0,12 м.
Деформационная схема рамы при данных перемещениях показана на рис.12.22, в.
Контрольные вопросы
Какие перемещения упругих систем называют действительными, а какие – возможными?
Что понимают под действительной и возможной работой силы?
В чем различие в вычислениях действительной и возможной работ?
Покажите связь между работой внешних и внутренних сил упругой системы.
Сформулируйте принцип возможных перемещений.
Сформулируйте теоремы о взаимности возможных работ, о взаимности возможных перемещений и взаимности возможных реакций.
Какой вид имеет формула определения перемещений (Максвелла-Мора) для определения перемещений в плоских упругих расчетных схемах?
Какой вид принимает формула Максвелла-Мора при определении перемещений, если все стержни расчетной схемы работают в условиях изгиба и имеют постоянные сечения по длине?
Какой вид принимает формула Максвелла−Мора при определении перемещений в фермах?
Какой вид принимает формула Максвелла−Мора при определении перемещений в комбинированных расчетных схемах?
Какой вид имеет формула определения перемещений (Максвелла−Мора) для определения перемещений в пространственных упругих расчетных схемах?
Какие состояния упругой системы необходимо рассмотреть для определения перемещений по формуле Максвелла−Мора?
Как определяется вспомогательное состояние упругой системы в зависимости от вида определяемого перемещения?
Какие практические способы используют при определении перемещений по формуле Максвелла−Мора?
В чем состоит способ Верещагина?
Какие формулы перемножения эпюр Вы знаете?
Какие деформации могут возникать в стержнях расчетной схемы при тепловом воздействии, и каким видам указанного воздействия они соответствуют?
Запишите определения перемещений в плоской расчетной схеме при тепловом воздействии.
Как определяются перемещения, вызванные неравномерной осадкой опор и неточностью изготовления стержней?
Вызывает ли деформации стержней расчетной схемы неравномерная осадка опор?
Глава 13 расчёт статически неопределимых систем методом сил
13.1. Свойства статически неопределимых систем.
Степень статической неопределимости
Как было указано в подразд. 3.1 тома I, к статически неопределимым системам относятся такие расчётные схемы, в которых при действии произвольной нагрузки не все реакции и внутренние силы могут быть определены из уравнений равновесия, т.е. такие системы, которые содержат избыточное для обеспечения геометрической неизменяемости системы число связей.
Следовательно, число избыточных связей, удаление которых превращает систему в статически определимую и оставляет геометрически неизменяемой, называется степенью статической неопределимости.
Таким образом, степень статической неопределимости nc связана со степенью свободы расчётной схемы W (см. подразд. 1.5, т.1) зависимостью:
nc = – W. (13.1)
Для плоских расчётных схем на основании зависимости (13.1) и формулы (1.2) степень статической неопределимости может быть определена по формуле:
nc = (Соп – 2Ш) – Д = C – 3Д. (13.2)
Формула (13.2) имеет чётко выраженный статический смысл. Действительно, для каждого диска расчётной схемы можно составить три уравнения равновесия. Следовательно, если расчётная схема содержит Д дисков, то общее число уравнений равновесия будет 3Д. Величина С – число связей, реакции в которых подлежат определению, и при С > 3Д расчётная схема будет статически неопределима столько раз, какова разница между указанными величинами.
В расчётных схемах, содержащих жёсткие соединения отдельных дисков, образующих на плоскости замкнутые контуры, вместо (1.2) используют общую зависимость (1.1), что не всегда удобно. Для практических расчётов используют другую формулу, пригодную для любых рамных и балочных систем, а именно
nc = 3K – Ш, (13.3)
где K – число замкнутых контуров расчётной схемы (в том числе, между расчётной схемой и основанием;
Ш – число простых шарниров (или связей, недостающих до полного защемления) расчётной схемы.
Статический смысл формулы (13.3) состоит в следующем. Любой бесшарнирный замкнутый контур является трижды статически неопределимым (рис.13.1, а). Постановка (“врезка”) одного простого шарнира удаляет одну связь, т.е. понижает степень статической неопределимости на единицу (рис. 13.1, б), “врезка” lдвух шарниров (рис. 13.1, в) удаляет две связи, а “врезка” трех шарниров делает контур статически определимым (рис. 13.1, д). Таким образом, в формуле (13.2) 3K – степень статической неопределимости расчётной схемы в предположении, что в ней полностью отсутствуют шарниры (все связи – полное защемление), а Ш – на какую величину понижена степень статической неопределимости из-за наличия шарниров.
Применение формул (13.2) и (13.3) покажем на примере рамы, изображённой на рис. 13.2, а.
Использование формулы (13.2).
Число опорных связей Соп = 5. Для определения числа шарниров удалим опорные связи (на рис. 13.2, б они условно показаны пунктирными линиями). Тогда, в узле E: Ш =1, в узле С: Ш =2 и в узле D: Ш =1. Итого, число простых шарниров Ш = 4. Число дисков Д = 3.
Следовательно, nc = (5 + 2∙4) – 3∙3 = 4.
2. Использование формулы (13.3).
Для облегчения использования формулы (13.3) покажем в узле C (рис. 13.2, в) раздельно шарниры, соединяющие диски расчётной схемы, и линейную опорную связь; в узле D шарнирно неподвижную опору изобразим в виде примыкающего к основанию кратного шарнира (что одно и то же). Кроме этого, обозначим все части плоскости на расчётной схеме, окружённые со всех сторон дисками и основанием (замкнутые контуры).
Таким образом, число замкнутых контуров K = 5, число простых шарниров Ш = 11. Получение последней цифры рассмотрим подробнее по узлам.
Узел А. Имеет шарнирно подвижную опору. Следовательно, число связей, недостающих до полного защемления Ш = 2.
Узел. Е. Ш = 1, простой шарнир, соединяющий два диска.
Узел С. Имеет два простых шарнира, соединяющие три диска схемы, и две связи, недостающие до полного защемления в шарнирно подвижной опоре.
Узел D. Имеет два примыкающих к основанию шарнира.
Узел F. Ш =1 по аналогии с узлом А.
Итого по всем узлам расчётной схемы Ш = 2 + 1 + 4 + 2 + 2 = 11.
Следовательно, nc = 3∙5 – 11 = 4.
Примечание. Определение числа простых шарниров в узлах со сквозными и примыкающими шарнирами см. подразд. 1.3.1. т.1 и рис. 1.7 и 1.8.
Степень статической неопределимости ферм на основании (1.6) и (13.1) определяется по формуле
nc = (Cоп + Сф) – 2У = С – 2У. (13.4)
Формула (13.4) также, как и предыдущие, имеет чётко выраженный статический смысл. В этом случае С – число опорных реакций и усилий в стержнях фермы, подлежащих определению, а 2У – число уравнений равновесия, которые можно составить для всех узлов фермы, включая опорные. Разница между этими величинами и даёт степень статической неопределимости.
В зависимости от образования расчётной схемы можно различать внешне статически неопределимые и внутренне статически неопределимые системы, хотя, как выяснится из дальнейшего, это разделение является условным.
Внешне статически неопределимой называют такую систему, которая имеет в качестве избыточных только внешние связи, т.е. лишние опорные закрепления. Примером такой системы может служить рама, изображённая на рис. 13.3, а. Жёсткое соединение всех стержней рамы представляет собой один диск, для прикрепления которого к основанию достаточно трёх связей. Рама имеет восемь опорных связей: три – в опоре А, по две – в опорах B и C и одну – в опоре D, т.е. пять связей – избыточные, и рама пять раз статически неопределима.
Внутренне статически неопределимой называют такую систему, которая имеет минимально необходимое число опорных связей, а все избыточные связи принадлежат соединениям внутренних элементов расчётной схемы. На рис.13.3, б изображены трижды статически неопределимые рамы, прикреплённые к основанию только тремя связями, т.е. внешние связи в этих рамах не могут являться избыточными.
Отметим основные свойства статически неопределимых систем:
1. Статически неопределимые системы по сравнению со статически определимыми более жёсткие, т.е. при одинаковых нагрузках перемещения в них значительно меньше.
2. В расчётных сечениях элементов статически неопределимой системы усилия меньше, чем в статически определимых при той же нагрузке.
На рис. 13.4 а и б показаны трёхпролётная шарнирно-консольная балка и неразрезная балка с таким же числом пролётов. Обе балки загружены одинаковой нагрузкой в первом пролёте. Наибольшим изгибающим моментов в шарнирно-консольной балке является Mб, действующий в сечении, где приложена сила F. В том же сечении неразрезной балки расчётный изгибающий момент Mр < Mб. Аналогичное сравнение прогиба балок в точке приложения силы показывает, что Δ2 <Δ1.
3. Статически неопределимые системы обладают распределительной способностью: локальная нагрузка вызывает появление усилий во всех сечениях расчётной схемы, значения которых уменьшаются по мере удаления от места приложения нагрузки. В статически определимых системах локальная нагрузка может вызвать лишь локальное появление усилий (сравните эпюры M на рис. 13.4 а и б).
4. Статически неопределимые системы более надёжны, нежели статически определимые: выход из строя одного из элементов расчётной схемы ещё не исчерпывает их несущей способности и при определённых условиях не приводит к обрушению.
Например, удаление опорной связи D в неразрезной балке (рис.13.4, в) не приводит к обрушению конструкции, в то время как удаление такой же связи в шарнирно-консольной балке приводит к мгновенной изменяемости части расчётноё схемы.
5. Статически неопределимые конструкции проще в изготовлении и просты в эксплуатации, так как конструкция любого шарнира сложнее, чем жёсткое соединение.
6. При наличии начальных деформаций (тепловое воздействие, неравномерная осадка опор и неточность изготовления элементов конструкции) в статически неопределимых системах возникают усилия из-за наличия избыточных связей, препятствующих свободному развитию этих деформаций. Возникающие при этом усилия прямо пропорциональны жёсткости элементов статически неопределимой системы.
На рис. 13.5 а и б показаны примеры однопролётных балок, статически определимых и статически неопределимых при действии осадки опор и тепловом воздействии.
7. Статически неопределимые конструкции, как правило, более экономичные, нежели статически определимые, во-первых, за счёт меньших размеров поперечных сечений; во-вторых, за счёт изготовления.
13.2. Идея метода сил. Система канонических уравнений
Метод сил широко применяется для расчёта разнообразных плоских и пространственных систем и является основанием для многих приближённых методов.
Для описания идеи метода рассмотрим простейшую расчётную схему – неразрезную двухпролётную балку, загруженную произвольной нагрузкой (рис.13.6, а). Данная расчётная схема является дважды статически неопределимой.
Удалим опорные связи в точках A и B и заменим их действием неизвестными реакциями X1 и X2 (рис.13.6, б). Полученная таким образом расчётная схема является статически определимой, так удалено две избыточные связи (по степени статической неопределимости). Её называют основной системой метода сил.
Для полученной основной системы воспользуемся принципом независимости действия сил и рассмотрим следующие воздействия: состояние 1 от действия силы X1 (рис.13.6, в); состояние 2 от действия силы X2 (рис.13.6, г) и состояние F от действия внешней нагрузки (рис.13.6, д).
Во всех перечисленных состояниях точки А и B вследствие деформаций основной системы получат перемещения по направлению удалённых связей, сумма которых по каждому из указанных направлений даст полные перемещения
ΔA =Δ11 + Δ12 + Δ1F;
ΔB =Δ21 + Δ22 + Δ2F .
Чтобы основная система соответствовала по своим деформациям заданной расчётной схеме, очевидно, необходимо выполнения условий
 ΔA
= 0; ΔB
= 0
ΔA
= 0; ΔB
= 0
и
(13.5)
Δ21 + Δ22 + Δ2F = 0 .
Для выражения перемещений, входящих в (13.5) воспользуемся зависимостью (12.1) и запишем
Δ11 = δ11X1; Δ12 = δ12X2; Δ21 = δ21X1; Δ22 = δ22X2.
П одставив эти выражения в (13.5), получим
(13.6)
δ21X1 + δ22X2 + Δ2F = 0.
Запись (13.6) называется системой канонических уравнений метода сил.
Как и (13.5), система канонических уравнений имеет следующий геометрический смысл: сумма перемещений по направлению удалённых связей от действия реакций в этих связях и внешнего воздействия равна нулю.
Приведённый вывод системы канонических уравнений справедлив для любой расчётной схемы с любой степенью статической неопределимости. Поэтому, если степень статической неопределимости nc = n, то система канонических уравнений будет иметь вид:
 δ11X1
+ δ12X2
+ …+ δ1iXi
+…+ δ1nXn
+Δ1F
= 0;
δ11X1
+ δ12X2
+ …+ δ1iXi
+…+ δ1nXn
+Δ1F
= 0;
δ21X1 + δ22X2 + …+ δ2iXi +…+ δ2nXn +Δ2F = 0; (13.7)
……………………………………………….
δn1X1 + δn2X2 + …+ δniXi +…+ δnnXn +ΔnF = 0.
В системе канонических уравнений (13.7) коэффициенты при неизвестных с одинаковыми индексами называются главными коэффициентами податливости и они всегда положительны δii > 0. Остальные коэффициенты называются побочными, и для них выполняется теорема о взаимности возможных перемещений δik = δki.
Любой коэффициент системы канонических уравнений δik, согласно (12.18), есть возможное перемещение по направлению удалённой связи i от действия единичной безразмерной силы, приложенной по направлению удалённой связи k.
Размерности коэффициентов при неизвестных и свободных членов системы канонических уравнений легко определяются на основании их геометрического смысла, сформулированного выше.
Так, для неразрезной балки, использованной при выводе системы канонических уравнений (рис.13,6, а), неизвестными метода сил являются сосредоточенные силы (единицы измерения – кН), перемещения по направлению этих сил будут линейными (единицы измерения – м). Следовательно, свободные члены системы уравнений, являющиеся перемещениями в статически определимой основной системе, будут измеряться в м, а все коэффициенты при неизвестных – в м/кН.
Если бы для той же балки была выбрана другая основная система (рис.13.7), в которой удалена одна линейная связь, а вторая – угловая, то, рассуждая аналогично получим нижеследующее.
В направлении первого неизвестного отрицается сумма линейных перемещений, измеряемых в м. Так как X1 измеряется в кН, а X2 – в кН·м, то единицами измерения коэффициентов при неизвестных первого уравнения будут: для δ11 – м/кН, для δ12 – м/кН∙м (1/кН), а для свободного члена Δ1F – м.
Аналогично, второе уравнение отрицает в направлении второго неизвестного сумму угловых перемещений, измеряемых в рад. Значит, для второго уравнения единицами измерения коэффициентов при неизвестных будут: для δ21 – рад/кН, для δ22– рад/кН∙м, а для Δ2F – рад.
Коэффициенты при неизвестных и свободные члены системы канонических уравнений определяются как перемещения в статически определимых системах в зависимости от типа расчётной схемы по формулам (12.23), (12.24) или (12.25).
Для определения
коэффициентов при неизвестных и свободных
членов системы канонических уравнений
в основной системе метода сил необходимо
определить усилия от единичных сил,
последовательно прикладываемых по
направлению удалённых связей (по
направлению неизвестных), т.е. построить
эпюры усилий
![]() –
при расчёте балок и рам,
–
при расчёте балок и рам,![]() – при расчёте ферм и
,
–
при расчёте комбинированных систем
(при i
= 1…n=nc),
а также построить, соответственно, эпюры
усилий от действующих нагрузок –
– при расчёте ферм и
,
–
при расчёте комбинированных систем
(при i
= 1…n=nc),
а также построить, соответственно, эпюры
усилий от действующих нагрузок –
![]() ,
,![]() .
.
Здесь и далее верхним индексом “0” будем обозначать эпюры усилий в основной системе.
В силу равенства δik = δki матрица коэффициентов при неизвестных получается симметричной, является положительно определённой, и её определитель не равен нулю. Поэтому система уравнений для каждого варианта загружения имеет одно единственное решение, которое по правилу Г.Крамера можно получить как
![]() ,
,
где Xi
– искомое неизвестное;
![]() – определитель матрицы коэффициентов
при неизвестных;
– определитель матрицы коэффициентов
при неизвестных;
![]() – тот же определитель, в котором i
– ый столбец заменён столбцом
свободных членов.
– тот же определитель, в котором i
– ый столбец заменён столбцом
свободных членов.
После определения неизвестных Xi задачу можно считать решённой. Используя эпюры усилий единичных сил, приложенных в основной системе на стадии получения системы канонических уравнений в численном виде на основании принципа независимости действия сил можно определить усилия заданной расчётной схеме как сумму усилий от Xi и внешней нагрузки:
для балок и рам
![]() ;
(13.8)
;
(13.8)
для ферм
![]() ;
(13.9)
;
(13.9)
для комбинированных систем
; (13.10)
.
13.4. Выбор основных систем метода сил. Общая последовательность расчёта
Как было отмечено в предыдущем параграфе, основной системой метода сил будем называть геометрически неизменяемую статически определимую систему, полученную из заданной статически неопределимой путём удаления избыточных связей.
При получении основной системы могут удаляться как внешние связи, так и внутренние, или их комбинации. Получение основной системы метода сил предполагает многовариантность, так как для любой статически неопределимой системы можно, в принципе, предложить сколь угодно много основных систем. Поэтому неизбежно встаёт вопрос о выборе основной системы с точки зрения её рациональности для данной расчётной схемы и действующей на неё нагрузкой.
Рациональность выбора предполагает следующие требования к основной системе:
Основная система должна быть проста для расчёта.
Коэффициенты при неизвестных системы канонических уравнений метода сил и свободные члены, полученные на основе выбранной основной системы должны быть, по возможности, одного порядка. Различие коэффициентов системы алгебраических уравнений на несколько порядков обычно приводит к ухудшению её обусловленности и, как следствие, к ошибочным результатам расчёта.
Выбранная основная система должна давать возможность получить как можно больше нулевых значений побочных коэффициентов при неизвестных и свободных членов системы уравнений. Это позволяет упростить решение этой системы и получить более точный результат.
Естественно, эти требования относятся, главным образом, к системе с большой степенью статической неопределимости. При nc ≤ 3 наиболее важным является первое требование.
Рассмотрим несколько примеров выбора основных систем для плоских стержневых систем.
1. Статически неопределимые однопролётные балки (рис. 13.8, а и 13.9, а).
Основная система может быть выбрана путём удаления линейных связей на одной из опор, т.е. основная система будет представлять собой консольную балку (рис. 13.8, в и 13.9, в), или удалением связей, препятствующих повороту в защемлениях (рис.13.8, б и 13.9, б). Второй вариант предпочтительнее, так как в грузовом состоянии основной системы эпюры изгибающих моментов по концам балок будут иметь нулевые значения, что облегчает счёт.
Неразрезная балка (рис. 13.10, а).
Основная система может быть получена удалением промежуточных опор балки (рис.13.10, б), удалением угловых связей (врезкой шарниров) над каждой промежуточной опорой (рис.13.10, в) и комбинацией этих двух приёмов (рис. 13.10, г). Рациональным для неразрезной балки является вариант, изображённый на рис.13.10, в. В этом случае каждый пролёт балки в основной системе работает как простая балка и независимо от других пролётов, что приводит к простым эпюрам изгибающих моментов и простоте вычисления как коэффициентов при неизвестных, так и свободных членов. Кроме того, при любом количестве неизвестных метода сил каждое из уравнений системы будет содержать не более тёх неизвестных из-за равенства нулю побочных коэффициентов.
П- образная рама (рис.13.11, а).
Для трижды статически неопределимой рамы показаны шесть вариантов основной системы (рис.13.11, б – ж), из которых наиболее рациональными являются основные системы, изображённые на рис.13.11, е и ж. В первом случае основная система после удаления связей превращена в трёхшарнирную раму, во втором – в балочную систему, в которой два стержня (левая стойка и ригель рамы) при отсутствии поперечных нагрузок будут нулевыми, а при их наличии будут работать как простые балки.
Основные системы, приведённые на рис.13.11, и и з, являются примерами неправильного удаления связей.
В основной системе, показанной на рис.13.11, и удалены: угловая связь в правой опоре (получили шарнирно неподвижную опору), в правой опоре – угловая и вертикальная линейная связи. В результате оставшиеся линейные связи (две в левой опоре и одна горизонтальная в правой) имеют общую точку пересечения – мгновенный центр вращения, вокруг которого и произойдёт бесконечно малый поворот расчётной схемы.
В основной системе, показанной на рис.13.11, з удалены три угловые связи в сечениях ригеля рамы, в результате чего врезанных шарнира оказались расположены на одной прямой.
4. Двухпролётная одноэтажная рама (рис.13.12, а). Для рамы показаны два возможных варианта основной системы (рис. 13.12, б и в) и изменяемая основная система (рис. 13.12, г), имеющая мгновенный центр вращения точку О.
5. Рама с несмещающимися узлами (несвободная рама) (рис.13.13, а).
Для рамы показаны три варианта основной системы (рис.13.13, б – г), из которых последняя является наиболее рациональной. Эта основная система получена врезкой сквозных шарниров во все узлы рамы, в результате чего заданная расчётная схема превращена в шарнирную (ферму), в которой каждый стержень работает как простая балка. На рис. 13.13, д показана основная система с неприемлемым вариантом удаления связей: в левом защемлении кроме угловой связи удалена горизонтальная линейная связь; в стойке удалена угловая связь в верхнем её сечении, в результате чего вся стойка, из-за наличия опорного шарнира стала представлять собой вертикальную линейную связь. В результате верхний диск (ригель) оказался прикреплённым к основанию тремя параллельными вертикальными связями, что недопустимо.
6. Однопролётная рама с затяжкой (рис.13.14, а).
Основная система может быть получена удалением горизонтальной связи в одной из опор рамы и затяжки, в результате чего получается балка с осью ломаного очертания (рис.13.14, б); врезкой шарнира в ригеле и удалением затяжки, в результате основная система принимает вид трёхшарнирной рамы (рис. 13.14, в); удалением горизонтальной связи в одной из опор и врезкой шарнира в ригеле, результат – распорная рама с затяжкой (рис.13.14, г). Недопустимый вариант показан на рис.13.14, д, где удалена горизонтальная линейная связь в правой опоре, а шарнир врезан в узел на уровне затяжки. В результате имеющийся в расчётной схеме замкнутый контур остался статически неопределимым (в контуре по его обходу всего два шарнира вместо необходимых трёх), а стойка рамы ниже врезанного шарнира стала геометрически изменяемой частью схемы (три шарнира на одной прямой).
7. Балочный замкнутый контур (рис.13.15, а).
Данная расчётная схема имеет минимально необходимое число внешних связей, из которых ни одна не может быть удалена (рис.13.15, г). Расчётная схема имеет внутреннюю статическую неопределимость, поэтому основная система может быть получена удалением только внутренних связей (рис.13.15, б – г). В случае удаления хотя бы одной внешней связи (рис. 13.15, д) схема превращается в механизм.
8. Балочная ферма (рис. 13.16, а).
Данная расчётная схема, как и предыдущая, является внутренне статически неопределимой. Статическая неопределимость (nc =1) обусловлена наличием избыточного стержня во второй панели фермы. Поэтому основная системы может быть получена удалением одного из стержней именно в этой панели (рис.13.16, б и в). Недопустимость удаления других стержней фермы показа на рис.13.16, г, в результате чего вторая панель остаётся статически неопределимой частью расчётной схемы, а вся схема превращается в механизм.
9. Двухпролетная балочная ферма (13.17, а).
Основная система может быть выбрана как удалением одной из вертикальных опорных связей (рис.13.17, б), так и удалением стержня фермы (рис.13.17, в). Второй вариант предпочтительнее, так как в этом случае основная система представляет собой две отдельно работающие балочные фермы, и при загружении одной их них, в стержнях второй фермы не будет возникать никаких усилий.
Приведённые выше примеры не исчерпывают всего многообразия приёмов при выборе основных систем метода сил для различных статически неопределимых расчётных схем, они лишь дают представления, каким образом могут быть удалены избыточные связи, и как получить наиболее рациональную основную систему.
Общая последовательность расчёта методом сил приведена в таблице 13.1.
Таблица 13.1
Последовательность расчёта методом сил
№ п.п. |
Балки и рамы |
Комбинированные системы |
Фермы |
|
1 |
Определить степень статической неопределимости |
|||
nc = 3К – Ш |
nc = 3К – Ш |
nc = C – 2У |
||
2 |
Записать систему канонических уравнений в общем виде |
|||
3 |
Выбрать основную систему метода сил |
|||
4 |
Построить эпюры усилий в основной системе от последовательного приложения единичных сил по направлению удалённых связей |
|||
(при i = 1…n) |
, (при i = 1…n) |
(при i = 1…n) |
||
5 |
Построить эпюры усилий в основной системе от заданной нагрузки
|
|||
|
, |
|
||
6 |
Определить коэффициенты при неизвестных системы канонических уравнений |
|||
|
|
|
||
7 |
Определить свободные члены системы канонических уравнений |
|||
8 |
|
|
|
|
Окончание табл. 13.1 |
||||
9 |
Записать систему канонических уравнений и из её решения определить значения неизвестных Xi. |
|||
10 |
Построить эпюры усилий в заданной расчётной схеме |
|||
|
;
|
|
||
11 |
Произвести деформационную проверку расчета |
|||
либо
где
|
либо
где ;
|
либо
где
|
||
|
|
|
Расчёт окончен |
|
12 |
Определить на
основании дифференциальной зависимости
|
|||
13 |
Из условия равновесия узлов определить продольные силы во всех стержнях и построить эпюру NF |
|||
14 |
Произвести статические проверки равновесия: при правильно произведённом расчёте любая отсечённая часть схемы или вся схема, отсечённая от опор, под действием внутренних и внешних сил должна удовлетворять условиям равновесия. |
|||
Примечание. m – число участков интегрирования при изгибе; Сф – число стержней фермы. |
||||
Как видно из этой таблицы общая последовательность расчёта не зависит от типа расчётной схемы. Различия появляются лишь при определении коэффициентов при неизвестных и свободных членов по формуле максвелла – Мора.
При выполнении расчёта необходимо обратить внимание на следующие пункты табл.13.1.
Выполнение деформационной проверки расчёта (см. п.6 табл.13.1).
Смысл деформационной
проверки такой же, как и у системы
канонических уравнений: она
отрицает перемещения в заданной расчётной
схеме по направлению удалённых связей.
Для того, чтобы деформационная проверка
была более корректной, желательно
выбрать новую основную систему метода
сил и построить в ней эпюры усилий от
единичных сил, приложенных по
направлениям удалённых связей
![]() ,
,
![]() и их суммарные эпюры
и их суммарные эпюры
![]() ,
,
![]() .
В связи с этим деформационные проверки
могут быть локальными (использование
эпюр
,
)
или общими (использование эпюр
,
).
Оценка погрешности расчёта производится
по сравнению сумм положительных и
отрицательных величин вычисленных
интегралов и не должна превышать 1%.
.
В связи с этим деформационные проверки
могут быть локальными (использование
эпюр
,
)
или общими (использование эпюр
,
).
Оценка погрешности расчёта производится
по сравнению сумм положительных и
отрицательных величин вычисленных
интегралов и не должна превышать 1%.
2. Построение эпюры поперечных сил (см. п.12 табл.13.1).
Определение поперечных сил на участках с прямолинейной эпюрой изгибающих моментов (рис.13.18) производят на основании правил изложенных в подразд. 10.2 (см. рис.10.11). Для горизонтально ориентированного стержня при выполнении принятого ранее (рис. 10.4) правила знаков для изгибающих моментов можем записать
![]() .
(13.11)
.
(13.11)
Для участков, где действует равномерно распределённая нагрузка, фигуру эпюры изгибающих моментов можно разложить на две составляющие (рис.13.19): прямолинейную и “балочную”, и для каждой из них построить эпюры поперечных сил, а результаты сложить. В силу того, что на рассматриваемом участке эпюра поперечных сил должна быть прямолинейной, ординаты эпюры поперечных сил по концам участка можно записать как
![]() и
и
![]() .(13.12)
.(13.12)
Для вертикальных и наклонных стержней расчётной схемы “верх” и “низ” рассматриваемого участка выбирается произвольно.
Рассмотрим несколько примеров расчёта статически неопределимых систем методом сил при действии внешней нагрузки.
Пример.13.1. Рассчитать неразрезную балку (рис.13.20, а).
Решение.
Степень статической неопределимости при K =2, Ш = 4
nc = 3∙2 – 4 = 2.
2. Система канонических уравнений
δ11X1 + δ12X2 + Δ1F = 0;
δ21X1 + δ22X2 + Δ2F = 0.
3. Выбранная основная система показана на рис.13.20, б.
4. Определяем усилия
в основной системе от единичных моментов,
последовательно прикладываемых по
направлению удалённых связей (рис.13.20,
в
и г),
т.е. построим эпюры
![]() и
и
![]() .
Кроме этого, воспользуемся простотой
задачи и построим деформированные схемы
основной системы от единичных
воздействий, на которых покажем возможные
перемещения, представляющие собой
коэффициенты при неизвестных канонических
уравнений.
.
Кроме этого, воспользуемся простотой
задачи и построим деформированные схемы
основной системы от единичных
воздействий, на которых покажем возможные
перемещения, представляющие собой
коэффициенты при неизвестных канонических
уравнений.
5. Определяем усилия в основной системе от действия заданной нагрузки и строим эпюру (рис.13.20, д). Здесь также покажем перемещения по направлению удалённых связей, представляющие собой свободные члены канонических уравнений.
6. Определяем коэффициенты при неизвестных канонических уравнений.
![]() (рад/кН·м);
(рад/кН·м);
![]() (рад/кН·м);
(рад/кН·м);
![]() (рад/кН·м).
(рад/кН·м).
7. Определяем свободные члены канонических уравнений.
![]() (рад);
(рад);
![]() (рад).
(рад).
8. Производим решение системы канонических уравнений:

Упростим полученную систему уравнений, умножив все его члены на 1,5EI:
2X1 + X2 + 128 = 0,
X1 + 5X2 + 82 = 0.
Используя правило Г.Крамера, получим
![]() ;
;
![]() ;
;
![]() ,
,
откуда
![]()
9. Строим эпюру изгибающих моментов в заданной расчётной схеме
![]() .
.
Эпюра MF показана на рис.13.21, а. Для неразрезных балок указанное сложение производится достаточно просто: необходимо отложить на опорах найденные значения неизвестных и к полученной эпюре опорных изгибающих моментов “подвесить” эпюру .
10. Производим деформационную проверку расчёта. Для этого выбираем новую основную систему (рис.13.21, б), в которой прикладываем сразу все единичные силы по направлению удалённых линейных связей и от их действия строим эпюру . Сравнивая полученную эпюру с эпюрами и , использованными в расчёте, видим, что она им не подобна, т.е. производимая проверка будет достаточно корректна.
![]() =
=
=![]() ,
т.е. проверка
выполнена.
,
т.е. проверка
выполнена.
11. Производим построение эпюры QF на основании дифференциальной зависимости по участкам расчётной схемы.
Участок 1 – левый пролёт балки. Пролёт загружен равномерно распределённой нагрузкой, поэтому для нахождения значений поперечных сил по концам участка используем приём, приведённый на рис.13.19 и описанный формулой (13.12)
![]() ;
;
![]() .
.
Участок 2 – правый пролёт балки. Нагрузка в пролёте отсутствует, эпюра изгибающих моментов очерчена по наклонной прямой. Следовательно, поперечная сила по всему пролёту постоянна. Её значение вычисляем по формуле (13.11)
![]() .
.
Участок 3 – консоль балки.
Q = ∑Fправ = 15,333 кН.
Построенная по полученным значениям эпюра QF показана на рис.13.21, а.
В левом пролёте эпюра QF имеет нулевое значение на расстоянии x0 от левой опоры. Находим экстремальное значение изгибающего момента в этом сечении (рис. 13..21, в).
Q0 = ∑Fлев = 39,25 – 8∙ x0 = 0, x0 = 4,97 м.
Mэкс = ∑Mлев = 39,25∙4,97 – 8∙4,97∙0,5∙4,97 = 36,63 кН·м.
12. Производим статические проверки расчёта. Для этого из равновесия опорных узлов по построенным эпюрам MF и QF определяем опорные реакции (рис.13.21, г).
Для отсечённой от опор балки составляем уравнения равновесия
∑Y = 39,25 + 20,36 + 19,777 – 8∙8 – 15,333 = 79,333 – 79,333 = 0;
∑MA = – 62 – 20,306∙8 – 19,777∙14 + 15,333∙16 + 8∙8∙4 =
= – 501,326 + 501,328 ≈ 0.
Таким образом, проверки равновесия также выполняются. Следовательно, расчёт неразрезной балки произведён правильно.
Пример.13.2. Рассчитать раму (рис.13.22, а).
Решение.
Степень статической неопределимости при K =2, Ш = 4
nc = 3∙2 – 4 = 2.
2. Система канонических уравнений
δ11X1 + δ12X2 + Δ1F = 0;
δ21X1 + δ22X2 + Δ2F = 0.
3. Выбранная основная система показана на рис.13.22, б.
Основная система выбрана путём “врезки” двух шарниров в средний узел рамы. При этом реакция в удалённой угловой связи между стойкой и ригелем рамы X2 может быть отнесена как в левое, так и в правое от узла сечение ригеля.
4. Определяем усилия в основной системе от единичных моментов, последовательно прикладываемых по направлению удалённых связей (рис.13.22, в и г), Для этого определяем реакции от указанных воздействий и строим эпюры и .
5. Определяем усилия в основной системе от действия заданной нагрузки и строим эпюру (рис.13.22, д).
6. Определяем коэффициенты при неизвестных.
![]() (рад/кН·м).
(рад/кН·м).
![]() (рад/кН·м).
(рад/кН·м).
![]() (
рад/кН·м).
(
рад/кН·м).
7. Определяем свободные члены канонических уравнений.
![]() (рад);
(рад);
![]()
=![]() (рад).
(рад).
8. Производим решение системы канонических уравнений:

Упростим полученную систему уравнений, умножив все его члены на 0,5EI:
X1 – X2 + 103,5 = 0,
– X1 + 6X2 – 688,5 = 0.
Используя правило Г.Крамера, получим
![]() ;
;
![]() ;
;
![]() ,
,
откуда
![]()
9. Строим эпюру изгибающих моментов в заданной расчётной схеме
.
Все слагаемые приведённой формулы и результат сложения - эпюра MF показаны на рис.13.23, а.
10. Производим
деформационную проверку расчёта. Для
этого выбираем новую основную систему
(рис.13.23, б),
для которой строим эпюры
![]() ,
,
![]() и их сумму, эпюру
.
Сравнивая полученную эпюру
с эпюрами
и
,
использованными в расчёте, видим, что
она им не подобна, т.е. производимая
проверка будет достаточно корректна.
и их сумму, эпюру
.
Сравнивая полученную эпюру
с эпюрами
и
,
использованными в расчёте, видим, что
она им не подобна, т.е. производимая
проверка будет достаточно корректна.
![]()
![]()
![]() , т.е. проверка
выполнена.
, т.е. проверка
выполнена.
11. Производим построение эпюры QF на основании дифференциальной зависимости по участкам расчётной схемы.
Для этого разобьём схему рамы на участки, обозначив буквами их начало и конец (рис.13.24, а).
Участки A – K и K – D. Используя формулу (13.11), получаем
![]() ;
;
![]() .
.
Участок D – E. Используя формулу (13.12), получаем
.![]() ;
;
![]() .
.
Участки B – E и E – C. Используя формулу (13.11), получаем
![]() ;
;
![]() .
.
Построенная по полученным значениям эпюра QF показана на рис.13.24, б.
В левом пролёте эпюра QF имеет нулевое значение на расстоянии x0 от левой опоры. Вырезаем ригель рамы в левом пролёте рамы (рис.13.24, в) и находим экстремальное значение изгибающего момента в этом сечении.
Q0 = ∑Fлев = 26,5 – 8∙ x0 = 0, x0 = 3,31 м.
Mэкс = ∑Mлев = 26,5∙3,31– 8∙3,31∙0,5∙3,31 = 25,89 кН·м.
12. Определяем продольные силы в стержнях рамы и строим эпюру NF.
Для этого поочерёдно вырезаем узлы D и E рамы (рис.13.24, г) и из их равновесия находим продольные силы NAD , NDE и NBE. Построенная по полученным значениям эпюра показана на рис.13.24, д.
13. Производим статические проверки расчёта. Для этого из равновесия опорных узлов по построенным эпюрам NF и QF определяем опорные реакции (рис.13.24, е).
Для отсечённой от опор балки составляем уравнения равновесия
∑Y = 26,5 + 48 + 19,777 – 8∙9 – 2,5 = 74,5 – 74,5= 0;
∑X = 72 – 39 –33 – 8∙9 – 2,5 = 72 – 72= 0;
∑MA = 72∙3 + 8∙9∙4,5 – 48∙9 – 39∙3 + 2,5∙18 – 36 =
= – 585 + 585 = 0.
Таким образом, проверки равновесия также выполняются. Следовательно, расчёт неразрезной балки произведён правильно.
Пример.13.3. Построить эпюру изгибающих моментов в ригеле и определить продольные силы в стойке и подкосе комбинированной расчётной схемы (рис.13.25, а).
Решение.
1. Расчётная схема имеет число контуров K =3. Число простых шарниров (или связей, недостающих до полного защемления) определяем по узлам расчётной схемы.
Узел А: Ш =2. Узел В: Ш=2 (два примыкающих к основанию шарнира).
Узел C: Ш =3 (в опорной линейной связи не достаёт до полного защемления двух связей, и один шарнир соединяет стержни расчётной схемы). Узел D: Ш =1 (один примыкающий шарнир между двумя стержнями схемы). Итого Ш=8.
Степень статической неопределимости при K =3, Ш = 8
nc = 3∙3 – 8 = 1.
2. Каноническое уравнение
δ11X1 + Δ1F = 0.
3. Выбранная основная система показана на рис.13.25, б.
4. Определяем
усилия в основной системе от единичной
силы, приложенной по направлению
удалённой связи. Для этого определяем
реакции от указанного воздействия и
строим эпюры
и
![]() (рис.13.25,
в).
(рис.13.25,
в).
Так как в рассматриваемой расчётной схеме продольные усилия в ригеле отсутствуют, продольные силы в стойке и подкосе здесь и далее будем показывать (для упрощения графического материала) непосредственно на эпюрах изгибающих моментов.
5. Определяем усилия в основной системе от действия заданной нагрузки и строим эпюру (рис.13.25, г).
6. Определяем коэффициент при неизвестном канонического уравнения.
![]()
=![]() (м/кН).
(м/кН).
7. Определяем свободный член канонического уравнения.
![]()
=![]() (м/кН).
(м/кН).
8. Определяем неизвестное канонического уравнения:
X1 = – Δ1F/δ11 = – 468,741/44,393 = – 10,559 кН.
9. Строим эпюру изгибающих моментов в заданной расчётной схеме и определяем продольные силы в стойке и подкосе
![]() ;
;
![]() .
.
Результаты приведённых формул показаны на эпюре MF (рис.13.26, а).
Построение эпюры QF (рис.13.26, б) производится точно так же, как и в предыдущих примерах.
10. Для выполнения статических проверок расчёта определим реакции в опорных связях на основании принципа независимости действия сил.
RA = X1 = – 10,559 кН.
![]() = 320/3 + (4/3)∙(–
10,559) = 92,588 кН.
= 320/3 + (4/3)∙(–
10,559) = 92,588 кН.
![]() = 160 + (–1)∙(–
10,559) = 170,559 кН.
= 160 + (–1)∙(–
10,559) = 170,559 кН.
![]() =
320/3 + (4/3)∙(– 10,559) = 92,588 кН.
=
320/3 + (4/3)∙(– 10,559) = 92,588 кН.
Для отсечённой от опор комбинированной расчётной схемы составляем уравнения равновесия (рис. 13.26, в).
∑Y = 170,559 – 10,559 – 40∙4 = 0;
∑X = 92,588 – 92,588 = 0;
∑MB = 40∙4∙2 – 10,559∙4 – 92,588∙3 = 320 – 320 = 0.
Таким образом, проверки равновесия также выполняются. Следовательно, расчёт произведён правильно.
Пример 13.4. Определить усилия в консольной ферме (рис.13.27, а) при следующих соотношениях жёсткостей стержней: EA3C = EA; пояса – 2 EA; раскосы – 1,25 EA; стойки – EA.
Решение.
Степень статической неопределимости фермы при
У= 7, СФ = 9, Соп = 6 nc = С – 2У = (9 + 6) – 2∙7 = 1.
2. Каноническое уравнение
δ11X1 + Δ1F = 0.
3. Выбранная основная система показана на рис.13.27, б.
4. Определяем усилия в основной системе от единичной силы, приложенной по направлению удалённой связи, и строим эпюру (рис.13.27, в).
Определение усилий в ферме производим любым удобным способом – вырезания узлов или сечений.
5. Определяем усилия в основной системе от заданной нагрузки и строим эпюру (рис.13.27, г).
Дальнейший ход расчёта, включающий в себя определение коэффициента при неизвестном, свободного члена, решение канонического уравнения и определение усилий в заданной схеме фермы ( ), приведён в табл. 13.2.
Таблица 13.2
Определение усилий в статически неопределимой ферме
(к примеру 13.4)
№ стержня |
l, м |
|
|
, кН |
|
|
|
|
NF, кН |
1 – 2 2 – 3 3 – 4 4 – В 1 – 3 2 – 4 1 – 4 2 – В 3 - С |
4 4 4 4 3 3 5 5 10 |
2 2 2 2 1 1 1,25 1,25 1 |
0,8 1,6 -0,8 -1,6 0,6 0,6 -1 -1 1 |
-40 -120 0 40 0 -30 50 100 0 |
1,6 3,2 -1,6 -3,2 1,8 1,8 -4 -4 10 |
1,28 5,12 1,28 5,12 1,08 1,08 4 4 10 |
-64 -324 0 -128 0 -54 -200 -400 0 |
28,4 56,8 -28,4 -56,8 21,3 21,3 -35,5 -35,5 35,5 |
-11,6 -63,2 -28,4 -16,8 21,3 -8,7 14,5 64,5 35,5 |
EAδ11=∑= |
32,96 |
-1170 |
=∑= EAΔ1F |
||||||
X1= - EAΔ1F / EAδ11 = - (- 1170)/32,96 = 35,4976 ≈ 35,5 кН. |
|||||||||
13.4. Расчёт при наличии начальных деформаций
К начальным деформациям в расчётных схемах относят тепловое воздействие, неравномерную осадку опор и неточность изготовления стержней. Принципиально ход расчёта методом сил не меняется, так как основная система не зависит от вида воздействия. Влияние воздействий на расчётную схему учитывается только свободными членами системы канонических уравнений, которые в общем случае можно представить в виде
δ11X1 + δ12X2 + …+ δ1iXi +…+ δ1nXn +Δ1S = 0;
δ21X1 + δ22X2 + …+ δ2iXi +…+ δ2nXn +Δ2S = 0; , (13.13)
……………………………………………….
δn1X1 + δn2X2 + …+ δniXi +…+ δnnXn +ΔnS = 0.
где S – тип воздействия на расчётную схему (F, tº или Δ).
Свободные члены системы канонических уравнений, как перемещения в статически определимой основной системе, определяются:
–при расчёте на тепловое воздействие – по формуле (12.38);
–при расчёте на неравномерную осадку опор – по формуле (12.39);
–при расчёте на неточность изготовления стержней – по формуле (12.40).
Так как в статически определимых расчётных схемах, каковой является основная система, начальные деформации не вызывают никаких усилий, то формулы (13.8 -13.10) по определению усилий в заданных схемах принимают вид
для балок и рам
![]() ;
(13.14)
;
(13.14)
для ферм
![]() ;
(13.15)
;
(13.15)
для комбинированных систем
; .(13.16)
Основной особенностью поведения статически неопределимых расчётных схем при наличии начальных деформаций является прямая зависимость усилий от жёсткости элементов конструкции: чем больше жёсткость, тем значительнее усилия.
Пример 13.5. Построить эпюру изгибающих моментов Mt в раме при тепловом воздействии на стержень CD (рис.13.28, а). Рама изготовлена из гнутого замкнутого металлического профиля (ТУ 36 – 2287) 200 х 160 х 8,
Iz = 2147 см4. Коэффициент линейного расширения =120∙10-7 1/град. Высота сечения h = 0,2 м.
Решение.
1. Степень статической неопределимости при К =1 и Ш =2
nc = 3∙1 – 2 = 1.
2. Каноническое уравнение
δ11X1 + Δ1t = 0.
3. Выбранная основная система показана на рис.13.28, б.
4. Строим деформированную схему, определяем усилия в основной системе от единичной силы, приложенной по направлению удалённой связи, и строим эпюры и (рис.13.28, в).
5. Коэффициент при неизвестном
![]()
![]() (м/кН).
(м/кН).
6. Строим деформированную схему (состояние tº) основной системы от температурного воздействия (рис. 13.28, г).
7. Свободный член канонического уравнения по формуле (12.38):
Δ1t
=
αt{5∙(–1)∙5
+
![]() ∙3∙3}
= 2235 αt
(м).
∙3∙3}
= 2235 αt
(м).
8. Значение неизвестного X1 = – Δ1t /δ11 = –5,913 αt EI.
9. Эпюра изгибающих
моментов
![]() показана в двух вариантах: с общим
множителем αt
EI
(рис. 13.28, д)
и в действительных числах при αt
EI
= 120∙10-7∙2,06∙108∙2147∙10-8
= 53,07∙10-3
кН·м2/град
(рис 13.28, е).
показана в двух вариантах: с общим
множителем αt
EI
(рис. 13.28, д)
и в действительных числах при αt
EI
= 120∙10-7∙2,06∙108∙2147∙10-8
= 53,07∙10-3
кН·м2/град
(рис 13.28, е).
Пример 13.6. Построить эпюру изгибающих моментов MΔ в раме при осадке правой опоры на величину Δ = 0,27 м (рис.13.29, а). Рама изготовлена из двутавра № 24, Iz = 2900 см4.
Решение.
1. Степень статической неопределимости при К =1 и Ш =2
nc = 3∙1 – 2 = 1.
2. Каноническое уравнение
δ11X1 + Δ1Δ = 0.
3. Выбранная основная система показана на рис.13.29, б.
4. Строим деформированную схему, определяем усилия в основной системе от единичной силы, приложенной по направлению удалённой связи, и строим эпюру (рис.13.29, в).
5. Коэффициент при неизвестном
![]()
6. Строим деформированную схему основной системы (состояние ∆) от заданной осадки опор (рис. 13.29, г).
7. Свободный член канонического уравнения по формуле (12.39):
Δ1Δ
= – [![]() ]
= – 0,045 (м).
]
= – 0,045 (м).
8. Значение неизвестного X1 = – Δ1Δ /δ11 = 0,01EI.
9. Эпюра изгибающих
моментов
![]() показана в двух вариантах: с общим
множителем
EI
(рис. 13.29, д)
и в действительных числах при EI
= 2,06∙108∙2900∙10-8
= 5974 кН·м2
(рис. 13.29, е).
показана в двух вариантах: с общим
множителем
EI
(рис. 13.29, д)
и в действительных числах при EI
= 2,06∙108∙2900∙10-8
= 5974 кН·м2
(рис. 13.29, е).
Пример 13.7. Построить эпюру изгибающих моментов MΔ в раме при условии, что её затяжка изготовлена на величину Δ = 0,054 м короче, чем запроектирована (рис.13.30, а).
Рама изготовлена из двутавра № 16, Iz = 873 см4, а затяжка – из круглой стали d = 40 мм (A = 12,57 см2).
Жёсткость стержней рамы EI = 2,06∙108∙873∙10-8 = 1798,4 кН·м2.
Жёсткость затяжки EА = 2,06∙108∙12,57∙10-4 = 258 942 кН.
Соотношение жёсткостей EА/ EI = 258 942/1798,4 = 143,98 м-2.
Решение.
1. Степень статической неопределимости при К =2 и Ш =5
nc = 3∙2 – 5 = 1.
2. Каноническое уравнение
δ11X1 + Δ1Δ = 0.
3. Выбранная основная система показана на рис.13.30, б.
4. Строим деформированную схему, определяем усилия в основной системе от единичной силы, приложенной по направлению удалённой связи, и строим эпюру (рис.13.30, в).
5. Коэффициент при неизвестном
![]() .
.
6. Строим деформированную схему основной системы при заданном укорочении затяжки (состояние ∆). В результате того, что в качестве неизвестного метода сил выбрано усилие в затяжке, измененение ее длины в основной системе скажется только на самой затяжке (рис. 13.30, г).
7. Свободный член канонического уравнения по формуле (12.39):
Δ1Δ = 1∙(– 0,054)= – 0,054 (м).
8. Значение неизвестного X1 = – Δ1Δ /δ11 = 5,972∙10-3EI.
9. Эпюра изгибающих моментов показана в двух вариантах: с общим множителем EI (рис. 13.30, д) и в действительных числах при EI = 1798,4 кН·м2 (рис. 13.30, е).
13.5. Упрощения при расчёте симметричных систем
Использование естественных свойств симметрии может значительно упростить расчёт любой расчётной схемы как статически определимой . так и статически неопределимой. Особенно важно учитывать свойства симметрии при расчёте статически неопределимых систем, так как их учёт приводит к уменьшению числа разрешающих совместных уравнений. Поэтому, когда появляется возможность понизить число основных неизвестных, её следует реализовать.
Симметричной принято называть такую систему, геометрическая схема которой (влючая жёсткостные характеристики элементов) и расположение связей имеют одну или несколько общих осей симметрии.
Для всех сечений, расположенных на оси симметрии различают симметричные и кососимметричные статические (усилия) и кинематические (перемещения) факторы. Так, для сечения A горизонтально ориентированного стержня, расположенного на оси симметрии (рис.13.31), можно различить как:
cимметричные: изгибающий момент MA, продольная сила NA и вертикальное перемещение
 ;
;
кососимметричные: поперечная сила QA, угол поворота сечения φA и горизонтальное перемещение
 .
.
Нагрузка, действующая на симметричную расчётную схему, может также обладать свойствами симметрии. Она может быть как симметричной, так и кососимметричной. Кососимметричной называется нагрузка, которая относительно оси симметрии отличается лишь знаками.
Для реализации возможных упрощений при расчёте симметричных систем сформулируем их основные свойства.
Свойство 1. В симметричной расчётной схеме, загруженной симметрично расположенной нагрузкой (рис.13.32, а), деформационная схема (рис.13.32, б), эпюра изгибающих моментов (рис. 13.32, в) и эпюра продольных сил (рис.13.32, д) симметричны, а эпюра поперечных сил (рис.13.32, г) – кососимметрична.
Следствие 1. В симметричной расчётной схеме, загруженной симметричной нагрузкой в сечениях, расположенных на оси симметрии, кососимметричные статические и кинематические факторы равны нулю.
Например, для сечения А изображённой на рис. 13.32, а рамы, равны нулю QA, φA и .
Свойство 2. В симметричной расчётной схеме, загруженной кососимметрично расположенной нагрузкой (рис.13.33, а), деформационная схема (рис.13.33, б), эпюра изгибающих моментов (рис. 13.33, в) и эпюра продольных сил (рис.13.33, д) кососимметричны, а эпюра поперечных сил (рис.13.32, г) – симметрична.
Следствие 2. В симметричной расчётной схеме, загруженной кососимметричной нагрузкой в сечениях, расположенных на оси симметрии, симметричные статические и кинематические факторы равны нулю.
Например, для сечения А изображённой на рис. 13.33, а рамы, равны нулю MA, NA и .
При действии на расчётную схему симметричной или кососимметричной нагрузок, используя свойства 1 и 2 и следствия к ним, можно рассматривать не всю расчётную схему, а лишь её симметричную часть.
Так для симметричной рамы, загруженной симметричной нагрузкой (рис. 13.34, а) и имеющую степень статической неопределимости nc =3, статические и кинематические условия для сечения А на оси симметрии будут следующими:
QA = 0, MA ≠ 0, NA ≠ 0; 2. φA =0, = 0, ≠ 0.
Для того, чтобы симметричная часть расчётной схемы удовлетворяла этим условиям, необходимо на оси симметрии поставить подвижное в вертикальном направлении защемление. Степень статической неопределимости полученной схемы nc =2. Налицо сокращение числа канонических уравнений.
По аналогии, для симметричной рамы, загруженной кососимметричной нагрузкой (рис. 13.34, б) и имеющую степень статической неопределимости nc =3, статические и кинематические условия для сечения А на оси симметрии будут следующими:
QA ≠ 0, MA = 0, NA = 0; 2. φA ≠ 0, ≠ 0, = 0.
Для того, чтобы симметричная часть расчётной схемы удовлетворяла этим условиям, необходимо на оси симметрии поставить шарнирно подвижную опору, разрешающую горизонтальные смещения сечения А. Степень статической неопределимости полученной схемы nc =1. В этом случае так же имеем сокращение числа канонических уравнений.
На основании вышеприведённых свойств симметричных расчётных схем используют два приёма упрощения расчётов симметричных систем: способ разложения нагрузки и способ группировки неизвестных.
Применение этих способов возможно лишь в случае использования симметричных основных систем метода сил.
Рассмотрим оба этих способа.
С п о с о б р а з л о ж е н и я н а г р у з к и
Любую произвольную нагрузку, действующую на симметричную расчётную схему, на основании принципа независимости действия сил всегда можно разложить на симметричную и кососимметричную (рис.13.35, а). Разложение должно удовлетворять условию – сумма симметричного и кососимметричного загружений должна быть равна заданному загружению.
Расчёт от каждого вида загружения производится отдельно. Затем на основании принципа независимости действия сил результаты складываются. Например, для расчётной схемы, работающей в условиях изгиба
![]() .
.
Рассмотрим подробнее, какие упрощения мы можем получить при использовании способа разложения нагрузки, на примере трижды статической неопределимой рамы (рис.13.35).
Выберем симметричную основную систему метода сил, симметрично удалив избыточные связи путём ”врезки” шарниров в опорные защемления и в середину ригеля рамы (рис.13.35, б) и обозначив реакции в удалённых связях как Y1,Y2 и Y3.
При действии симметричной нагрузки (рис.13.35, б) на основании свойства 1 получим, что Y3 = –Y1= X1, а неизвестное Y2 обозначим через X2. В результате получили два неизвестных и, следовательно, систему канонических уравнений второго порядка. При этом групповое неизвестное X1 и неизвестное X2 являются симметричными.
При действии кососимметричной нагрузки (рис.13.35, в) на основании свойства 2 получим, что Y3 = Y1= X3, а неизвестное Y2 = 0. В результате получили одно неизвестное и, следовательно, одно каноническое уравнение. При этом групповое неизвестное X3 является кососимметричным.
В итоге для рассматриваемой рамы вместо системы уравнений с тремя неизвестными мы имеем независимые друг от друга систему уравнений с двумя неизвестными и одно уравнение с одним неизвестным. В этом и состоит упрощение расчёта. Сумма неизвестных при обоих вида загружения равна степени статической неопределимости рамы, т.е. nс + nкс = nc.
Преимущество данного способа состоит в том, что он позволяет рассматривать при каждом виде загружения не всю расчётную схему, а лишь её симметричную часть, как это было показано на рис.13.34. Перед суммированием результатов на отброшенной при расчёте симметричной части эпюры усилий достраиваются из условий симметрии, сформулированных в свойствах 1 и 2.
Способ разложения, естественно, может быть применён не только при действии внешней нагрузки, но и при любых воздействиях на расчётную схему. На рис. 13.36 показаны примеры разложения на симметричное и кососимметричное теплового воздействия и неравномерной осадки опор.
С п о с о б г р у п п и р о в к и н и з в е с т н ы х
Рассмотрим симметричную дважды статически неопределимую раму (рис.13.37, а), для которой выберем симметричную основную систему, удалив левую и правую шарнирно подвижные опоры. Неизвестные реакции в удалённых связях Y1и Y2 представим в виде (рис.13.37, б)
Y1 = X1 + X2 и Y2 = X1 – X2.
В полученном представлении X1 – групповое симметричное неизвестное, а X2 – групповое кососимметричное неизвестное.
Канонические уравнения для указанных групповых неизвестных имеют вид
δ11X1 + δ12X2 + Δ1F = 0;
δ21X1 + δ22X2 + Δ2F = 0.
В силу свойств симметрии в состояниях 1 и 2 (рис.13.37, в и г) получим симметричную эпюру и кососимметричную эпюру . Перемножение этих эпюр даёт
![]() ,
,
т.е. результат “перемножения” симметричной эпюры усилий на кососимметричную равен нулю.
Следовательно, выше приведённая система уравнений принимает вид
δ11X1 + Δ1F = 0;
δ22X2 + Δ2F = 0.
Таким образом, при использовании способа группировки неизвестных система канонических уравнений, записанная для групповых неизвестных, распадается на две группы: для симметричных и кососимметричных неизвестных из-за равенства нулю побочных коэффициентов канонических уравнений. В этом и состоит эффект использования симметрии.
При этом эпюра грузового состояния (рис.13.37, д) строится от заданной нагрузки и может быть любой. Эпюра изгибающих моментов в заданной расчётной схеме строится на основании принципа независимости действия сил по формуле (13.14).
Приведённый на примере достаточно простой расчётной схемы вывод справедлив при любой степени статической неопределимости и для любого типа расчётных схем.
Подобный эффект “обнуления” побочных коэффициентов может быть получен при удалении избыточных связей непосредственно на оси симметрии расч1ётной схемы. Так, для той же рамы (рис.13.38, а) основная система (рис.13.38, б) получена удалением связей центрального шарнира ригеля. В результате при рассмотрении вспомогательных состояний (рис.13.38, в и г) получим симметричную эпюру и кососимметричную эпюру и, как следствие, δ12 = δ21=0. Усилия грузового состояния основной системы определяются от заданного воздействия (рис. 13.38, д).
Оба рассмотренных приёма использования симметрии при расчёте статически неопределимых систем равнозначны. Второй не требует разложения внешнего воздействия, а первый позволяет рассматривать симметричную часть расчётной схемы, что уменьшает количество исходных данных при решении задачи на ЭВМ.
Рассмотрим несколько примеров использования симметрии при решении статически неопределимых задач.
Пример. 13.8.
Построить эпюру изгибающих моментов
![]() для трёхпролётной симметричной балки
(рис.13.39, а),
загруженной симметричной нагрузкой.
для трёхпролётной симметричной балки
(рис.13.39, а),
загруженной симметричной нагрузкой.
Решение.
Степень статической неопределимости при К = 3, Ш = 8
nc = 3∙3 – 8 = 1.
Каноническое уравнение δ11X1 + Δ1F = 0.
Основную систему (рис.13.39, б) получим, удалив вертикальную связь в шарнире С, расположенном на оси симметрии.
На основании следствия 1 неизвестное X1 = 0 как кососимметричный статический фактор.
Поэтому заданная схема балки рассчитывается как статически определимая (рис.13.39, в). Эпюра изгибающих моментов для неё представлена на рис.13.39, г.
Пример.13.9. Построить эпюру изгибающих моментов для рамы с затяжкой (рис.13.40, а), загруженной кососимметричной нагрузкой.
Решение.
Степень статической неопределимости при К = 2, Ш = 4
nc = 3∙2 – 4 = 2.
Система канонических уравнений
δ11X1 + δ12X2 + Δ1F = 0;
δ21X1 + δ22X2 + Δ2F = 0.
Основную систему (рис.13.40, б) получим, врезав шарнир в середине ригеля рамы и удалив затяжку.
На основании следствия 2 неизвестные X1 = X2 = 0 как симметричные статические факторы.
Поэтому заданная схема балки рассчитывается как статически определимая (рис.13.40, в). Эпюра изгибающих моментов для неё представлена на рис.13.40, г.
Пример.13.10. Построить эпюру изгибающих моментов для симметричной балки с осью ломаного очертания (рис.13.41, а).
Решение.
Степень статической неопределимости при К = 3, Ш = 7
nc = 3∙3 – 7 = 2.
Система канонических уравнений
δ11X1 + δ12X2 + Δ1F = 0;
δ21X1 + δ22X2 + Δ2F = 0.
Основную систему (рис.13.41, б) получим, удалив связи в опорах A и B. Для неизвестных реакций в удалённых связях применим способ группировки.
4. Определяем усилия в основной системе от единичных сил, последовательно прикладываемых по направлению удалённых связей (рис.13.41, в и г). Для этого определяем реакции от указанных воздействий и строим эпюры и .
5. Определяем усилия в основной системе от действия заданной нагрузки и строим эпюру (рис.13.41, д).
6. Определяем коэффициенты при неизвестных.
![]() (м/кН);
(м/кН);
δ12 = δ21 = 0;
![]() (м/кН).
(м/кН).
7. Определяем свободные члены канонических уравнений.
![]() (м);
(м);
![]() (м).
(м).
8. Производим решение системы канонических уравнений:
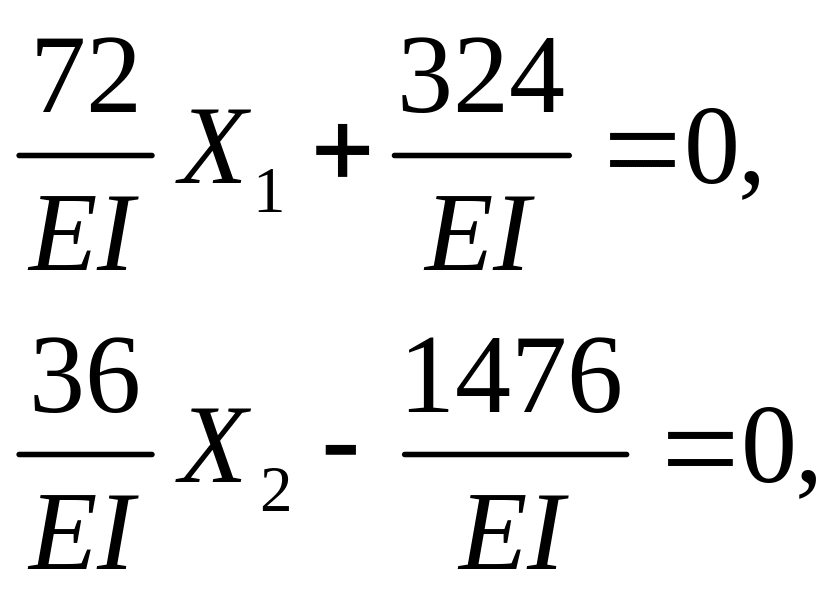
откуда X1 = – Δ1F / δ11= – 324/72 = – 4,5 кН,
X2 = – Δ2F / δ22= – (–1476/360) = 4,1 кН.
9. Строим эпюру изгибающих моментов в заданной расчётной схеме
.
Все слагаемые приведённой формулы и результат сложения - эпюра MF показаны на рис.13.42.
Последующий ход расчёта см. пример 13.2.
Пример.13.11. Построить эпюру изгибающих моментов для симметричной рамы (рис.13.43, а).
Решение.
Степень статической неопределимости при К = 2, Ш = 4
nc = 3∙2 – 4 = 2.
Система канонических уравнений
δ11X1 + δ12X2 + Δ1F = 0;
δ21X1 + δ22X2 + Δ2F = 0.
Основную систему (рис.13.43, б) получим, удалив связи в шарнире С. Поскольку избыточные связи удалены на оси симметрии, группировки неизвестных не требуется.
4. Определяем усилия в основной системе от единичных сил, последовательно прикладываемых по направлению удалённых связей (рис.13.43, в и г). Для этого определяем реакции от указанных воздействий и строим эпюры и .
5. Определяем усилия в основной системе от действия заданной нагрузки и строим эпюру (рис.13.49, д).
6. Определяем коэффициенты при неизвестных.
![]() (м/кН);
(м/кН);
δ12 = δ21 = 0;
![]() (м/кН).
(м/кН).
7. Определяем свободные члены канонических уравнений.
![]() (м);
(м);
![]() (м).
(м).
8. Производим решение системы канонических уравнений:

откуда X1 = – Δ1F / δ11= – 5832/360 = – 16,2 кН,
X2 = – Δ2F / δ22= – 1944/144 = – 13,5 кН.
9. Строим эпюру изгибающих моментов в заданной расчётной схеме
.
Все слагаемые приведённой формулы и результат сложения - эпюра MF показаны на рис.13.43, е – з.
Последующий ход расчёта см. пример 13.2.
13.6. Понятие о расчёте пространственных рам
Пространственные рамы – стержневые системы, элементы которых работают в условия сложного напряжённого состояния. Они, как правило, многократно статически неопределимы.
Методы расчёта пространственных рам те же, что и для плоских статически неопределимых рам. В то же время расчёт пространственных рам значительно сложнее как за счёт значительно бóльшей статической неопределимости, так и большим числом силовых факторов, действующих в элементах таких расчётных схем.
В ряде случаев при расчёте пространственную раму заменяют несколькими плоскими рамами. Это осуществимо, если основные несущие элементы и действующие нагрузки находятся в параллельных плоскостях.
Для пространственных систем, как и для плоских справедлива зависимость (13.1). Тогда на основании (1.7) степень статической неопределимости пространственной системы может быть определена по формуле
nc = (Соп + 6Ж + С) – 6Т . (13.17)
Для бесшарнирных пространственных рам с защемлёнными опорами степень их статической неопределимости удобнее определять по количеству разрезов nр, которые необходимо произвести, чтобы превратить пространственную раму в набор статически определимых пространственных консолей:
nc = 6 nр. (13.18)
Основная система метода сил при расчёте пространственных рам выбирается так же, как и для плоских, т.е. путём удаления избыточных связей в элементах, узлах или на опорах расчётной схемы. При этом могут быть использованы все использованные ранее приёмы выбора рациональной основной системы, приводящие к обращению в нуль как можно большее число побочных коэффициентов при неизвестных системы канонических уравнений.
Как и при расчёте плоских рам в пространственных рамах при определении перемещений пренебрегают влияние продольных и поперечных сил, т.е. используют формулу (12.26). Выражения для определения коэффициентов при неизвестных и свободных членов на основании указанной формулы будут следующими:
 ;
(13.19)
;
(13.19)
 .
(13.20)
.
(13.20)
Здесь My, Mz – изгибающие, а Mx = Mк – крутящий моменты, отнесённые к местной системе координат поперечного сечения (см. рис.4.6)
Определение усилий в заданной расчётной схеме и построение эпюр MxF, MyF, MzF осуществляется на основании принципа независимости действия сил по аналогии с формулой (13.8):
![]() ;
;
![]() (13.21)
(13.21)
![]() .
.
Поперечные силы, как и при расчёте плоских рам, находятся на основании дифференциальных зависимостей:
![]() ;
;
![]() .
(13.22)
.
(13.22)
Продольные силы в стержнях пространственных рам находятся из условия равновесия узлов по найденным значениям поперечных сил. Узлы следует вырезать в такой последовательности, чтобы в каждом было не более трёх неизвестных продольных сил в сходящихся в рассматриваемом узле стержнях.
Основными проверками расчёта являются деформационная и статические.
Все выше перечисленные эпюры в процессе расчёта могут строиться как по отдельности, так и объединятся в один чертёж (если позволяет его наглядность) по типу рассматриваемого состояния.
Пример.13.12. Построить эпюры изгибающих моментов и поперечных сил для рамы (рис.13.44, а) при следующих данных: GIк = EIz = EIy = EI.
Решение.
1. Для представления расчётной схемы в виде пространственных статически определимых консолей достаточно одного разреза, например, разрезая ригель рамы посередине.
Следовательно, степень статической неопределимости на основании (13.18) будет nc = 6∙1= 6.
Поэтому основную систему выбираем, разрезая ригель по вертикальной плоскости симметрии схемы. В проведённом разрезе в общем случае действуют шесть внутренних сил.
Так как действующая нагрузка перпендикулярна плоскости рамы то в проведённом сечении Nx = 0, Qz= 0 и My = 0. В силу симметрии заданной схемы относительно вертикальной плоскости в сечении, принадлежащем этой плоскости должны равняться при симметричной нагрузке кососимметричные статические факторы, т.е. Qy = 0 и Mx = 0. Таким образом, из всех возможных усилий в рассматриваемом сечении остаётся только изгибающий момент Mz= X1 (рис.13.44, б).
2. Каноническое уравнение
δ11X1 + Δ1F = 0.
3. Определяем усилия в основной системе от единичного момента, приложенной по направлению удалённой связи и строим эпюру (рис.13.44, в), объединяя в ней изгибающие моменты в вертикальной плоскости и крутящие моменты.
4. Определяем усилия в основной системе от действия заданной нагрузки и строим эпюру (рис.13.44, д), также как и в предыдущем случае объединяя на одном чертеже изгибающие и крутящие моменты.
5. Определяем коэффициент при неизвестном канонического уравнения.
![]() (рад/кН·м).
(рад/кН·м).
6. Определяем свободный член канонического уравнения.
![]() (рад).
(рад).
7. Определяем неизвестное канонического уравнения:
X1 = – Δ1F/δ11 = – 373,33/12 = – 31,11 кН·м.
8. Строим эпюру изгибающих моментов в заданной расчётной схеме.
.
9. На основании дифференциальных зависимостей определяем поперечные силы в стержнях рамы и строим эпюру QF.
Эпюры QF и MF показаны на рис.13.44, д и е.
Контрольные вопросы
Какие расчетные схемы называются статически неопределимыми?
Что называется степенью статической неопределимости?
Как может быть определена степень статической неопределимости плоских расчетных схем?
Сформулируйте основные свойства статически неопределимых систем.
Какая расчетная схема называется основной системой метода сил?
Какие требования предъявляются к основной системе метода сил?
Как получить из заданной статически неопределимой расчетной схемы основную систему метода сил?
Сформулируйте смысл канонических уравнений метода сил.
Какой принцип строительной механики положен в основу определения усилий в статически неопределимой расчетной схеме?
Каков порядок расчета методом сил при действии внешней нагрузки для балок и рам, комбинированных расчетных схем, ферм?
Как зависят усилия в стержнях статически неопределимой расчетной схемы от их жесткости?
Какие Вы знаете проверки расчета статически неопределимых систем методом сил?
Как в канонических уравнениях метода сил учитывается влияние начальных деформаций?
От каких параметров зависят усилия в статически неопределимой расчетной схеме при наличии начальных деформаций?
Какие расчетные схемы называются симметричными?
Сформулируйте основные свойства симметричных расчетных схем.
Какие статические и кинематические факторы на оси симметрии расчетной схемы относятся к симметричным, а какие – к кососимметричным?
Какие способы упрощения расчета симметричных расчетных схем Вы знаете? Дайте их характеристики.
Как определяется степень статической неопределимости пространственных рам?
В чем состоят особенности расчета пространственных рам методом сил?
Глава 14 расчёт статически неопределимых систем методом перемещений
14.1. Основные положения. Степень кинематической неопределимости
Метод перемещений является вторым основным классическим методом расчёта статически неопределимых систем. Основными неизвестными в этом методе являются угловые и линейные смещения узлов расчётной схемы (рис. 14.1), что и определило его название. Во многих случаях метод перемещений является эффективнее метода сил.
Рассмотрим деформированное состояние статически неопределимой рамы (рис. 14.1) при действии внешней нагрузки.
Для упрощения расчёта используются общепринятые и ранее сформулированные допущения о пренебрежении продольными деформациями в изгибаемых стержнях и о малости деформаций по сравнению с размерами сооружения. В силу этих допущений жёсткие узлы рассматриваемой рамы остаются прямыми, горизонтальные смещения узлов C и D считаются одинаковыми, углы поворота жёстких узлов в силу их малости определяются по тангенсу угла, пренебрегается сближением концов стержней при их и изгибе (например, узлы С и D по вертикали не перемещаются).
Для того, чтобы применить метод перемещений, необходимо знать степень упругой подвижности узлов расчётной схемы (степень кинематической неопределимости), включающую количество независимых угловых и линейных перемещений всех узлов:
nк = nу + nл, (14.1)
где nу – число жёстких узлов расчётной схемы, способных к повороту при её деформации; nл – степень линейной подвижности всех узлов схемы.
Применение формулы (14.1) покажем на примере рамы, изображённой на рис. 14.2, а. Рама имеет как полностью жёсткие узлы, так и комбинированные. В число nу включаются лишь жёсткие соединения стержней. Кроме этого узлами считаются места ступенчатого изменения жёсткостных характеристик (узел А). Ригель ВС в представленной схеме показан абсолютно жёстким, т.е. не изгибаемым, поэтому узлы В и С не способны к повороту. Все жёсткие узлы, способные к повороту при деформации рассматриваемой рамы отмечены пунктиром на рис. 14.2, б. Таким образом, для данной рамы nу = 6.
Степень линейной подвижности может быть определена как степень свободы шарнирного механизма, полученного из заданной схемы рамы путём введения сквозных шарниров во все её узлы, включая опорные:
nл =W = 2У – (Сф + Соп). (14.2)
Для рассматриваемой рамы (рис.14.2, в): У = 13, Сф = 14, Соп = 8, поэтому
nл = 2∙13 – (14 + 8) = 4, и степень кинематической неопределимости nк = nу + nл = 6 + 4 = 10.
В случае простых схем (рис.14.1) число линейных смещений узлов определяется непосредственно из анализа возможной схемы деформированного состояния, и использование формулы (14.2) не обязательно.
В отличие от метода сил, рассмотренного в предыдущей главе, основная система метода перемещений получается не удалением, а введением дополнительных связей. Дополнительные связи вводятся по направлению возможных смещений узлов расчётной схемы как угловых, так и линейных. В результате все узлы расчётной схемы становятся неподвижными.
Основная система, получаемая введением дополнительных связей по направлению возможных смещений узлов, называется кинематически определимой.
В качестве вводимых дополнительных связей применяются жёсткие линейные связи, устраняющие линейные перемещения узлов, и “плавающие” заделки, устраняющие повороты узлов. Термин “плавающая” заделка применяется в том смысле, что она может иметь линейные смещения, т.е. свободно перемещаться вместе с узлом, но не может поворачиваться до тех пор, пока ей не будет сообщён принудительный поворот. В соответствии с изложенным в качестве неизвестных принимаются линейные смещения и углы поворота по направлению введённых дополнительных связей.
Для рамы, приведённой на рис. 14.2, а, основная система показана на рис. 14.2, г.
В отличие от основной системы метода сил кинематически определимая основная система единственна. Различие может состоять лишь в месте установки какой-либо линейной связи. Например, дополнительная горизонтальная связь 8 (рис. 14.2, г) может быть установлена в любом из узлов первого этажа рамы.
В результате введения дополнительных связей расчётная схема превращается в набор отдельных прямолинейных стержней постоянного сечения двух типов (рис. 14.3). Указанные стержни являются простыми статически неопределимыми однопролётными балками, которые могут быть рассчитаны от любого воздействия методом сил. Результаты таких расчётов в общем виде обычно сводятся в специальные таблицы, называемые таблицами реакций (прил. 10 и 11). В таблицах приложения 10 все значения реакций выражены через величину i =EI/l (отношение жёсткости стержня при изгибе к его длине), называемой относительной жёсткостью стержня.
14.2. Идея метода перемещений. Система канонических уравнений и общая последовательность расчёта
Для описания идеи метода рассмотрим простейшую расчётную схему – двухпролётную одноэтажную несвободную раму, т.е. раму, не имеющую линейных смещений узлов (рис. 14.4, а). Рама загружена произвольной нагрузкой и является дважды кинематически неопределимой.
Предположим, что узлы A и B при деформации рамы под нагрузкой будут поворачиваться на какие-то углы Z1 и Z2.
Введём дополнительные угловые связи в узлы A и B (рис. 14.4, б). Полученная схема является кинематически определимой и называется основной системой метода перемещений.
Для полученной основной системы воспользуемся принципом независимости действия сил и рассмотрим следующие воздействия: состояние 1 от принудительного поворота первой связи на угол Z1 (рис. 14.4, в); состояние 2 от принудительного поворота второй связи на угол Z2 (рис. 14.4, г) и состояние F от действия внешней нагрузки (рис. 14.4, д).
Во всех перечисленных состояниях в связях, введённых в узлы А и B, появятся реакции, которые будем считать положительными, если их направление совпадает с направление принудительного смещения связи. Сумма реакций по каждому из указанных направлений даст полные реакции во введённых дополнительных связях
RA =R11 + R12 + R1F;
RB =R21 + R22 + R2F .
Чтобы основная система соответствовала по своим статическим свойствам заданной расчётной схеме, очевидно, необходимо выполнения условий
RA = 0; RB = 0
и
(14.3)
R21 + R22 + R2F = 0 .
Для выражения перемещений, входящих в (14.3) воспользуемся зависимостью (12.20) и запишем
R11 = r11Z1; R12 = r12Z2; R21 = r21Z1; R22 = r22Z2.
П одставив эти выражения в (14.3), получим
(14.4)
r21Z1 + r22Z2 + R2F = 0.
Запись (14.4) называется системой канонических уравнений метода перемещений.
Как и (14.3), система канонических уравнений метода перемещений имеет следующий статический смысл: сумма реакций в дополнительных связей от смещения этих связей и внешнего воздействия равна нулю.
Приведённый вывод системы канонических уравнений справедлив для любой расчётной схемы с любой степенью кинематической неопределимости. Поэтому, если степень кинематической неопределимости nк = n, то система канонических уравнений будет иметь вид:
r11Z1 + r12Z2 + …+ r1iZi +…+ r1nZn +R1F = 0;
r21Z1 + r22Z2 + …+ r2iZi +…+ r2nZn +R2F = 0; (14.5)
……………………………………………….
rn1Z1 + rn2Z2 + …+ rniZi +…+ rnnZn +RnF = 0.
В системе канонических уравнений (14.5) коэффициенты при неизвестных с одинаковыми индексами называются главными коэффициентами и они всегда положительны rii > 0. Остальные коэффициенты называются побочными, и для них выполняется теорема о взаимности возможных реакций rik = rki.
Размерности коэффициентов при неизвестных и свободных членов системы канонических уравнений легко определяются на основании их статического смысла, сформулированного выше.
Так, для рамы, использованной при выводе системы канонических уравнений (рис. 14.4, а), неизвестными метода перемещений являются углы поворота (единицы измерения – рад), реакциями в угловых связях (защемлениях) по направлению углов будут пары сил (единицы измерения – кН·м). Следовательно, свободные члены системы уравнений, являющиеся реакциями от действующей нагрузки, будут измеряться в кН·м, а все коэффициенты при неизвестных – в кН·м / рад.
Если основная система метода перемещений получена введение как угловых, так и линейных дополнительных связей (рис. 14.5), то, рассуждая аналогично, получим нижеследующее.
В направлении первого неизвестного отрицается сумма реакций в угловой связи, которые имеют единицы измерения в кН·м. Так как Z1 измеряется в рад, а Z2 – в м, то единицами измерения коэффициентов при неизвестных первого уравнения будут: для r11 – кН·м/ рад, для r12 – кН, а для свободного члена R1F – кН·м.
Аналогично, второе уравнение отрицает в направлении второго неизвестного сумму линейных реакций, измеряемых в кН. Значит, для второго уравнения единицами измерения коэффициентов при неизвестных будут: для r21 – кН / рад, для r22 – кН /м, а для R2F – кН.
Коэффициенты при неизвестных и свободные члены системы канонических уравнений метода перемещений при расчёте ортогональных рам определяются :
реакции в угловых связях – из условия равновесия узла, в который введена дополнительная связь;
реакции в линейных связях – способом сечений, которые проводятся параллельно оси связи через все стержни схемы, которые деформируются при принудительном смещении этой связи.
Последовательность расчёта методом перемещений
Определение степени кинематической неопределимости расчётной схемы nк = nу + nл.
Составление системы канонических уравнений в общем виде.
Получение основной системы метода перемещений путём введения дополнительных связей по направлению возможных смещений узлов расчётной схемы.
Получение деформированных схем и определение усилий в основной системе (построение эпюр ) от последовательного принудительного смещения дополнительных связей (i = 1…n = nк) по прил.10.
Определение усилий в основной системе (построение эпюры ) по прил.11.
Определение коэффициентов при неизвестных rik и свободных членов RiF системы канонических уравнений.
Запись системы канонических уравнений метода перемещений в численном виде и определение неизвестных Zi из её решения.
Определение усилий в заданной расчётной схеме на основании принципа независимости действия сил
![]() .
(14.6)
.
(14.6)
Первая статическая проверка расчёта.
Целью её является проверка равновесия жёстких узлов расчётной схемы по значениям изгибающих моментов, полученных по эпюре MF (14.6). При правильном расчёте для каждого жёсткого узла должно выполняться условие ∑Mузл = 0.
10. Деформационная проверка расчёта. Для её проведения выбирается любая основная статически определимая система, в которой от последовательного приложения единичных сил строятся эпюры (при i = 1…n=nc) и их сумма . При правильном расчёте должны выполняться условия
либо .
11. Построение эпюры поперечных сил QF на основании дифференциальной зависимости с использованием формул (13.11) и (13.12).
12. Определение продольных сил в стержнях расчётной схемы из условия равновесия её узлов и построение эпюры NF.
13. Статически проверки расчёта. При правильном расчёте любая отсеченная часть расчётной схемы или вся схема, отсечённая от опор, под действием внутренних и внешних сил должна находиться в равновесии.
Как видно из выше приведённого п.п. 10 – 13 настоящей последовательности ничем не отличаются от п.п. 11 – 14 табл. 13.11 при расчёте методом сил, т.е. в независимости от метода расчёта указанные пункты выполняются одинаково.
Рассмотрим несколько примеров расчёта рам методом перемещений.
Пример 14.1. Построить эпюры усилий в раме (рис. 14.6, а).
Относительные жёсткости стержней рамы, приведённые к единому множителю:
правая стойка i1 = EI/4 = i;
левая стойка i2 = 1,5EI/4 = 1,5i;
ригель i3 = 2EI/4 = 2i.
Решение.
1. Рама имеет один жёсткий узел, и два её узла могут совместно перемещаться по горизонтали. Следовательно, степень кинематической неопределимости рамы nк = 2.
2. Система канонических уравнений на основании (14.5) при nк = 2 будет иметь вид r11Z1 + r12Z2 + R1F = 0;
r21Z1 + r22Z2 + R2F = 0.
3. Основная система, полученная введением одной угловой и одной линейной дополнительных связей, показана на рис. 14. 6, б.
4. Последовательно задаём введенным дополнительным связям принудительные единичные смещения, показываем деформированные схемы основной системы от этих смещений (рис. 14.6, в и г) и по таблицам прил. 10 строим в основной системе эпюры и .
5. Прикладывая к стержням основной системы и на основании таблицы прил.11строим эпюру (рис. 14.6, д).
6. Определение реакций в дополнительных связях определяем в следующей последовательности.
Сначала определим реакции первого канонического уравнения, описывающего статическое условие равенства нулю суммы реакций в угловой дополнительной связи. Для этого вырезаем узел вместе со связью (рис. 14.7, а), последовательно прикладывая к нему изгибающие моменты с эпюр , и , соответствующих трём расчётным состояниям. Из условия равновесия получаем:
r11 = 9i (кН·м/рад), r12 = – 9i/4 (кН), R1F = –72 (кН·м).
Для определения реакций второго канонического уравнения, описывающего статическое условие равенства нулю суммы реакций в линейной связи, для каждого из расчётных состояний рассматриваем отсечённую часть основной системы (сечения I – I, II – II и F – F, рис. 14.7, б) и из условия их равновесия определяем:
r21 = – 9i/4 (кН/рад), r22 = 21i/16 (кН/м), R2F = 15 (кН).
7. Система канонических уравнений в численном виде будет иметь вид:

а его решение Z1 = 9/i (рад), Z2 = 4/i (м).
8. Строим эпюру
изгибающих моментов в заданной схеме
на основании (14.6)
![]() .
.
Все указанные слагаемые приведены на рис.14.8, а, а результат сложения – на рис. 14.8, б.
9. Проверка равновесия жёсткого узла по полученной эпюре в данной задаче может быть сделана визуально, так как в узле сходится всего два стержня.
10. Для проведения деформационной проверки определяем степень статической неопределимости рамы. При К =1, Ш =1 nc = 3∙1 – 1 = 2. основная статически определимая основная система для рамы показана на рис. 14.9, а. В приведённой основной системе построена вспомогательная эпюра от действия сразу двух единичных моментов, приложенных по направлениям удалённых связей. Тогда
![]()
следовательно, деформационная проверка выполняется.
11. Эпюры QF и NF, построенные по ранее приведённой методике (см. пример 13.2, п.п. 11 и 12) приведены на рис. 14.8, б.
12. Производим статические проверки расчёта, рассматривая равновесие всей рамы, предварительно определив по построенным эпюрам все опорные реакции (рис. 14.9, б).
∑X = 0, 15,75 + 32,25 – 48 = 0;
∑Y = 0, 41,625 + 30,375 – 9∙8 = 0;
∑MA = 0, 18 + 9∙8∙4 – 48∙2 + 33 – 30,375∙8 = 339 – 339 = 0.
Таким образом, статические проверки также выполняются, следовательно, расчёт произведён правильно.
Пример 14.2. Построить эпюру изгибающих моментов MF в раме (рис. 14.10, а).
Относительные жёсткости стержней рамы одинаковы, так как 1,25EI/5 = = EI/4 = i.
Решение.
1. Степень кинематической неопределимости рамы в силу линейной неподвижности её узлов nк = nу = 1.
2. Следовательно, каноническое уравнение метода перемещений будет единственным r11Z1 + R1F = 0.
3. Основная система, полученная введением одной дополнительной угловой связи, показана на рис. 14.10, б.
4. Деформированная схема основной системы от принудительного поворота дополнительной связи на угол, равный единице, и соответствующая ей эпюра , построенная по таблицам прил.10, показаны на рис. 14.10, в.
5. В силу того, что стержни основной системы не загружены, так как внешняя действующая нагрузка является узловой и непосредственно воспринимается введённой дополнительной угловой связью, то в грузовом состоянии эпюра = 0.
6. Реакции в дополнительной связи в обоих расчётных состояниях, определённые из условий равновесия дополнительной связи (рис. 14.10, г) равны: r11 = 7i (кН·м/рад), R1F = 56 (кН·м).
7. Каноническое уравнение в численном виде
7iZ1 + 56 = 0,
откуда Z1 = – 56/7i = – 8/i (рад).
Эпюра изгибающих моментов в заданной схеме рамы будет получена как
 ,
т.к.
= 0 (рис. 14.10, д).
,
т.к.
= 0 (рис. 14.10, д).
Пример 14.3. Построить эпюру изгибающих моментов MF в раме (рис.14. 11, а).
Относительные жёсткости стержней рамы:
левая стойка i1 = EI/4 = i;
правые стойки i2 = 2EI/4 = 2i.
Ригель рамы имеет бесконечную жёсткость при изгибе, поэтому узлы рамы неспособны к повороту.
Решение.
1. Степень кинематической неопределимости рамы nк = nс = 1. т.к. узлы рамы поворачиваться не могут, а для ригеля за счёт изгиба стоек рамы возможно одно горизонтальное линейное смещение.
2. Следовательно, каноническое уравнение метода перемещений будет единственным r11Z1 + R1F = 0.
3. Основная система, полученная введением одной дополнительной линейной связи, показана на рис. 14.11, б.
4. Деформированная схема основной системы от принудительного смещения дополнительной связи на величину, равную единице, и соответствующая ей эпюра , построенная по таблицам прил.10, показаны на рис. 14.11, в.
5. В силу того, что стержни основной системы не загружены, так как внешняя действующая нагрузка является узловой и непосредственно, через ригель, воспринимается введённой дополнительной линейной связью, то в грузовом (рис. 14.11, г) состоянии эпюра = 0.
6. Реакции в дополнительной связи в обоих расчётных состояниях, определённые из условий равновесия вырезанного замкнутыми сечениями ригеля (рис. 14.11, д) равны: r11 = 2,625i (кН/м), R1F = – 63 (кН).
7. Каноническое уравнение в численном виде
2,625iZ1 – 63 = 0,
откуда Z1 = 63/2,625i = 24/i (м).
8. Эпюра изгибающих моментов в заданной схеме рамы будет получена как , т.к. = 0 (рис. 14.11, е). При этом эпюра изгибающих моментов на абсолютно жёстком ригеле достраивается по значениям в крайних сечениях, определённых из условий равновесия узлов.
14.3. Упрощения расчётов при использовании метода перемещений
14.3.1. Использование основной системы без постановки линейных связей
Рассмотрим свободную раму, изображённую на рис. 14.12, а. Эта рама имеет два жёстких узла A и B, способных к повороту, и два возможных линейных смещения ригелей по горизонтали, т.е. nк = 4. Основная система для расчёта методом перемещений приведена на рис. 14.12, б.
Особенностью данной рамы является возможность определения поперечных сил в стойках AB и BC непосредственно из уравнений равновесия.
Действительно, QA = ∑Fверх = – F1; QB = ∑Fверх = – F1 + qh2;
QBC = ∑Fверх = – F1 + qh2 + F3.
Данная особенность позволяет понизить порядок канонических уравнений, если применить упрощённую основную систему (рис. 14.12, в), отличающуюся от изображённой на рис. 14.12, б, отсутствием дополнительных линейных связей. Использование подобной основной системы возможно, если для стержней типа AB и BC (рис. 14.13) использовать дополнительные таблицы реакций, учитывающие смещение “плавающих” заделок не только при принудительном смещении линейных связей, но и при повороте самой связи и действии внешней нагрузки. Эти дополнительные таблицы, получаемые на основе метода сил, показаны в прил. 10 (п.п. 5 и 6) и 11 (п.п. 5 – 8).
Рассмотрим несколько примеров применения основной системы метода перемещений без постановки линейных связей.
Пример 14.4. Построить эпюру изгибающих моментов MF в раме (рис. 14.14, а).
Относительные жёсткости стержней рамы одинаковы:
стойка второго этажа и ригель первого пролёта i1 = EI/6 = i;
ригель второго пролёта i2 = 1,5EI/6 = 1,5i;
стойка первого этажа i3 = 2EI/6 = 2i.
Решение.
1. Степень кинематической неопределимости рамы в силу линейной неподвижности её узлов nк + nл =1 + 2 = 3.
В рассматриваемой раме поперечные силы в стойках могут быть определены непосредственно: Q = ∑Fверх = 12 кН. Поэтому горизонтальные дополнительные линейные связи при образовании основной системы можно не ставить (рис. 14.14, б)
2. Следовательно, каноническое уравнение метода перемещений будет единственным r11Z1 + R1F = 0.
3. Деформированная схема основной системы от принудительного поворота дополнительной связи на угол, равный единице, и соответствующая ей эпюра , построенная по таблицам прил.10, показаны на рис. 14.14, в.
При этом для ригелей рамы эпюра строится по классическим таблицам метода перемещений (прил. 10, п.п. 1 и 4), а для стоек – по таблицам, учитывающим возможность смещения концов стержней относительно друг друга (прил. 10, п. 6).
4. Эпюра ( рис. 14.14, г) в основной системе от действия внешней нагрузки также строится по двум типам таблиц: для загруженного правого ригеля рамы – по п. 4 прил.11, а для стоек – по п.6 прил. 11 при v = 1. Для верхней и нижней стойки основной системы эпюра будет одинакова, так как ввиду отсутствия горизонтальных связей на верхнее сечение нижней стойки действует горизонтальная сила F = Q = ∑Fверх = 12 кН.
5. Реакции в дополнительной связи в обоих расчётных состояниях, определённые из условий равновесия дополнительной связи (рис. 14.14, д) равны: r11 = 12i (кН·м/рад), R1F = − 84 (кН·м).
6. Каноническое уравнение в численном виде
12iZ1 − 84 = 0,
откуда Z1 = 84/12i = 7/i (рад).
7. Эпюра изгибающих
моментов в заданной схеме рамы будет
получена как
![]() .
Слагаемые приведённой формулы и результат
сложения приведены на рис. 14.15. а,
б
и в.
.
Слагаемые приведённой формулы и результат
сложения приведены на рис. 14.15. а,
б
и в.
8. Проверка равновесия жёсткого узла по полученной эпюре MF показана на рис. 14.15, г.
Пример 14.5. Построить эпюру изгибающих моментов MF в раме (рис. 14.16, а).
Относительные жёсткости стержней рамы одинаковы, так как для всех стержней, кроме консоли, i = EI/6. Консоль является статически определимой частью расчётной схемы, поэтому величина её жёсткости не имеет значения при расчёте методом перемещений.
Решение.
1. Степень кинематической неопределимости рамы в силу линейной неподвижности её узлов nк + nл =1 + 1 = 2.
В рассматриваемой раме поперечные силы в стойке могут быть определены непосредственно;
QB = ∑Fверх = 21 − 28 = − 7 кН; QA = ∑Fверх = 21 − 28 + 3,5∙6= 14 кН.
Поэтому горизонтальную дополнительную линейную связь при образовании основной системы можно не ставить (рис. 14.16, б)
2. Следовательно, каноническое уравнение метода перемещений будет единственным r11Z1 + R1F = 0.
3. Деформированная схема основной системы от принудительного поворота дополнительной связи на угол, равный единице, и соответствующая ей эпюра , построенная по табл. прил.10, показаны на рис. 14.14, в.
При этом для ригелей рамы эпюра строится по классическим таблицам метода перемещений (см. прил. 10, п.п. 1 и 4), а для стойки – по таблице, учитывающей возможность смещения концов стержня относительно друг друга (см. прил. 10, п. 5). Стойка основной системы в данной задаче является статически определимым стержнем, поэтому при отсутствии её изгиба =0
4. Эпюра (рис. 14.16, г) в основной системе от действия внешней нагрузки также строится по двум типам таблиц: для загруженного правого ригеля рамы – по п. 3 прил.11, а для стойки – по п. 6 и 7 прил. 11. Для построения полной эпюры для стойки используется принцип независимости действия сил, и эпюру получают как сумму эпюр от двух загружений (рис. 14.16, д): от горизонтальной силы F = QB = − 7 кН (см. п. 6 прил. 11, при v =1) и действующей на стержень равномерно распределённой нагрузки q = 3,5 кН/м (см. п.7 прил.11).
5. Реакции в дополнительной связи в обоих расчётных состояниях, определённые из условий равновесия дополнительной связи (рис. 14.14, е) равны: r11 = 7i (кН·м/рад), R1F = − 84 (кН·м).
6. Каноническое уравнение в численном виде
7iZ1 − 84 = 0,
откуда Z1 = 84/7i = 12/i (рад).
7. Эпюра изгибающих моментов в заданной схеме рамы будет получена как . Слагаемые приведённой формулы и результат сложения приведены на рис. 14.17. а.
8. Проверка равновесия жёсткого узла по полученной эпюре MF показана на рис. 14.17, б.
14.3.2. Учёт симметрии
При расчёте симметричных рам методом перемещений используются те же приёмы, что и при расчёте методом сил, а именно, способ группировки неизвестных и способ разложения нагрузки.
При группировке
неизвестных
перемещения симметрично расположенных
узлов основной системы можно представлять
в виде суммы (Zi
+ Zk)
и разности (Zi
− Zk)
так, чтобы эпюры
и
![]() от принудительного единичного смещения
дополнительных связей были симметричными
и кососимметричными. Тогда побочные
коэффициенты системы канонических
уравнений, определяемые по этим эпюрам
изгибающих моментов rik
= rki
= 0.
от принудительного единичного смещения
дополнительных связей были симметричными
и кососимметричными. Тогда побочные
коэффициенты системы канонических
уравнений, определяемые по этим эпюрам
изгибающих моментов rik
= rki
= 0.
Неудобство этого способа состоит в необходимости определять групповые реакции в связях, а для стержней, пересекающих оси симметрии – строить суммарные эпюры изгибающих моментов от симметричных или кососимметричных смещений дополнительных связей.
Способ разложения нагрузки более нагляден.
Например, симметричная рама, изображённая на рис. 14.18, а, имеет шесть угловых и два линейных смещения (nк = 8, рис. 14.18, б). При симметричном загружении на основании свойства 1 (см. подразд. 13.5) мы можем рассмотреть только половину схемы, в которой степень кинематической неопределимости будет nк = 2. Для той же рамы, но загруженной кососимметричной нагрузкой (рис. 14.19, а), при представлении её на основании свойства 2 в виде половины расчётной схемы степень кинематической неопределимости будет nк = 6 (рис. 14.19, б). Общее количество неизвестных метода перемещений при симметричном и кососимметричных загружениях равно полной степени кинематической неопределимости.
Ещё большее сокращение количества неизвестных можно получить в одноролётных рамах любой этажности.
В качестве примера рассмотрим симметричную двухэтажную однопролётную раму (рис. 14.20, а). Степень кинематической неопределимости данной рамы nк = 6 (рис. 14.20, б).
После разложения нагрузки 2F на основании свойств симметрии имеем:
при симметричном загружении Z3 = −Z1; Z4 = −Z2; Z5 = Z6 = 0;
при кососимметричном загружении Z3 = Z1; Z4 = Z2; Z5 ≠ 0; Z6 ≠ 0.
Таким образом, система канонических уравнений шестого порядка распалась на две подсистемы, второго порядка при симметричном и четвёртого порядка при кососимметричном загружениях.
При рассмотрении того же симметричного загружения на половине расчётной схемы (рис. 14.21, а) мы также получим систему из двух уравнений, так как для стержней АC и BD можно использовать таблицы метода перемещений, учитывающие линейную подвижность одного конца стержня относительно другого (см. прил. 10, п.п. 6,6 и прил.11, п.п. 5 – 8), основная система метода перемещений будет получена введением двух дополнительных угловых связей (рис. 14.21, б).
При рассмотрении кососимметричного загружения на половине расчётной схемы (рис.14.22. а) количество неизвестных по сравнению с рис.14.20 снижается вдвое, так как в стержнях АB и CD поперечные силы могут быть определены из уравнений равновесия, и, следовательно, можно применить основную систему без постановки линейных связей (рис. 14.22, б).
14.4. Понятие о расчёте пространственных рам
При расчёте пространственных рам методом перемещений за неизвестные принимаются, также как и для плоских рам, угловые перемещения жёстких узлов и независимые линейные перемещения всех узлов рамы.
Так как в пространственной системе каждый жёсткий узел может иметь повороты в трёх взаимно перпендикулярных плоскостях, степень кинематической неопределимости в этом случае будет определяться по формуле:
nк =3 nу + nл, (14.7)
где nу – число жёстких узлов расчётной схемы, способных к повороту при её деформации; nл – степень линейной подвижности всех узлов схемы, определяемая как степень свободы шарнирного механизма, получаемого из заданной схемы рамы путём введения во все её узлы сквозных шарниров:
nл =W = 3У – (Сф + Соп). (14.8)
Для получения основной системы во все жёсткие узлы рамы необходимо ввести пространственные “плавающие” защемления, препятствующие повороту узлов относительно трёх координатных осей, и линейные связи, не допускающие линейных перемещений узлов. В общем случае в “плавающих” защемлениях возможно возникновение трёх реактивных моментов, а в линейных связях – линейных реактивных сил.
Например, для рамы, изображённой на рис. 14.23, а, степень кинематической не определимости nк = nу + nл = 3∙4 + 4 = 16. Основная система для этой рамы представлена на рис. 14.23, б.
Канонические уравнения метода перемещения имеют тот же вид, что и для плоских рам.
Для определения коэффициентов при неизвестных и свободных членов канонических уравнений строятся эпюры изгибающих моментов от единичных принудительных смещений дополнительных связей и действия внешней нагрузки. Построение эпюр изгибающих моментов осуществляется на основе таблиц реакций (см. прил. 10 и 11), показанных при расчёте плоских рам.
При принудительном повороте дополнительных угловых связей в некоторых стержнях основной системы необходимо учитывать их кручение. Значения крутящих моментов от единичном повороте угловой связи определяются на основании (9.12) при φ =1
![]() ,
(14.9)
,
(14.9)
где i – относительная жесткость относительно какой-либо оси поперечного сечения стержня, выбранная в качестве общего множителя при расчёте; EI – изгибная жёсткость стержня относительно той же оси (i = EI/l).
Для показанной на
рис. 14.23, а
рамы эпюра
от
внешней нагрузки показана на рис. 14.24,
а деформированные состояния основной
системы и соответствующие им эпюры
моментов
,
и
![]() от двух единичных поворотов во взаимно
перпендикулярных плоскостях и одного
линейного смещения соответственно на
рис. 14.25.
от двух единичных поворотов во взаимно
перпендикулярных плоскостях и одного
линейного смещения соответственно на
рис. 14.25.
Значения реакций в дополнительных связях определяются на основании уравнений равновесия (2.36) и (2.38) для вырезанной угловой связи или части основной системы.
Эпюры изгибающих моментов в заданной расчётной схеме после определения неизвестных метода перемещений определяются на основании принципа независимости действия сил
![]() ;
;
![]() ;
(14.10)
;
(14.10)
![]() .
.
Эпюры поперечных и продольных сил строятся также, как и при расчёте пространственных рам методом сил. На отдельных этапах расчёта выполняются те же проверки, что и при расчёте плоских рам. Основными и достаточными являются деформационная и статические проверки расчёта.
Пример 14.6. Построить эпюры усилий для пространственной рамы, изображённой на рис. 14.26, а при GIк/EI = 0,5 и Iz = Iy = I. Действующая нагрузка: F = 106 кН, q = 29 кН/м.
Относительные жёсткости стержней рамы:
стержни АВ и ВЕ i1 = EI/4 = i;
стержень BD i2 = 2EI/4 = 2i;
стержень BC i3 = 4EI/4 = 4i.
Решение.
1. Степень кинематической неопределимости nк = 3, так как узел B не имеет линейных смещений. Основная система метода перемещений показана на рис. 14.26, б.
При заданной нагрузке, действующей в двух взаимно перпендикулярных плоскостях, угол поворота в третьей плоскости, перпендикулярной плоскостям действия нагрузки Z3 = 0.
2. Следовательно, канонические уравнения метода перемещений будут иметь вид r11Z1 + r12Z2 + R1F = 0;
r21Z1 + r22Z2 + R2F = 0.
Так как перемещения Z1 и Z2 возможны в двух взаимно перпендикулярных плоскостях и независимы друг от друга, в приведённых уравнениях коэффициенты r12 = r21 = 0, и уравнения примут вид
r11Z1 + R1F = 0;
r22Z2 + R2F = 0.
3. Деформированные схемы основной системы от принудительных поворотов дополнительных связей на угол, равный единице, и соответствующие ей эпюры и , построенные по таблицам прил.10, показаны на рис. 14.27, а и б.
4. Эпюра в основной системе от действия внешней нагрузки, построенная по табл. прил. 11, показана на рис. 14.28.
5. Реакции в дополнительной связи во всех расчётных состояниях определены следующим образом:
по рис. 14, 29, а
∑Mz = 0; r11 − 4i − 4i − 6i− 0,5i = 0, r11 = 14,5i (кН·м/рад);
по рис. 14, 29, б
∑My = 0; r22 − 4i −16i − 6i−0,5i = 0, r22 = 26,5i (кН·м/рад);
по рис. 14, 29, в
∑Mz = 0; R1F + 58 = 0, R1F = − 58 (кН·м);
∑My = 0; R2F + 53 = 0, R2F = − 53 (кН·м).
6. Канонические уравнения в численном виде
14,5iZ1 − 58 = 0,
26,5iZ2 − 53 = 0,
откуда Z1 = 58/14,5i = 4/i (рад); Z2 = 53/26,5i = 2/i (рад).
7. Эпюра изгибающих моментов в заданной схеме рамы будет получена как . Слагаемые приведённой формулы показаны на рис. 14.26, и 14.30, а, б. Результат сложения – эпюра MF, для наглядности, представлена в виде суммы трёх эпюр MyF, MzF и MxF = Mк (рис. 14.30, в, г и д) в общей системе координат XYZ.
8. Проверка равновесия жёсткого узла по полученной эпюре MF показана на рис. 14.30, е.
9. Эпюры QF и NF приведены на рис. 14.30, ж и з.
14.5. Принципы определения перемещений в статически неопределимых системах
Перемещения в статически определимых системах как от действия нагрузки, так и от начальных деформаций (теплового воздействия, неравномерной осадки опор и неточности изготовления стержней) можно определить по правилам определения перемещений, сформулированных в подразд. 12.4.
Например, для рамы, изображённой на рис. 14.31, а, необходимо определить вертикальное перемещение сечение k. Для определения искомого перемещения рама рассчитана от действия внешней нагрузки любым, наиболее удобным, методом (методом сил или методом перемещений), в результате чего получена эпюра MF. Затем рассмотрено вспомогательное состояние (рис. 14.31, б) от действия единичной безразмерной силы, приложенной по направлению искомого перемещения.
Величина перемещения по формуле Максвелла−Мора
![]() ,
(14.11)
,
(14.11)
где Mk – эпюра изгибающих моментов вспомогательного состояния.
Предположим, что эпюра Mk построена на основании метода сил при основной системе, показанной на рис.14.31, в. Очевидно, что она получена на основании принципа независимости действия сил как
![]() ,
(14.12)
,
(14.12)
где – эпюра от единичной силы вспомогательного состояния в статически определимой основной системе.
Подставив (14.12) в (14.11) и сделав необходимые преобразования, получим
=
![]() +
+
![]() +
+![]() +
+
+
![]() +
+
![]() .
.
В полученном выражении первые четыре интеграла должны равняться нулю на основании кинематического смысла, так как они выражают перемещения в заданной расчётной схеме от внешней нагрузки по направлениям, исключающим эти перемещения (см. деформационную проверку расчёта статически неопределимых систем).
Следовательно,
= . (14.13)
Аналогично можно показать, что
=
![]() .
(14.14)
.
(14.14)
Иными словами, для определения перемещений в статически неопределимых расчётных схемах одна из эпюр, входящих под знак интеграла Максвелла−Мора, может быть взята в любой статически определимой основной системе.
Использование формул (14.13) или (14.14) даёт существенные преимущества. Действительно, если для показанной выше рамы перемещение ΔkF определять по выражению (14.11), необходимо произвести перемножение эпюр на шести участках, а при использовании (14.13) – только на одном. Поэтому при определении вспомогательного состояния необходимо выбрать такую основную систему метода сил, чтобы эпюра была как можно проще.
Показанный на примере изгибаемой расчётной схемы вывод формулы определения перемещений в статически неопределимых системах справедлив для любых расчётных схем как плоских, так и пространственных.
Контрольные вопросы
Что называется степенью кинематической неопределимости расчетной схемы?
Как определяется степень кинематической неопределимости плоской расчетной схемы?
Как получается основная система метода перемещений?
В чем отличие основной системы метода перемещений от основной системы метода сил?
Сформулируйте смысл канонических уравнений метода перемещений.
Как определяются реакции в дополнительных связях основной системы метода перемещений от смещения этих связей и от внешнего силового воздействия?
В чем состоит особенность построения эпюр изгибающих моментов в стержнях основной системы метода перемещений от смещения дополнительных связей и внешнего силового воздействия?
Каков порядок расчета балок и рам методом перемещений?
На каком этапе расчета методом перемещений учитывается влияние внешней узловой нагрузки?
Как производится проверка правильности расчета, произведенного на основе метода перемещений?
В каких случаях можно использовать основную систему метода перемещений без постановки линейных дополнительных связей?
Какие упрощения расчета возможны при расчете методом перемещений симметричных рам? В чем состоят эти упрощения?
Сформулируйте основные особенности расчета методом перемещений пространственных рам.
Как определяются перемещения в статически неопределимых расчетных схемах?
Глава 15 основы динамики сооружений
15.1. Общие положения
Динамика сооружений – часть строительной механики, рассматривающая вопросы расчёта сооружений на динамические нагрузки.
Динамические нагрузки в отличие от статических изменяются по величине, направлению или положению в относительно малые промежутки времени.
Различают следующие основные виды динамических нагрузок.
Вибрационная нагрузка – это нагрузка, значения которой изменяются периодически по определённому закону. Она может быть как прерывной, так и непрерывной.
Ударная нагрузка (удар в определённом месте сооружения) характерна резким изменением скорости ударяемого тела в короткий отрезок времени.
Подвижная нагрузка – нагрузка, положение которой на сооружении меняется с достаточно большой скоростью.
Кратковременные нагрузки (импульсы) характеризуются практически мгновенным действием.
Сейсмические нагрузки – результат беспорядочного движения почвы, толчков и ударов при землетрясениях.
Вызываемые такими нагрузками перемещения и деформации как самого сооружения, так и его элементов также будут изменяться во времени, т.е. совершать движения.
В широком смысле динамика является учением о движении твёрдых тел в зависимости от сил, к ним приложенных. В основе динамики лежат три основные закона, сформулированные И.Ньютоном (1686 г.)
Первый закон (закон инерции). Если на материальную точку не действуют никакие силы, то она находится в покое, либо совершает равномерное прямолинейное движение.
Свойство тела сохранять своё механическое состояние называют инерцией. Отсюда и название этого закона.
Второй закон (закон зависимости между силой и ускорением). Сила, приложенная к материальной точке массой m, сообщает ей ускорение, имеющее направление силы и величину, пропорциональную величине силы.
F = mÿ(t), (15.1)
Равенство (15.1) в силу его важности называют основным уравнением динамики. Из этого уравнения видно, что для сообщения одного и того же ускорения точке большей массы необходима большая сила. Следовательно, масса точки есть мера её противодействия изменению скорости, или, иначе, мера инерции.
Третий закон (закон равенства действия и противодействия). Всякое действие вызывает равное и противоположно направленное противодействие. Из статики (см. подразд. 2.1) нам уже известен этот закон как аксиома 5.
Любое сооружение можно рассматривать как совокупность материальных точек, т.е. как материальную систему. Для любой материальной системы, как было показано в подразд. 8.2, всегда можно найти центр тяжести с координатами xC, yC, zC, который одновременно является и центром инерции системы материальных точек.
Можно доказать, что центр инерции материальной системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все действующие на систему силы. Это положение называется законом движения центра инерции.
Этот закон позволяет во многих случаях заменить рассмотрение движения всей материальной системы движением её центра инерции.
На основании второго закона Ньютона (15.1) и закона движения центра инерции получают дифференциальные уравнения движения центра тяжести тела:
![]() ;
;
![]() ;
;
![]() .
(15.2)
.
(15.2)
Итак, все точки материальной системы, каковой является расчётная схема, совершают движения, изменяющиеся во времени, т.е. характеризуются чередованием возрастания и убывания расстояний отдельных точек системы от их положения в некоторый зафиксированный момент времени, а именно при отсутствии динамических нагрузок. Такие движения в технике называют колебаниями.
Различают следующие виды колебаний.
Свободные колебания – это колебания системы, выведенной из начального равновесного состояния каким- либо начальным возмущением.
Вынужденные колебания – это колебания, вызванные внешней возмущающей силой и поддерживаемые ею в течение определённого отрезка времени.
Для получения уравнений движения масс в динамике сооружений применяются три основных метода.
Первый метод использует непосредственно дифференциальные уравнения движения (15.2), составленные для каждой массы системы. Все массы системы при этом предполагаются освобождёнными от наложенных на них связей, действия которых на массы заменяются реакциями этих связей.
Второй метод называется методом кинетостатики и основан на использовании принципа Ж.Л.Даламбера.
Покажем сущность этого принципа применительно к материальной точке. Выражение (15.1) запишем в виде
F − mÿ(t)= 0 или F + [− mÿ(t)]= 0. (15.3)
Обозначим J = − mÿ(t). (15.4)
Подставив (15.4) в 15.3), получим
F + J= 0. (15.5)
В выражении (15.5) F представляет собой равнодействующую всех сил. действующих на материальную точку, а силу J называют силой инерции.
Сила инерции по модулю равна mÿ(t) и направлена в сторону, противоположную ускорению ÿ(t).
Выражение (15.5) представляет собой принцип Даламбера для материальной точки: при движении материальной точки в каждый момент времени действующие на неё активные силы, реакции наложенных на неё связей и силы инерции уравновешивают друг друга.
Принцип Даламбера легко распространить на систему материальных точек, т.е. на материальное тело и систему материальных тел.
Таким образом, согласно принципу Даламбера уравнение движения можно рассматривать как уравнение равновесия, что позволяет задачу динамики для каждого момента времени по форме решения свести к статической задаче.
Третий метод называется энергетическим. Он основан на законе сохранения механической энергии,
В связи с ограниченностью материала, приводимого в данном издании, мы будем использовать только второй метод.
Поскольку в основе динамического расчёта сооружений лежит учёт инерционных сил, необходимо знать расположение масс в рассматриваемом сооружении. С этой точки зрения в динамике сооружений два основных типа расчётных схем: системы с распределённой массой и системы с сосредоточенными массами.
В расчётных схемах с распределёнными массами наряду с геометрическими характеристиками элементов необходимо знать законы распределения масс по длинам элементов.
В расчётных схемах с сосредоточенными массами каждый элемент рассматривается как невесомый стержень с заданными геометрическими характеристиками и заданным точечным расположением масс.
Основным понятием динамики сооружений является степень свободы масс Wm, под которым понимается число независимых геометрических параметров, определяющих положение масс в любой момент времени
В случае расчётной схемы с распределёнными массами мы имеем бесконечное число степеней свободы масс. В расчётных схемах с сосредоточенными массами необходимо определить число их степеней свободы в начале динамического расчёта.
В плоских стержневых расчётных схемах, рассматриваемых в настоящей главе, при определении степени свободы сосредоточенных масс вводятся следующие допущения:
1. Сосредоточенная масса считается точечной, т.е. имеет на плоскости две степени свободы, определяемые двумя линейными перемещениями; углом поворота сосредоточенной массы на плоскости пренебрегают.
2. Как и ранее пренебрегают продольными деформациями в изгибаемых стержнях и изменением их длины за счёт искривления при изгибе.
Так для невесомой балки с одной сосредоточенной массой (рис. 15.1, а) степень свободы Wm =1, так как положение массы определяется одним перемещением y1.
Для консольной балки с осью ломаного очертания (рис. 15.1, б) и двумя сосредоточенными массами m1 и m2 степень свободы равна трём, так как масса m1 имеет два линейных смещения, а масса m2 – только одно, горизонтальное.
В консольной ферме (рис. 15.1, в) одна сосредоточенная масса за счёт продольных деформаций стержней фермы имеет две степени свободы.
Для упрощения подсчёта степеней свободы сосредоточенных масс расчётной схемы удобно использовать следующий приём. По направлению возможных перемещений сосредоточенных масс мысленно устанавливают линейные связи, препятствующие движению этих масс. Наименьшее число линейных связей, позволяющее закрепить все сосредоточенные массы расчётной схемы, и будет определять число степеней свободы.
Так, для рамы, изображённой на рис. 15.1, г, для закрепления пяти сосредоточенных масс от возможных смещений необходимо поставить четыре линейных связи. Следовательно, степень свободы масс данной расчётной схемы
Wm= 4.
При выборе динамической расчётной схемы, а именно, при определении числа степеней свободы масс, необходимых для достоверного расчёта, необходим анализ исходной информации о рассматриваемом сооружении.
Например, для сооружения башенного типа (рис. 15.2, а) часто достаточно представить расчётную схему в виде консольного стержня с точечной массой, сосредоточенной на его конце. Из анализа динамического поведения многоэтажного здания башенного типа с учётом того, что суммарная масса перекрытий и покрытия намного превосходит массу стен, можно использовать расчётную схему консольного стержня с сосредоточенными массами в уровне перекрытий здания (рис. 15.2, б).
Как правило, в большинстве инженерных расчётов действительная распределённая масса сооружения приводится к точечным.
15.2. Колебания упругих систем с одной степенью свободы
15.2.1. Свободные колебания
Рассмотрим невесомый консольный стержень с точечной массой, расположенной на конце этого стержня (рис. 15.3, а). При свободных колебаниях на массу m, отклонившуюся от первоначального положения на величину y(t), в любой момент времени будут действовать восстанавливающая сила R, сила неупругого сопротивления (диссипативная) S и сила инерции J (рис. 15.3, б).
Восстанавливающая сил R – это сила упругого сопротивления, которой рассматриваемый стержень действует на массу, стремясь вернуть её в исходное положение. В упругой системе восстанавливающая сила прямо пропорциональна отклонению массы y(t) и определяется выражением
R = r11 y(t), (15.6)
где r11 – коэффициент пропорциональности или коэффициент жёсткости конструкции, зависящий от её упругих свойств. Коэффициент жёсткости – сила, которую необходимо приложить к конструкции по направлению колебания массы, чтобы вызвать её перемещение, равное единице. Коэффициент жёсткости есть величина, обратная податливости δ11 (рис. 15.3, в)
r11 = 1/ δ11. (15.7)
Диссипативная сила S – сила, учитывающая неупругие сопротивления движению массы:
силы внутреннего трения, возникающие из-за вязкости или неполной упругости материала конструкции;
силы трения в местах соединения элементов конструкции и на опорах;
силы сопротивления окружающей среды, в которой происходят колебания.
Точный учёт всех перечисленных факторов ввиду их разнообразия и неопределённости не представляется возможным. Поэтому для их учёта приняты различные гипотезы, из которых наиболее распространена гипотеза Кельвина-Фойгта. По этой гипотезе, называемой гипотезой вязкого трения, диссипативная сила принимается пропорциональной скорости колебаний
S
= β![]() (t),
(15.8)
(t),
(15.8)
где β – коэффициент пропорциональности или коэффициент сопротивления – величина, определяемая экспериментально и характеризующая силу вязкого трения при скорости (t) =1.
Выделим массу со всеми действующими на неё силами и составим уравнение равновесия (сумму проекций на ось, параллельную движению массы). В результате получим
R + S − J = 0. (15.9)
Подставив в (15.8) выражения (15.4), (15.6) и (15.7), получим
![]() .
.
Разделив данное выражение на m и введя обозначения
2k = β/m и ω2 = r11/m, (15.10)
получим
![]() .
(15.11)
.
(15.11)
Выражение (15.11) называется дифференциальным уравнением движения точечной массы при свободных колебаниях.
С в о б о д н ы е н е з а т у х а ю щ и е к о л е б а н и я
Для большого числа инженерных расчётов силами неупругого сопротивления пренебрегают. Тогда в выражении (15.11) величина 2k = 0 и само дифференциальное уравнение движения принимает вид
![]() .
(15.12)
.
(15.12)
Решение однородного дифференциального уравнения (15.12) известно из курса высшей математики и имеет вид
![]() .
(15.13)
.
(15.13)
Скорость колебаний массы m определяется первой производной по времени от полученного уравнения движения (15.13)
![]() .
(15.14)
.
(15.14)
Произвольные
постоянные A
и B
определим из начальных условий, в
качестве которых примем: при
![]() (
v0
– начальная скорость колебаний).
Подставив принятые начальные условия
в (15.13) и (15.14), получим A
= 0, B
= v0/ω,
а уравнение движения (15.13) примет вид
(
v0
– начальная скорость колебаний).
Подставив принятые начальные условия
в (15.13) и (15.14), получим A
= 0, B
= v0/ω,
а уравнение движения (15.13) примет вид
![]() .
(15.15)
.
(15.15)
Из (15.15) следует, что при отсутствии диссипативных сил масса m будет совершать простые гармонические незатухающие колебания. График этой функции показан на рис. 15.4. Из графика видно, что наибольшие отклонения массы от первоначального положения равны постоянной величине a = ν0/ω, называемой амплитудой колебаний. Удвоенная амплитуда называется размахом колебаний.
Время T в секундах, за которое масса совершает полный цикл колебаний, называется периодом колебаний. Из графика видно, что
T = 2π/ω. (15.16)
Число полных колебаний в единицу времени называется частотой колебаний. Из (15.16) получаем ω=2π/T (c-1) – число колебаний за время 2π секунд. Поэтому величина называется круговой частотой колебаний.
Круговая частота на основании обозначения (15.10) с учётом (15.7) может быть определена по формуле
 .
(15.17)
.
(15.17)
Число колебаний в одну секунду измеряется в Гц (герцах) и может быть выражена через круговую частоту или период колебаний:
![]() .
(15.18)
.
(15.18)
В инженерной практике нередко используется техническая частота колебаний – число колебаний в минуту. Она также может быть выражена через круговую частоту или период колебаний:
![]() .
(15.19)
.
(15.19)
Выражения (15.16) – (15.19) называются параметрами колебаний, основными из которых являются круговая частота и период колебаний.
С в о б о д н ы е з а т у х а ю щ и е к о л е б а н и я
График, приведённый на рис.15.4, показывает, что невесомый стержень с одной массой, начав колебаться, будет продолжать эти колебания неограниченное время без воздействия каких-либо сил. В действительности этого не происходит. Любая упругая система, выведенная из начального состояния равновесия, поколебавшись, останавливается. Причиной этого является действия сил сопротивления S.
Если при рассмотрении свободных колебаний принять те же начальные условия, т.е. при , то дифференциальное уравнение движения (15.11) точечной массы, учитывающее влияние сил сопротивления будет иметь следующее решение
![]() .
(15.20)
.
(15.20)
График функции (15.20) показан на рис. 15.5.
Здесь:
− начальная амплитуда колебаний a0= v0/ω1;
− круговая частота при учёте затухания
![]() .
(15.21)
.
(15.21)
Согласно формуле (15.20) теоретически полное затухание наступит при t → ∞, что противоречит действительности. Это противоречие свидетельствует об одном из недостатков принятой гипотезы вязкого трения.
С целью оценки скорости затухания колебаний рассматриваются две соседние амплитуды по графику (15.5) и вычисляется их отношение
 .
.
В качестве меры затухания колебаний берётся не само отношение соседних амплитуд, а его натуральный логарифм, т.е.
![]() .
(15.22)
.
(15.22)
Эта величина, характеризующая скорость затухания, называется логарифмическим декрементом затухания, а величина k = 0,5 β/m – коэффициентом затухания. Величина декремента является постоянной, не зависящей от времени. Она учитывает характеристики конструкции и окружающей среды. Так как этих характеристик достаточно много, то коэффициент затухания k определяется экспериментально, путём замеров амплитуд колебаний специальными приборами.
В справочной литературе для оценки затухания приводятся значения коэффициентов поглощения ψ= 2 kT. Значения этих коэффициентов для разных материалов и различных амплитуд инерционных сил приведены в табл. 15.1.
Таблица 15.1
Значения коэффициентов поглощения ψ
Амплитуда инерционной силы, кН |
Железобетон |
Кирпичная кладка |
Дерево |
Сталь прокатная |
< 1 |
0,314 |
0,251 |
0,188 |
0,063 |
≥ 1 |
0,628 |
0,503 |
0,314 |
0,157 |
Значения коэффициента затухания k для большинства строительных конструкций, колебания которых происходят в окружении воздушной среды, не очень велики, поэтому чаще всего (особенно в инженерных расчётах) частоты свободных колебаний определяются без учёта диссипативных сил, т.е. ω1 ≈ ω.
При затухающих колебаниях их период на основании (15.16) T = 2π/ω1, поэтому логарифмический декремент затуханий
![]() ,
,
откуда, пренебрегая γ2 как величиной второго порядка малости, получим
 .
.
Пример 15.1. Определить круговую и техническую частоты, а также период колебаний системы с одной степенью свободы, показанной на рис. 15.6, а. Жёсткость стержней EI = 5400 кН·м2, величины массы m = 0,25 т.
Решение.
1. Масса m может совершать только вертикальные колебания. Вспомогательное состояние расчётной схемы для определения податливости по направлению колебания массы показано на рис. 15.6, б, соответствующая ему эпюра изгибающих моментов M1 – на рис. 15.6, в.
2. Податливость
![]() (м/кН).
(м/кН).
3. Круговая частота свободных колебаний по формуле (15.17)
![]() = 200 с-1.
= 200 с-1.
4. Период колебаний T = 2π/ω = 2π/200 = 0,031 с.
5. Техническая частота n = 60/T = 60/0,031= 1909, 9 кол/мин.
Пример 15.2. Определить круговую частоту и период свободных колебаний сосредоточенного груза массой m = 3 т, расположенного на конце консоли статически неопределимой рамы (рис.15.7, а). Жёсткость стержней рамы постоянна и равна EI = 12600 кН·м2.
Решение.
1. Степень свободы сосредоточенной массы Wm = 1, так как при принятых допущениях она может совершать колебания только по вертикали.
2. Вспомогательное состояние для определения податливости рамы по направлению колебания массы показано на рис. 15.7, б.
3. Выбираем метод решения для определения усилий в представленном вспомогательном состоянии.
Степень статической неопределимости рамы nc = 3К – Ш = 3·1 – 1 =2.
Степень кинематической неопределимости nк = nу – nл = 1 – 0 = 1.
Так как nк < nc , то расчёт производим методом перемещений.
4. Каноническое
уравнение метода перемещений r11Z1
+
r1F
= 0. Основная система метода и эпюра
изгибающих моментов
![]() грузового состояния показаны на рис.
15.7, в.
грузового состояния показаны на рис.
15.7, в.
Относительные жёсткости стержней рамы:
ригеля i1 = EI/4 = i; стойки i2 = EI/3 = 4i/3.
5. Деформированная схема основной системы от принудительного поворота дополнительной связи на единичный угол и соответствующая ей эпюра изгибающих моментов показаны на рис. 15, 7, г.
6. Реакции в дополнительной связи, определённые по эпюрам и , равны r11 = 8i (м/рад) и r1F = 2 (м). Тогда неизвестное канонического уравнения Z1= −r1F/r11= − 0,25/i (рад).
7. Эпюра изгибающих
моментов вспомогательного состояния
(рис. 15.7, б)
![]() показана на рис. 15.7, д.
показана на рис. 15.7, д.
8. Для определения податливости по направлению колебания массы на основании положений § 14.5 выберем статически определимую основную систему и в ней построим вспомогательную эпюру изгибающих моментов (рис. 15.7, е) от действия единичной силы, приложенной по направлению колебания массы.
Тогда
![]() (м/кН).
(м/кН).
9. Круговая частота свободных колебаний по формуле (15.17)
![]() = 30 с-1.
= 30 с-1.
10. Период колебаний T = 2π/ω = 2π/30 = 0,209 с.
Пример 15.3. Определить круговую частоту свободных колебаний массы m, расположенной в крайнем правом узле консольной статически неопределимой фермы (рис. 15.8, а). Продольная жёсткость стержней фермы EA постоянна.
Решение.
1. Степень свободы массы m Wm =1, так как узел, в котором она расположена, закреплён горизонтальной линейной связью. Поэтому масса m может совершать только вертикальные колебания.
2. Вспомогательное состояние фермы при действии единичной силы, приложенной по направлению колебания массы, показано на рис. 15.8, б.
3. Степень статической неопределимости фермы
nc = C – 2У = (6 + 5) - 2·5 = 1.
4. Каноническое
уравнение метода сил
![]() .
.
(коэффициент при неизвестном и свободный член канонического уравнения отмечены чертами сверху, чтобы отличить эти величины от значений податливостей, используемых при динамических расчётах).
5. Основная система, принятая для расчёта, показана на рис. 15.8, в.
6. Расчётные эпюры
и
![]() вспомогательного и грузового состояний
основной системы метода сил показаны
на рис. 15.9, а
и б
соответственно.
вспомогательного и грузового состояний
основной системы метода сил показаны
на рис. 15.9, а
и б
соответственно.
7. Коэффициент при неизвестном и свободный член канонического уравнения вычисляем по формуле Максвелла – Мора.
![]() (м/кН);
(м/кН);
![]() (м/кН).
(м/кН).
8. Решаем каноническое
уравнение
![]() ,
находим усилия от действия X1
(рис. 15.9, в)
и строим эпюру продольных сил
,
находим усилия от действия X1
(рис. 15.9, в)
и строим эпюру продольных сил
![]() (рис. 15.9, г).
(рис. 15.9, г).
9. Определяем податливость по направлению колебания массы, используя упрощения при определении перемещений в статически неопределимых системах (см. подразд. 14.5).
![]() (м/кН).
(м/кН).
10. Круговая частота свободных колебаний по формуле (15.17)
![]() ( с-1).
( с-1).
15.2.2. Вынужденные колебания при действии вибрационной нагрузки
Как было указано выше, вынужденными называются колебания, вызванные переменными во времени внешними воздействиями. Наиболее часто в инженерной практике приходится иметь дело с гармоническим воздействием внешней нагрузки
![]() ,
(15.23)
,
(15.23)
где F – амплитудное значение возмущающей силы, кН;
θ – круговая частота изменения возмущающей силы.
К вертикальной составляющей вида (15.23) сводится, например, действие установленного на сооружении двигателя из-за неуравновешенности ротора, масса m которого имеет относительно оси вращения эксцентриситет e. Во время вращения ротора будет возникать центробежная сила инерции
Jц = meθ2,
где θ – угловая скорость (число оборотов ротора в 2π секунд).
Вертикальная составляющая центробежной силы и будет представлять амплитудное значение возмущающей силы (15.23), т.е. F = Jц.
Вибрационная нагрузка является опасной для строительных конструкций по следующим причинам:
1. Эффект действия вибрационной нагрузки зависит не только от её величины (амплитудного значения), но и от периода её изменения. Малая по величине нагрузка с одним периодом может привести к разрушению конструкции, в то время как нагрузка большей величины, но с другим периодом, может оказаться безопасной и близкой к статическому воздействию.
2. Действие вибрационной нагрузки достаточно сложно локализовать. Наибольший эффект от её действия может сказаться не там, где она приложена, а в удалённых местах и даже в других сооружениях. Причиной этого является особенность каждого материального тела, в том числе и грунтов, воспринимать, совершать и распределять колебания.
Кроме этого, вибрационная нагрузка при определённых параметрах может оказывать вредное воздействие на людей и на безупречную работу машин и механизмов, расположенных в сооружении.
В выражении (15.23) может быть представлена не только сосредоточенная сила F, но и распределённая нагрузка, момент. При действии нескольких видов вибрационных нагрузок с целью упрощения расчёта обычно принимается, что все они во времени изменяются по одному и тому же закону и отличаются лишь амплитудными значениями. Если же это допущение не выполняется, производится расчёт от каждого воздействия в отдельности, а затем на основании принципа независимости действия сил результаты суммируют для наиболее неблагоприятных моментов времени.
Рассмотрим действие на систему с одной степенью свободы сосредоточенной возмущающей силы в форме (5.23), приложенной по направлению колебания массы (рис. 15.10)
В этом случае динамическое уравнение равновесия (15.9) примет вид:
R + S − J −Fsinθt= 0.
Подставив в приведённое уравнение равновесия значения сил (15.4), (15.6), (15.7) и обозначения (15.10), получим
![]() .
(15.24)
.
(15.24)
Уравнение (15.24) является линейным, неоднородным и называется дифференциальным уравнением движения точечной массы при действии на неё вибрационной нагрузки.
Решение дифференциального уравнения (15.24) складывается из решения однородного дифференциального уравнения (15.11) в форме (15.20) и частного решения
![]() .
(15.25)
.
(15.25)
Произвольная постоянная C определяется при тех же начальных условиях, т.е. при , и имеет следующее значение
 .
(15.26)
.
(15.26)
Из под знака корня
знаменателя (15.26) вынесем величину
![]() .
Учтя, что на основании (15.17)
.
Учтя, что на основании (15.17)
![]() ,
получим
,
получим
 .
.
В полученном выражении величина δ11F = Δ1F есть перемещение массы от статического действия амплитудного значения возмущающей силы, и данное выражение можно переписать в виде C = μ Δ1F, и уравнение движения точечной массы (15.25) примет вид
![]() .
(15.27)
.
(15.27)
Первый член полученного уравнения выражает свободные затухающие колебания, а второй – вынужденные. Как было показано выше, свободные колебания быстро затухают благодаря диссипативным силам, и тогда устанавливаются вынужденные колебания с частотой θ.
Во второй член уравнения (15.27) входят следующие величины: ε – сдвиг фазы вынужденных колебаний по отношению к колебаниям возмущающей силы, характеризующий величину опережения
![]() ,
,
μ – динамический коэффициент гармонической нагрузки, показывающий, во сколько раз динамическое действие превышает статическое действие её амплитудного значения, а именно yдин = μ Δ1F.
В силу принятых в § 4.3 гипотез и допущений соотношение между результатами динамического расчёта и результатами от статического действия амплитудного значения нагрузки справедливо для любых расчётных величин, т.е. Mдин = μ MF; Qдин = μ QF; Nдин = μ NF; σдин = μ σF и т.д.
Поскольку в инженерных расчётах обычно принимают, что ω1 ≈ ω, выражение для динамического коэффициента записывают в виде:
 либо
либо
 .
(15.28)
.
(15.28)
Как видно из выражений (15.28) значение динамического коэффициента зависит от соотношения частот θ/ω. На рис.15.11 приведён график зависимости динамического коэффициента от соотношения при разных значениях декремента затухания. Этот график показывает, что диссипативные силы значительно влияют на величину динамического коэффициента в зоне резонанса, т.е. при θ = ω или близких к этому соотношениях.
При совпадении частот (θ = ω) из формул (15.28) получается, что
![]() .
(15.29)
.
(15.29)
Наибольшее значение динамический коэффициент достигает при
![]() ,
тогда
,
тогда
 .
(15.30)
.
(15.30)
Однако разница между результатами по формулам (15.29) и (15.30) очень мала.
Из (15.29) видно, что при резонансе амплитуда вынужденных колебаний обратно пропорциональна логарифмическому декременту затухания. Сдвиг фазы колебаний по отношению к возмущающей силе составляет при этом ε = − 0,5π , т.е. 0,25 периода.
Так как проектирование строительных конструкций при установившихся колебаниях не допускает резонанса, то в первом приближении их динамический расчёт проводят без учёта диссипативных сил, те. при k = 0.
Тогда формула (15.28) примет вид
 .
(15.31)
.
(15.31)
График динамического коэффициента, вычисляемого по формуле (15.31), показан на рис. 15.12.
Однако эта формула оказывается недостаточно точной в области , близкой к резонансу, в которой особенно велико влияние затухания. При равенстве частот θ = ω формула (15.31) приводит к значениям μ= ± ∞, которые в действительности не могут быть достигнуты.
При θ > ω величина μ по формуле (15.31) становится (пунктирная линия на рис. 15.8) отрицательной. Это означает, что колебания возмущающей силы и самой массы происходят в противоположных направлениях.
Так как при резонансе происходит резкое увеличение перемещений и усилий в элементах конструкции, во избежании этого при проектировании необходимо обеспечить, чтобы частоты свободных и вынужденных колебаний отличались друг от друга на 25 – 30 %.
Пример 15.4. Произвести проверку прочности наиболее опасного сечения и определить максимальный прогиб в балке (рис. 15.13) при работе электродвигателя массой m = 3 т, совершающего 500 об/мин. Масса неуравновешенных частей двигателя m1 = 0,146 т, их эксцентриситет относительно оси вращения e = 0,0228 м. Балка изготовлена из стали марки С245 (Ry = 245 МПа). Сечение балки – двутавр № 30 (Iz = 7080 см4, Wz = 472 см3), γс = 1.
Решение.
Жёсткость балки при изгибе EI = 2,06·108·7080·10-8 = 14 585 кН·м2.
Круговая частота вынужденных колебаний
θ = nπ/30 = 500π/30 = 52,36 с-1.
3. Амплитуда возмущающей силы
F = m1eθ2 = 0,146·0,0228·52,362 =10 кН.
4. Вес электродвигателя G = mg = 3,5·9,81 = 34,335 кН.
5. Податливость балки по направлению колебания массы и наибольший изгибающий момент в среднем сечении (рис. 10.7)
![]() = 9,14·10-5
м/кН;
= 9,14·10-5
м/кН;
![]() м.
м.
6. Круговая частота свободных колебаний (15.17)
![]() = 55,9 с-1.
= 55,9 с-1.
7. Соотношение частот
θ/ω = 52,36/55,9 = 0,9367; (θ/ω)2 = 0,8773.
8. Динамический коэффициент (15.31) μ = 1/(1− 0,8773) = 8,15.
9. Прогибы балки в середине пролёта
от веса двигателя Δ1G = δ11G = 9,14·10-5·34,335 = 312,45·10-5 м;
статический от амплитуды возмущающей силы
Δ1F = δ11F = 9,14·10-5·10 = 93,77·10-5 м;
динамический прогиб yдин = μ·Δ1F = 8,15·91,4·10-5 = 744,9·10-5 м;
полный прогиб
f = Δ1G + yдин = (312,45+744,9)10-5 = 1057,35·10-5 м = 10,57 мм.
10. Наибольший изгибающий момент в балке на основании принципа независимости действия сил
Mmax = MG + Mдин = MG + μMF=M1G + μM1F= M1(G + μF) =
= 1(34,335 +8,15·10) = 115,835 кНм.
Наибольшее нормальное напряжение в среднем сечении балки
σmax = Mmax /Wz= 115,835/472·10-6 =
=0,2454·106 кН/м2 =245,4 МПа > γсRy = 245 МПа.
Перенапряжение составляет 0,4·100/245 = 0,16 % <[1%], что вполне допустимо.
Пример 15.5. Двигатель весом G =28 кН установлен на консоли балки (рис.15.14, а). Число оборотов двигателя n = 300 об/мин. При вращении двигатель создаёт возмущающую силу F(t) = 7sinθt кН. Определить максимальный прогиб консоли и построить расчётную эпюру изгибающих моментов, если балка изготовлена из двутавра № 50 (Iz = 39727 см4).
Решение.
Жёсткость балки при изгибе EI = 2,06·108·39727·10-8 = 81837,6 кН·м2.
Круговая частота вынужденных колебаний
θ = nπ/30 = 300π/30 = 31,4 с-1.
3. Масса электродвигателя m = G/ g = 28/9,81 = 2.854 т.
4. Вспомогательное состояние для определения податливости балки по направлению колебания массы m и соответствующая ей эпюра изгибающих моментов M1 показаны на рис.15.14, б.
5. Податливость балки по направлению колебания массы
![]() =
=
= 13,396·10-5 м/кН.
6. Круговая частота свободных колебаний (15.17)
![]() = 51,14 с-1.
= 51,14 с-1.
7. Соотношение частот
θ/ω = 31,4/51,14 = 0,614; (θ/ω)2 = 0,377.
8. Динамический коэффициент (15.31) μ = 1/(1− 0,377) = 1,605.
9. Прогибы консоли:
от веса двигателя Δ1G = δ11G = 13,396·10-5·28 = 375,09·10-5 м;
статический от амплитуды возмущающей силы
Δ1F = δ11F = 13,396·10-5·7 = 93,77·10-5 м;
динамический прогиб yдин = μ·Δ1F = 1,605·93,77·10-5 = 150,5·10-5 м;
полный прогиб
f = Δ1G + yдин = (375,09+150,5)10-5 = 525,59·10-5 м = 5,26 мм.
10. Расчётную эпюру изгибающих моментов строим на основании принципа независимости действия сил (рис. 15.14, в).
Mрасч = MG ± Mдин = MG ± μMF=M1G ± μM1F= M1(G ± μF) = M1(28 ± 11,235).
Поскольку динамическая эпюра изгибающих моментов M(t) = Mдин sinθt изменяется по тому же гармоническому закону, что и возмущающая сила, то на рис. 15,14, в показаны значения расчётной эпюры моментов для двух состояний M(t): при sinθt =1 (сплошная линия Mрасч = 39,235 M1) и при sinθt = −1 (пунктирная линия Mрасч = 16,765 M1).
15.2.3. Действие ударной нагрузки
При ударе происходит передача кинетической энергии ударяющего груза упругой системе, сопровождающаяся деформацией последней и возникновением равных между собой сил взаимодействия груза и упругой системы. Удар может быть продольным, когда ударяющий груз действует вдоль оси элемента расчётной схемы, и поперечным, если удар происходит перпендикулярно оси элемента.
Рассмотрим явление удара при следующих допущениях:
1. при ударе в элементе расчётной схемы возникают только упругие деформации;
2. удар считается неупругим, т.е. ударяющее тело не отскакивает после удара, а продолжает перемещаться вместе с ударяемым телом как одно целое;
Предположим, что
груз весом G
падает на невесомую балку с высоты h.
Скорость падения груза, как известно
из курса физики, равна
![]() ,
откуда h
= v2/2g.
,
откуда h
= v2/2g.
Действие ударяющего груза на балку выразим через эквивалентную силу Pэкв. Очевидно, что тогда динамическое перемещение места удара будет yдин = δ11Pэкв, где δ11− податливость балки в направлении удара.
Выразив величину эквивалентной силы через динамическое перемещение, получим Pэкв = yдин / δ11.
Величина полной работы падающего груза
Ту = G(h + yдин).
Полученная работа переходит в потенциальную энергию деформации ударяемой конструкции, величина которой
U
= 0,5Pэкв
yдин
= 0,5![]() /δ11.
/δ11.
Приравняв на основании (12.14) и (12.15) Ту = U, получим
G(h + yдин) = 0,5 /δ11 или −2δ11G yдин−2δ11Gh = 0,
где δ11G = Δ1G – статический прогиб места удара от статического действия груза G.
Решив полученное квадратное уравнение относительно yдин, получим
 .
(15.32)
.
(15.32)
Выражение в скобках формулы (15.32) показывает, во сколько раз результат ударного (динамического) действия груза больше его статического действия, и, следовательно, является динамическим коэффициентом при ударе, т.е.
 .
(15.33)
.
(15.33)
Таким образом, Рэкв= μG, yдин = μΔ1G. Эти же соотношения между статическим и динамическим действием падающего груза в силу допущения о справедливости закона Гука в пределах упругости сохраняются для любых усилий, напряжений и перемещений в сечениях расчётной схемы.
Определив силу удара Рэкв, можно производить обычный статический расчёт любой расчётной схемы, считая Рэкв обычной статической нагрузкой.
Если в формуле (15.33) положить h = 0, т.е. нагрузку приложить сразу (случай внезапного приложения нагрузки), величина динамического коэффициента μ = 2. Это означает, что внезапно приложенная нагрузка вызывает вдвое большие деформации и напряжения, чем при статическом действии той же нагрузки.
При наличии на сооружении в месте удара сосредоточенной массы m при массе падающего груза m1, статический прогиб от веса обеих масс будет уже равным
![]() .
.
Подставляя в (15.33) Δпр вместо Δ1G, получим
 .
(15.34)
.
(15.34)
Равномерно распределённая масса m (т/м) конструкции приводится к сосредоточенной в месте удара. В таблице 15.2 приведены значения массы mпр, при приведении распределённой массы к месту удара С.
Таблица 15.2
Приведение равномерно распределённой массы к месту удара

Пример 15.6. Определить силу удара груза G1 = 2 кН, падающего с высоты h = 0,2 м на железобетонную балку (рис. 15.15) пролётом l = 6,0 м. Балка изготовлена на бетоне класса В30 (Eb= 32,5·103 МПа, Iz= 36·10-4 м4). Собственный вес балки G = 20 кН.
Решение.
Масса падающего груза m1 = G1/g = 2/9,81= 0,204 т.
Масса балки, приведённая к месту удара (табл. 15. 2, п.1)
mпр = 0,493G/g = 0.493·20/9.81 = 1.005 т.
Статический прогиб от действия падающего груза (рис. 10.7)
![]() = 7,69·10-5
м.
= 7,69·10-5
м.
4. Соотношения масс m1/(m1 +m) = 0,204/(0,204+1,005) = 0,1687.
5. Значение динамического коэффициента (15.34)
![]() = 30,64.
= 30,64.
6. Эквивалентная сила удара Pэкв= μG1 = 30,64·2 =61,28 кН.
7. Если пренебречь собственной массой балки, то динамический коэффициент (15.33) и сила удара получаются по расчёту значительно большими:
![]() = 73,13; Pэкв=
73,13·2 =146,26 кН.
= 73,13; Pэкв=
73,13·2 =146,26 кН.
Таким образом, сила удара груза, даже при падении с небольшой высоты, оказывается значительно больше, чем вес самого груза. При этом, как видно из формул (15.33) и (15.34) сила удара увеличивается с увеличением жёсткости сооружения.
Пример 15.7. При забивке деревянной сваи d = 0,2 м, длиной l = 6,5 м (рис.15.16) молот копра весом G = 1,6 кН падает с высоты. h = 0,6 м. Определить динамические напряжения в сечениях сваи, условно принимая, что нижнее сечение не смещается. Модуль упругости для древесины вдоль волокон E = 0,1·105 МПа.
Решение.
Площадь поперечного сечения сваи A = πr2 = π·112 = 380,133 см2.
Жёсткость сваи при сжатии EA = 0,1·108·380,133·10-4 = 380133 кН.
Величина продольного статического укорочения сваи
![]() = 27,36·10-6
м.
= 27,36·10-6
м.
Величина динамического коэффициента (15.33)
![]() = 210,43.
= 210,43.
Величина статического напряжения в свае
σG = G/A = 1,6/380,133·10-4 = 42,09 кН/м2.
Величина динамического напряжения
σдин = μσG = 210,43·42,09 = 8857 кН/м2 = 8,857 МПа.
15.3. Колебания упругих систем с несколькими степенями свободы
15.3.1. Свободные колебания
Как отмечалось выше, реальные сооружения обладают распределённой массой и поэтому имеют бесконечное число степеней свободы. При проведении инженерных расчётов распределённые массы, как правило, приводятся к сосредоточенным. Число сосредоточенных масс и, следовательно, число степеней свободы зависит от вида конструкции и от требуемой степени точности расчёта.
Ниже будем рассматривать свободные и вынужденные колебания без учёта диссипативных сил и на основе ранее принятых допущений
Рассмотрим невесомую балку с n сосредоточенными массами (рис.15.17). При принятых допущениях данная система будет иметь n степеней свободы. Если балку вывести из состояния равновесия, она будет совершать свободные колебания. В процессе свободных незатухающих колебаний на массы будут действовать только силы инерции J(t), которые и определяют деформированный вид балки.
Тогда, применяя принцип независимости действия сил, перемещение любой массы mk можно представить как сумму перемещений
yk(t)=δk1J1(t) + δk2J2(t) + ... + δkkJk(t) + ... + δkjJj(t) + δknJn(t), (15.35)
где δkj – коэффициент податливости, т.е. перемещение k-той массы от действия единичной силы, приложенной в точке, где расположена j-тая масса. Выражения (15.35) составляются для каждой массы расчётной схемы при k = 1, 2, ……n.
Входящие в выражение (15.35) инерционные силы, как известно, определяются выражениями
Jj (t)= −mjÿj(t) при j = 1, 2, ……n. (15.36)
Подставив (15.36) в (15.35) и перенеся все члены влево, получим
yk1(t)+ δk1 m1ÿ1(t)+ δk2 m2ÿ2(t) + ...+ δkk mkÿk(t)+ ... + δkn mnÿn(t) = 0 (15.37)
При k = 1, 2, ……n выражения (15.37) представляют собой систему однородных дифференциальных уравнений, описывающих колебания расчётной схемы с n степенями свободы. Для такой системы возможны n частот свободных колебаний, которым будут соответствовать n возможных форм колебаний. Совокупность частот данной системы принято называть спектром частот. В пределах каждой из форм колебаний все точки будут колебаться с частотой ω.
В соответствии с этим для любой k-той массы её перемещение будет иметь вид:
yk(t)=ak sinωt, (15.38)
где ak – амплитуда колебаний k-той массы.
Дважды продифференцируем по времени выражение (15.38):
ÿk(t)= −ω2 ak sinωt.
Подставим выражения перемещений масс y(t) и их вторые производные в систему уравнений (15.37). Нетрудно заметить, что каждое слагаемое в каждом из уравнений системы (15.37) содержит общий множитель sinωt, на который можно сократить все члены этой системы. После сокращения получим
a1δk1 m1ω2+ a2δk2 m2ω2+ ...+ ak(δkk mkω2−1)+ ... + anδkn mnω2 = 0,
или, разделив все члены на ω2,
a1δk1
m1+
a2δk2
m2+
...+ ak(δkk
mk−![]() )+
... + anδkn
mn
=
0.
(15.39)
)+
... + anδkn
mn
=
0.
(15.39)
Выражение (15.39) при k = 1, 2, ……n является системой линейных однородных уравнений относительно амплитуд ak колебаний масс. В эту систему кроме n неизвестных амплитуд входит неизвестная величина 1/ ω2.
Как видно из (15.39), что если массы системы колеблются с одной и той же общей для всех частотой ω, то форма колебаний, определяемая амплитудами масс, не зависит от времени, т.е. для каждого момента отношение перемещений масс к перемещению любой из них является величиной постоянной.
Такие колебания, при которых все точки системы с n степенями свободы колеблются с одинаковой частотой, а форма колебаний при этом не зависит от времени, называются главными колебаниями, а их формы колебаний – главными формами.
Известно, что однородные системы уравнений (без свободных членов) имеют два решения. Одно из них является тривиальным, когда все амплитуды ak =0. Это решение не представляет интереса, так как представляет случай отсутствия колебаний. Отличные от нуля значения амплитуд возможны тогда, когда определитель, составленный из коэффициентов при неизвестных системы уравнений (15.39) равен нулю, т.е.
 (15.40)
(15.40)
Если определитель раскрыть, то получим алгебраическое уравнение n-ой степени относительно параметра 1/ ω2. Уравнение в форме (15.40) или в развёрнутой форме носит название уравнения частот. Впервые оно было получено в астрономии, поэтому в литературе получило название векового уравнения.
Решив (15.40), найдём n значений частот свободных колебаний ω.
Для практических целей часто бывает достаточно определить низшую (наименьшую) частоту свободных колебаний, представляющую наибольшую опасность в смысле возникновения резонанса при действии вибрационной нагрузки. Это объясняется следующим. Во-первых, резонанс на низшей частоте приводит к наибольшему динамическому коэффициенту. Во-вторых, если даже частота возмущающей силы значительно превышает низшую частоту свободных колебаний, то резонанс на этой частоте всё же может возникнуть при разгоне машины при её запуске. Поэтому низшую частоту иногда называют частотой основного тона колебаний. Следующий по порядку тон колебаний называется первым обертоном и т.д.
Определив частоты свободных колебаний, можно для каждой частоты на основании (15.39) определить формы колебаний.
Запишем систему уравнений (15.39) для любой определённой из (15.40) частоты ωj.
 (15.41)
(15.41)
Система уравнений (15.41) может быть превращена в неоднородную, если все её члены разделить на одну из амплитуд или задать ей значение, равное единице, что то же самое. В результате в одном из уравнений системы (15.41) появится свободный член, и, решая систему из (n – 1), мы определим величины других амплитуд по отношению к выбранной. Полученные значения обычно называют относительными амплитудами.
Систему уравнений (15.41) при определении значений относительных амплитуд можно преобразовывать как угодно, что не отразится на соотношениях между амплитудами. Аналогичные математические преобразования можно производить и с уравнением частот (15.40). Один из вариантов этих преобразований покажем в ниже приведённом примере.
Определитель (15.40) можно представить в матричной форме
![]() ,
(15.42)
,
(15.42)
где
![]() – единичная матрица;
– единичная матрица;
![]() –
матрица коэффициентов определителя
(15.40) в действительном или преобразованном
виде; λ – корень векового уравнения,
содержащий величину 1/
ω2.
–
матрица коэффициентов определителя
(15.40) в действительном или преобразованном
виде; λ – корень векового уравнения,
содержащий величину 1/
ω2.
С математической точки зрения решение уравнения (15.42) есть нахождение собственных чисел и собственных векторов матрицы B. Собственные числа представляют собой корни λi векового уравнения, а собственные вектора представляют относительные амплитуды, соответствующие каждому корню.
При правильном решении векового уравнения должны выполняться следующие проверки:
Определитель матрицы должен равняться произведению собственных чисел, т.е. D( ) = ∏ λi.
След матрицы (сумма главных коэффициентов) должен равняться сумме собственных чисел, т.е. Sp =∑bii = ∑ λi.
Пример 15.8. Определить частоты и построить формы свободных колебаний для консольной балки с осью ломаного очертания (рис. 15.18, а).
Решение.
1. Степень свободы масс Wm =2. Две сосредоточенные массы расчётной схемы могут совершать колебания по двум направлениям (рис. 15.18, б).
2. Уравнение частот при Wm =2 для данной расчётной схемы имеет вид
 .
.
3. Для определения коэффициентов уравнения частот последовательно прикладываем единичные силы по направлению колебаний масс (состояния 1 и 2 на рис. 15.18, в и г) и строим эпюры M1 и M2.
Определённые по интегралу Максвелла-Мора коэффициенты уравнения частот имеют следующие значения:
![]() (м/кН);
(м/кН);
![]() (м/кН);
(м/кН);
![]() (м/кН).
(м/кН).
4. Подставляем найденные коэффициенты в уравнение частот и производим его решение.
 .
.
Для начала упростим полученную запись уравнения частот, умножив все его члены на 2EI/9m и введя обозначение λ= 2EI/9mω2.
В результате получим уравнение частот в преобразованном виде:
![]() .
.
Раскрывая определитель, получим квадратное уравнение относительно параметра λ: (8 – λ)(4 – λ) − 3·6 = 0 или λ 2 – 12 λ + 14 = 0, откуда
λ 1 = λmax= 10,69; λ 2 = 1,31.
5. Производим проверки полученного решения.
Матрица коэффициентов уравнения частот имеет вид
![]() .
.
Первая проверка: D( ) = 8·4 – 3·6 = 14;
∏ λi = 10,69·1,31 = 14,0039,
следовательно, D( ) ≈ ∏ λi с погрешностью 0,0028 % , что вполне допустимо.
Вторая проверка: Sp =∑bii = 8 + 4 = 12;
∑ λi = 10,69 + 1,31,
следовательно, Sp =∑ λi.
Определяем частоты свободных колебаний. На основании принятого выше обозначения круговая частота свободных колебаний определяется из выражения
 .
.
Тогда частота основного тона будет
 (с-1),
(с-1),
а частота первого обертона
 (с-1).
(с-1).
Производим построение форм колебаний на основании преобразованной системы уравнений (15.41), которая в данной задаче имеет вид:
(8 – λi)v1i + 6v2i = 0,
3v1i + (4 – λi)v2i = 0,
где v1i и v2i – относительные амплитуды масс при i –той частоте.
Для построения форм колебаний зададим одной из амплитуд значение, равное единице. Тогда вторую амплитуду найдём из любого уравнения приведённой системы.
1 – я форма колебаний. λ 1 = λmax= 10,69.
Рассмотрим первое уравнение системы (8 – λ1)v11 + 6v21 = 0.
При v11 =1 вторая относительная амплитуда v21 = 0,448,
2 – я форма колебаний. λ 2 = 1,31.
Рассмотрим первое уравнение системы (8 – λ2)v12 + 6v22 = 0.
При v12 =1 вторая относительная амплитуда v22 = – 1,116.
Деформированные состояния расчётной схемы, соответствующие формам колебаний, приведены на рис. 15.19 с указанием найденных значений относительных амплитуд.
Пример 15.9. Определить частоты и построить формы свободных колебаний для статически неопределимой рамы с двумя сосредоточенными массами (рис. 15.20, а).
Решение.
1. Степень свободы масс Wm =2. Обе сосредоточенные массы расчётной схемы могут совершать колебания только по вертикали (рис. 15.20, б).
2. Уравнение частот при Wm =2 для данной расчётной схемы имеет вид
 .
.
3. Для определения коэффициентов уравнения частот последовательно прикладываем единичные силы по направлению колебаний масс (состояния 1 и 2 на рис. 15.20, в и г) и строим эпюры M1 и M2.
Так как заданная схема статически неопределима, расчёт по обоим состояниям производим методом перемещений (nк = 1 < nc = 4).
Относительные жёсткости стержней рамы:
стойка i1 = EI/6 = i;
левый ригель i2 = 2EI/8 = 1,5i;
правый ригель i3 = 1,5EI/6 = 1,5i.
Основная система метода перемещений и эпюра от принудительного поворота дополнительный связи на единичный угол показаны на рис. 15.20, д.
Каноническое
уравнение метода
![]() ,
где j
– порядковый номер загружения.
,
где j
– порядковый номер загружения.
Коэффициент при неизвестном, определённый по , r11 = 14,5i.
Расчёт по состоянию 1 (рис.15.20, в).
Эпюра грузового
состояния
показана на рис. 15.20, е,
откуда свободный член канонического
уравнения
![]() = 1 м.
= 1 м.
Из решения
канонического уравнения
![]() = − 1/14,5i.
= − 1/14,5i.
Эпюра изгибающих
моментов состояния 1,
построенная на основании принципа
независимости действия сил как
![]() ,
показана на рис. 15.21, а.
,
показана на рис. 15.21, а.
Расчёт по состоянию 2 (рис.15.20, г).
Эпюра грузового
состояния
![]() показана на рис. 15.20, ж,
откуда свободный член канонического
уравнения
показана на рис. 15.20, ж,
откуда свободный член канонического
уравнения
![]() = −1,125 м.
= −1,125 м.
Из решения
канонического уравнения
![]() = 1,125/14,5i.
= 1,125/14,5i.
Эпюра изгибающих
моментов состояния 2,
построенная на основании принципа
независимости действия сил как
![]() ,
показана на рис. 15.21, б.
,
показана на рис. 15.21, б.
6. При определении коэффициентов уравнения частот воспользуемся правилами определения перемещений в статически неопределимых системах, сформулированными в подразд. 14.5. Выберем для состояний 1 и 2 статически определимые основные системы так, чтобы “перемножение” эпюр было бы как можно проще. Вспомогательные состояния 1 и 2 в статически определимых системах и соответствующие им эпюры и показаны на рис. 15.21, в и г.
Определённые по интегралу Максвелла−Мора коэффициенты уравнения частот имеют следующие значения:
![]() (м/кН);
(м/кН);
![]() (м/кН);
(м/кН);
![]() (м/кН).
(м/кН).
7. Подставляем найденные коэффициенты в уравнение частот и производим его решение.
 .
.
Для начала упростим полученную запись уравнения частот, умножив все его члены на EI/0,466m и введя обозначение λ= EI/0,466mω2.
В результате получим уравнение частот в преобразованном виде:
![]() .
.
Раскрывая определитель, получим квадратное уравнение относительно параметра λ: (13,815 – λ)(3,94 – λ) − 2 = 0 или λ 2 – 17,555 λ + 52,431 = 0, откуда λ 1 = λmax= 14,0135; λ 2 = 3,7415.
8. Производим проверки полученного решения.
Матрица коэффициентов уравнения частот имеет вид
![]() .
.
Первая проверка: D( ) = 13,815·3,94 – 2·1 = 52,4311;
∏ λi = 14,0135·3,7415 = 52,4315.
следовательно, D( ) ≈ ∏ λi с погрешностью 0,003 % , что вполне допустимо.
Вторая проверка: Sp =∑bii = 13,815 + 3,94 = 17,755;
∑ λi = 14,0135 + 3,7415 = 17,755,
следовательно, Sp =∑ λi.
Определяем частоты свободных колебаний. На основании принятого выше обозначения круговая частота свободных колебаний определяется из выражения
 .
.
Тогда частота основного тона будет
 (с-1),
(с-1),
а частота первого обертона
 (с-1).
(с-1).
Производим построение форм колебаний на основании преобразованной системы уравнений (15.41), которая в данной задаче имеет вид:
(13,815 – λi)v1i − v2i = 0,
−3v1i + (3,940 – λi)v2i = 0,
где v1i и v2i – относительные амплитуды масс при i –той частоте.
Для построения форм колебаний зададим одной из амплитуд значение, равное единице. Тогда вторую амплитуду найдём из любого уравнения приведённой системы.
1 – я форма колебаний. λ 1 = λmax= 14,0135.
Рассмотрим первое уравнение системы (13,815 – λ1)v11 − v21 = 0.
При v11 =1 вторая относительная амплитуда v21 = − 0,1985,
2 – я форма колебаний. λ 2 = 3,7415.
Рассмотрим первое уравнение системы (13,815 – λ2)v12 − v22 = 0.
При v12 =1 вторая относительная амплитуда v22 = 10,0735.
Деформированные состояния расчётной схемы, соответствующие формам колебаний, приведены на рис. 15.21, д с указанием найденных значений относительных амплитуд.
15.3.2. Вынужденные колебания при действии вибрационной нагрузки
При действии вибрационной нагрузки на систему с несколькими степенями свободы рассмотрим, как и в подразд. 15.2.2 установившиеся колебания, т.е. изучим стационарный процесс, который наступает после затухания свободных колебаний.
Действующая динамическая нагрузка изменяется по гармоническому закону, т.е. F(t) = Fsinθt; q(t) = qsinθt; M(t) = Msinθt, и может быть приложена в любом месте расчётной схемы.
Усилия и перемещения, полученные в результате динамического расчёта также будут изменяться по этому же закону, т.е.
S(t) = S sinθt; Δ(t) = Δ sinθt, (15.43)
где S и Δ – амплитудные значения усилий и перемещений.
Следовательно, задачей динамического расчёта является нахождение амплитудных значений усилий и перемещений. При необходимости определения усилий и перемещений в любой момент времени, используется зависимость (15.43).
Рассмотрим невесомую балку с n степенями свободы (рис.15.22) и составим для неё выражение перемещений типа (15.35). Но в данном случае к правой части этих выражений добавятся ещё перемещения, вызванные заданной динамической нагрузкой.
На основании принципа независимости действия сил, перемещение любой массы mk можно представить как сумму перемещений
yk(t)=δk1J1(t) + δk2J2(t) + ... + δkkJk(t) + ... + δknJn(t)+ΔkFsinθt. (15.44)
Выражения (15.43) составляются для каждой массы расчётной схемы при k = 1, 2, ……n.
Входящие в выражение (15.44) инерционные силы, как известно, определяются выражениями
Jj (t)= −mjÿj(t) при j = 1, 2, ……n, (15.45)
а перемещения при установившихся колебаниях
yk(t)=ak sinθt, yj(t)=ajsinθt (15.46)
где ak ,aj– амплитуды колебаний k-той и j-той масс.
Дважды продифференцируем по времени выражение (15.46) и подставив его в выражение для инерционных сил (15.45), получим
Jj (t)= −mjÿj(t) = ajmj θ2 sinθt = Jj sinθt. (15.47)
В (15.47) обозначение Jj=ajmjθ2 называют амплитудным значением инерционной силы, зная которую можно определить амплитуду колебаний массы при вынужденных колебаниях
aj = Jj /mjθ2. (15.48)
Учтя (15.48), выразим
перемещения масс k
(k
= 1…n)через
инерционные силы:
![]() (15.49)
(15.49)
Подставим выражения перемещений масс y(t) из (15.49) в левую часть уравнения (15.44), а выражения инерционных сил (15.47) – в правую:
![]() = δk1J1sinθt+
δk2J2sinθt+
...+ δkk
Jksinθt+
...+ δknJnsinθt
+ΔkFsinθt.
= δk1J1sinθt+
δk2J2sinθt+
...+ δkk
Jksinθt+
...+ δknJnsinθt
+ΔkFsinθt.
Полученное выражение сократим на sinθt и приведём к каноническому виду, перенеся все члены в одну сторону:
δk1J1+
δk2J2
+ ...+ (δkk
−![]() )Jk
+ ...+
δknJn
+ ΔkF
= 0,
)Jk
+ ...+
δknJn
+ ΔkF
= 0,
или, введя обозначение
 ,
(15.50)
,
(15.50)
получим
δk1J1+
δk2J2
+ ...+
![]() Jk
+ ...+
δknJn
+ ΔkF
= 0.
(15.51)
Jk
+ ...+
δknJn
+ ΔkF
= 0.
(15.51)
Выражение (15.51) при k = 1, 2, ……n является системой алгебраических уравнений относительно амплитудных значений инерционных сил Jk .
Так как в отличие от задач статики, при динамическом воздействии все перемещения и усилия в расчётной схеме зависят не только от внешней нагрузки, но и от сил инерции, то, определив амплитуды этих сил, на основании принципа независимости действия сил можем определить амплитудные значения искомых усилий:
Sk = Sk1J1+ Sk2J2 + ...+ Skk Jk + ...+ SknJn + ΔkF, (15.52)
где Skj (j = 1, 2, …n)– усилия в заданной расчётной схеме от единичных сил, приложенных по направлению действия сил инерции, SkF – усилия от амплитудного действия внешней динамической нагрузки.
Методика определения динамических усилий и перемещений через амплитудное значение инерционной силы применяется и для систем с одной степенью свободы, когда направления возмущающих нагрузок не совпадают с направлением сосредоточенной массы, и динамический коэффициент определить нельзя.
Пример 15.10. Построить динамическую эпюру изгибающих моментов для консольной балки с двумя сосредоточенными массами, рассмотренной в примере 15.8 (рис. 15.23, а), при действии возмущающей силы F(t) = 120sinθt кН. Круговая частота возмущающей силы θ = 0,7ωmin.
Решение.
1. При sinθt = 1 на расчётную схему будут действовать амплитудные значения возмущающей силы F и инерционных сил J1 и J2 (рис. 15.23, б).
2. Система канонических уравнений для определения амплитудных значений инерционных сил для расчётной схемы с двумя степенями свободы будет иметь вид

3. Из примера 15.8 минимальная частота свободных колебаний
 с-1,
значит
с-1,
значит
 с-1.
с-1.
4. Значения податливостей по направлению колебаний обеих масс также были определены в примере 15.8 по расчетным эпюрам (рис. 15.23, в, г):
![]() (м/кН);
(м/кН);
![]() (м/кН);
(м/кН);
![]() (м/кН).
(м/кН).
Главные коэффициенты при неизвестных системы канонических уравнений определяем по формуле (15.50).
 (м/кН),
(м/кН),
 (м/кН).
(м/кН).
5. Так как направление возмущающей силы F(t) совпадает с направлением J2 (рис. 15.23, б), то эпюра изгибающих моментов MF = M2F (рис. 15.23, д) и, соответственно, свободные члены канонических уравнений будут:
 (м);
(м);
 (м).
(м).
6. Подставляя все найденные значения в систему канонических уравнений и сокращая на общий множитель 1/EI, получим уравнения в численном виде
− 62,224J1 + 13,5J2 + 1620 = 0,
13,5J1 − 40, 112J2 +1080 = 0,
а из их решения J1 = 34,387 кН, J2 = 38,498 кН.
7. Динамическая эпюра, построенная на основании принципа независимости действия сил Mдин = M1 J1 + M2 J2 + MF, показана на рис. 15.24.
Пример 15.11. Построить динамическую эпюру изгибающих моментов для статически неопределимой рамы с двумя сосредоточенными массами, рассмотренной в примере 15.9 (рис. 15.25, а), при действии возмущающих нагрузок F(t) = 6sinθt кН и q(t) = 24sinθt кН/м. Круговая частота возмущающей силы θ = 0,75ωmin.
Решение.
1. При sinθt = 1 на расчётную схему будут действовать амплитудные значения возмущающей силы F и инерционных сил J1 и J2 (рис. 15.25, б).
2. Система канонических уравнений для определения амплитудных значений инерционных сил для расчётной схемы с двумя степенями свободы будет иметь вид
3. Из примера 15.9 минимальная частота свободных колебаний
 с-1,
значит
с-1,
значит
 с-1.
с-1.
4. Значения податливостей по направлению колебаний обеих масс также были определены в примере 15.9:
![]() (м/кН);
(м/кН);
![]() (м/кН);
(м/кН);
![]() (м/кН).
(м/кН).
Главные коэффициенты при неизвестных системы канонических уравнений определяем по формуле (15.50).
 (м/кН),
(м/кН),
 (м/кН).
(м/кН).
5. Производим расчёт грузового состояния от амплитудных значений возмущающих нагрузок (рис. 15.25, в). Основная система метода перемещений и эпюра от принудительного единичного поворота дополнительной связи показаны на рис.15.20, д (см. пример 15.9). Эпюра грузового состояния в основной системе приведена на рис. 15.25, г.
Каноническое уравнение метода перемещений
r11Z1 + R1F = 0, где r11 = 14,5i (кНм/рад), R1F = 42 кНм.
Тогда Z1= − R1F / r11 = − 42/14,5i (рад).
Построив эпюру
![]() (рис. 15.25, д),
на основании принципа независимости
действия сил получим эпюру грузового
состояния
(рис. 15.25, е).
(рис. 15.25, д),
на основании принципа независимости
действия сил получим эпюру грузового
состояния
(рис. 15.25, е).
6. Свободные члены канонических уравнений определяем, используя вспомогательные состояния в статически определимых основных системах (рис. 15.21, в и г, пример 15.9):
 (м);
(м);
 (м).
(м).
7. Подставляя все найденные значения в систему канонических уравнений и сокращая на общий множитель 1/EI, получим уравнения в численном виде
− 5,499 J1 − 0,466 J2 + 49,38 = 0,
− 0,466 J1 − 15,998 J2 − 19,551 = 0,
а из их решения J1 = 9,109 кН, J2 = −1,526 кН.
8. Динамическая эпюра, построенная на основании принципа независимости действия сил Mдин = M1 J1 + M2 J2 + MF, показана на рис. 15.26.
Пример 15.12. Построить динамическую эпюру изгибающих моментов для расчётной схемы с одной степенью свободы (рис. 15.27, а), если возмущающая сила F(t) = 6sinθt кН приложена вне направления колебания массы, а частота вынужденных колебаний θ = 0,8ω.
Решение.
1. При sinθt = 1 на расчётную схему будут действовать амплитудные значения возмущающей силы F и инерционной силы J1, (рис. 15.27, б).
2 Каноническое уравнение для определения амплитудного значения инерционной силы для расчётной схемы с одной степенью свободы будет иметь вид
![]()
3. Заданная система статически определима. Строим эпюру M1 от единичной силы, приложенной по направлению колебания массы (рис.15.27, в), и эпюру MF от действия амплитудного значения возмущающей нагрузки (рис. 15.27, г)
4. Значения податливости по направлению колебания массы:
 (м/кН).
(м/кН).
Определяем частоту свободных колебаний
 (с-1).
(с-1).
6. Частота вынужденных колебаний
 (с-1).
(с-1).
7. Коэффициент при неизвестном канонического уравнения определяем по формуле (15.50).
 (м/кН).
(м/кН).
8. Свободный член канонического уравнения
 (м).
(м).
9. Подставляя найденные значения в каноническое уравнение и сокращая на общий множитель 1/EI, получим уравнение в численном виде
− 25,312 J1 + 405 = 0,
а из его решения J1 = 16 кН.
7. Динамическая эпюра, построенная на основании принципа независимости действия сил Mдин = M1 J1 + MF, показана на рис. 15.27, д.
15.3.3. Учёт симметрии в задачах динамики
В симметричных расчётных схемах с симметрично расположенными одинаковыми массами на основании свойств симметрии возможны упрощения как при определении частот свободных колебаний, так при определении усилий от вибрационной нагрузки.
Для симметричных расчётных схем с симметрично расположенными массами возможно разложение форм колебаний на симметричные и кососимметричные, при которых силы инерции также будут либо симметричные, либо кососимметричные.
Упрощение достигается за счёт разделения уравнения частот (15.41) при наличии осей симметрии на уравнения меньших порядков. Так, если расчётная схема имеет одну ось симметрии, уравнение частот разделяется на два уравнения; если расчётная схема имеет две оси симметрии – на четыре уравнения. При этом сумма порядков уравнений остаётся равной порядку исходного уравнения. Разделения уравнения частот (15.41) можно достичь двумя путями – либо использованием групповых перемещений, либо представлением расчётной схемы в виде её симметричной части.
Рассмотрим расчётную схему с тремя степенями свободы масс (рис.15.28, а), имеющую одну ось симметрии. В этой расчётной схеме три формы колебаний можно представить как две симметричных (рис. 15.28, б и в) и одну кососимметричную (рис. 15.28, г). В этом случае для массы m2, расположенной на оси симметрии (рис. 15.29, а) вспомогательное состояние определяется одной единичной силой (рис. 15.29, б); для симметрично расположенных относительно оси симметрии масс m1 и m3 = m2 величины податливостей определяются от групповых единичных сил (рис. 15.29, в и г). При этом побочные податливости, связывающие симметричные и кососимметричные силы инерции, обращаются в ноль. Это и приводит к распаду уравнения частот на два независимых уравнения, из которых одно позволяет определить частоты симметричных свободных колебаний, а другое – кососимметричных.
Приведённые на рис. 15.28 формы колебаний на основании свойств симметрии (см. подразд. 13.5) позволяют назначить на оси симметрии граничные условия при рассмотрении половины расчётной схемы.
На рис 15.30, а изображена половина расчётной схемы для симметричных колебаний. В силу свойства 1 (см. подразд. 13.5) на оси симметрии должен отсутствовать угол поворота, но сечение способно перемещаться по вертикали. Этим условиям соответствует подвижное в вертикальном направлении защемление. Следовательно, для данной расчётной схемы степень свободы масс будет равна Wm = 2, и уравнение частот будет второго порядка. Так как масса m2 расположена непосредственно на оси симметрии и принадлежит одновременно и правой и левой частям схемы, здесь она учитывается в половину своей величины.
Аналогично, для кососимметричных колебаний (рис. 15.30, б) на оси симметрии должно отсутствовать, на основании свойства 2 (§ 13.5), вертикальное перемещение сечения, но разрешён его свободный поворот. Этим условиям соответствует постановка вертикальной шарнирно подвижной опоры. Следовательно, для полученной расчётной схемы степень свободы Wm = 1, и уравнение частот будет первого порядка. Общее число степеней свободы равно трём, но вместо определителя третьего порядка составляются два определителя – второго и первого. Вычисление этих двух определителей существенно легче и короче, чем вычисление определителя третьего порядка.
При действии вибрационной нагрузки последняя, как и при статических расчётах, раскладывается на симметричную и кососимметричную (рис. 15.31).
Меры защиты от динамических воздействий
Вибрационное воздействие, как наиболее опасное для сооружений, в ряде случаев может привести к отрицательным эффектам, понижающим прочностные и эксплуатационные качества конструкции, причём не только при резонансе. Знакопеременные напряжения в сечениях элементов конструкции, возникающие при действии вибрационных нагрузок, приводят к накоплению повреждений в материале в виде трещин и, в итоге, к разрушению. К не влияющим на состояние конструкции можно отнести лишь колебания с ускорением не более 0,03g.
Кроме этого, вибрационные воздействия могут помешать нормальному функционированию технологического оборудования, расположенного в сооружении, а также на работу многих точных приборов.
Колебания конструкций в зависимости от частоты и амплитуды могут оказывать различное физиологическое воздействие на людей. Критерием чувствительности людей к колебаниям с низкими частотами (от 1 до 10 гц) могут служить ускорения колебаний, а при высоких частотах (свыше 10 гц) – скорости колебаний. Характеристики воздействия на людей гармонических колебаний с амплитудами до 1 мм приведены в табл. 15.3.
Таблица 15.3
Характеристики физиологического воздействия
гармонических колебаний
Характеристики воздействия колебаний на людей |
Для частот от 1 до 10 Гц |
Для частот от 10 до 100 Гц |
Предельное ускорение, мм/с2 |
Предельное ускорение, мм/с2 |
|
Не ощутимы |
10 |
0,16 |
Слабо ощутимы |
40 |
0,24 |
Хорошо ощутимы |
125 |
2,0 |
Сильно ощутимы |
400 |
6,4 |
Вредны при длительном воздействии |
1000 |
16 |
Безусловно вредны |
более 1000 |
более16 |
Допустимую амплитуду a0 динамических перемещений определяют по формулам:
![]() ;
;
![]() ,
,
где v0 и w0 – допускаемые пределы скорости (мм/с2) и ускорения (мм/с2), принимаемые по табл. 15.3; f0 – частота колебаний (Гц).
В качестве допускаемых должны приниматься колебания с характеристиками безвредного воздействия на людей.
Для машин и механизмов, устанавливаемых на фундаментах и перекрытиях зданий, как и для самих строительных конструкций, нормами устанавливаются допустимые значения амплитуд колебаний.
Например, при частоте 4 Гц допустимые амплитуды динамических перемещений будут:
1. в помещениях с вибрационными машинами – 0,25·10-3 м;
2. в помещениях без вибрационных машин – 0,1·10-3 м;
3. в помещениях для работников умственного труда – 0,0354·10-3 м.
При больших частотах рекомендуемые амплитуды будут ещё меньше.
В тех случаях, когда в результате динамических расчётов установлено, что требования прочности, жёсткости или параметры характеристик воздействия на людей и оборудование не удовлетворяются, следует принимать меры защиты от динамических воздействий. Эти меры довольно разнообразны и эффективны при условии правильного выбора их в каждом конкретном случае.
В основу практически всех методов защиты от вибрации положено изменение отношения частот вынужденных и свободных колебаний (θ/ω) в ту или другую сторону с выведением из зоны резонанса, где динамические перемещения наибольшие.
Перечислим основные из существующих мер по защите от вибрации.
1. Целесообразная установка машин.
Путём той или иной расстановки машин, служащих источником колебаний, можно уменьшить или даже избежать резонансных явлений. Например, передвинув такую машину ближе к опоре несущей балки (рис. 15.32, а), можно увеличить частоту свободных колебаний последней. Машины, создающие горизонтальные силы инерции, следует располагать так, чтобы эти силы действовали в направлении большей жёсткости здания (рис. 15.32, б).
2. Изменение массы конструкции.
Устройство дополнительного фундамента под машину позволяет уменьшить частоту свободных колебаний последней (рис.15.33).
3. Изменение жёсткости конструкции.
Увеличение жёсткости конструкции путём увеличения размеров её поперечных сечений, уменьшением пролётов или изменением расчётной схемы путём устройства дополнительных элементов (например, шпренгеля, как показано на рис. 15.34) приводит к повышению частот свободных колебаний и может быть использовано для удаления низшей из этих частот как наиболее опасной.
4. Применение виброизоляции.
Виброизоляция является наиболее простым и часто основным средством защиты от вибрации. Различают активную виброизоляцию, назначением которой является уменьшение динамических сил, передаваемых машиной на несущую конструкцию, и пассивную, при помощи которой изолируют те или иные места работы или приборы от колебаний несущих конструкций. В конструктивном плане активная виброизоляция представляет собой устройство, располагаемое между источником колебаний и несущей конструкцией. Типы этих устройств могут быть самыми различными – от обычных прокладок из дерева или резины до специальных стальных пружин (рис. 15.35).
5. Применение виброгасителей.
Динамический виброгаситель представляет собой дополнительно присоединённую массу (рис. 15.36), упругие связи которой и масса подобраны таким образом, чтобы нейтрализовать своими колебаниями колебания от возмущающей нагрузки.
6. Изменение режима работы машин.
Понижение или повышение числа оборотов ротора машины может привести к такому же эффекту, как и повышение или, соответственно, уменьшение жёсткости конструкции, т.е. к уменьшению динамического коэффициента.
Контрольные вопросы
Какие виды динамических нагрузок вы знаете?
Какие основные законы, сформулированные И. Ньютоном, лежат в основе динамики?
Какие виды колебаний Вы знаете? Дайте их характеристики.
Какие методы описания колебательных процессов используются в динамике?
Сформулируйте принцип Даламбера.
Что называется степенью свободы масс?
Какие допущения при определении степени свободы масс обычно вводятся в инженерных расчетах?
На каких предпосылках и как может быть получено дифференциальное уравнение движения точечной массы с одной степенью свободы?
Дайте характеристику свободным затухающим и незатухающим колебаниям.
Дайте определения основным параметрам свободных колебаний (круговой частоте, технической частоте, амплитуде, периоду) и запишите их выражения.
Что такое коэффициент затухания колебаний?
Почему вибрационная динамическая нагрузка является опасной для сооружений?
Какие колебания называют вынужденными?
Какими параметрами характеризуются вынужденные колебания?
Что называется динамическим коэффициентом?
В каких случаях при определении динамических усилий и перемещений можно использовать динамический коэффициент?
Какое явление в динамике называют резонансом?
Какое явление называется ударом и результатом чего оно является?
Что называется динамическим коэффициентом при ударе?
Как и в каких случаях определяется динамический коэффициент при ударе?
Сформулируйте допущения определения частот свободных колебаний в системах с несколькими степенями свободы. На основании какого принципа строительной механики определяется динамической перемещение любой сосредоточенной массы системы?
Какие колебания упругой системы называются главными?
Что называется главными формами колебаний?
Что называется спектром колебаний?
Как записывается уравнение частот для определения частот свободных колебаний в системах с несколькими степенями свободы?
Что называется амплитудным значением инерционной силы при действии вибрационной нагрузки, и как она определяется?
Какие уравнения необходимо составить для определения амплитудных значений инерционных сил при действии вибрационной нагрузки?
На основании какого принципа строительной механики определяются максимальные динамические усилия и перемещения в системах с несколькими степенями свободы при действии вибрационной нагрузки?
Как при действии вибрационной нагрузки определить динамические усилия и перемещения в любой момент времени?
Какие упрощения расчетов возможны при определении свободных колебаний, динамических усилий и перемещений в симметричных расчетных схемах?
Перечислите основные способы защиты сооружений от вибрациоонных явлений.
Глава 16 основы устойчивости сооружений
16.1. Основные положения
Системы, применяемые в качестве строительных конструкций должны находиться в состоянии устойчивого равновесия. Это означает, что если какие-либо случайные причины выведут систему из состояния равновесия, то после удаления этих причин система должна вернуться в первоначальное положение.
Например, простая балка (рис. 16.1, а), загруженная поперечной нагрузкой, находится в состоянии устойчивого равновесия, так как под действием нагрузки она прогибается во вполне определённом направлении, на точно установленную величину, и, следовательно, принимает единственно возможное положение.
Теперь рассмотрим длинную гибкую стойку (рис. 16.1, б), заделанную одним концом и совершенно свободную на другом, где приложена сжимающая сила. Такая стойка не всегда будет находиться в устойчивом равновесии. При малой величине нагрузки она остаётся прямой и испытывает простое сжатие, но при постепенном увеличении нагрузки наступает момент, когда прямолинейная форма становится неустойчивой, появляется возможность искривления стойки и, притом, в любую из двух сторон в плоскости наименьшей жёсткости. К действующим напряжениям сжатия в сечениях стойки добавляются напряжения от изгиба. Описанный случай называют продольным изгибом, т.е. изгибом, вызванным продольной силой, действующей вдоль оси стержня. В рассмотренном случае мы имеем дело с качественным изменением напряжённо-деформированного состояния центрально сжатого стержня при достижении нагрузки какой-то определённой величины.
Таким образом, при заданной схеме сооружения и заданной схеме нагрузки устойчивость равновесного состояния зависит от величины нагрузки. Для каждой конкретной расчётной схемы можно найти такую нагрузку, при которой первоначальная форма равновесия становится неустойчивой и возможно другое, качественно новое деформированное состояния, тоже являющееся состоянием равновесия.
Например, на рис. 16.2 показаны расчётные схемы кольца, параболической арки и рамы, сечения которых при указанной нагрузке испытывают напряжения центрального сжатия, но при достижении нагрузками величин, обычно называемых критическими, появляется новая форма, изогнутая форма равновесия.
Выход системы из первоначального состояния равновесия называется потерей устойчивости, а нагрузка, при небольшом превышении которой возможно осуществление новой устойчивой формы равновесия, называется критической нагрузкой.
Явление потери устойчивости в строительных конструкциях опасно тем, что изменение напряжённо- деформированного состояния приводит к многократному увеличению напряжений в сечениях элементов расчётной схемы. Кроме того, сам процесс потери устойчивости происходит очень быстро (во многих случаях мгновенно). Оба этих фактора практически приводят разрушению сооружения. В мировой строительной практике известно достаточное число катастроф крупных инженерных сооружений, происшедших в результате потери устойчивости.
Первые исследования потери устойчивости сжатых упругих стержней были выполнены Л. Эйлером (1744 г.).
Построение математической модели задач устойчивости значительно сложнее, чем при решении задач прочности. Поэтому при выборе расчётной схемы для одиночных стержней и рам вводятся дополнительные допущения, практически приводящие все реальные задачи к идеализированным, но позволяющие описать получение решения на основе достаточно простой математической модели:
1. полагают, что расчётная схема образована из идеально прямых стержней;
2. стержни расчётной схемы до момента потери устойчивости испытывают только продольные деформации;
3. в момент потери устойчивости для сплошных стержней учитываются только деформации изгиба, т.е. как и при решении задач прочности, влиянием продольных и поперечных деформаций пренебрегают;
4. предполагается, что критическое состояние конструкции при действии нескольких сжимающих сил достигается путём одновременного их возрастания с сохранением постоянного соотношения между ними;
5. рассматривается потеря устойчивости при бесконечно малых деформациях, что позволяет использовать при решении задач приближённое дифференциальное уравнение изогнутой оси стержня (10.19)
![]() .
.
Общепринятыми и часто встречающимися критериями устойчивости являются статический, энергетический и динамический. В предлагаемом учебнике будет использован только первый критерий, позволяющий решение задач устойчивости консервативных систем. Для таких систем работа, совершаемая внешними силами, не зависит от пути, проделываемого силами при переходе из начального состояния расчётной схемы в конечное (как и при решении задач прочности). Пример консервативных систем показан на рис. 16.1, б и 16.2, когда направление приложенных нагрузок не меняется при потере устойчивости.
При использовании статического критерия устойчивости предполагается следующее. Система после потери устойчивости занимает новое равновесное состояние, качественно отличное от первоначального. Значит, в равновесии находится и любой бесконечно малый элемент этой системы. Записав дифференциальные уравнения равновесия бесконечно малого элемента в деформированном состоянии под действием внутренних и внешних сил и проинтегрировав эти уравнения, можно найти форму потери устойчивости и критическую нагрузку
16.2. Устойчивость центрально сжатых прямолинейных стержней
Постановка задач устойчивости прямолинейных стержней зависит от степени свободы рассматриваемой расчётной схемы. В данном случае под степенью свободы будем понимать число независимых параметров W, полностью определяющих возможные перемещения всех точек расчётной схемы.
Для стержней очень большой жёсткости, когда для упрощения расчёта можно считать EI→∞, их устойчивость определяется податливостью опорных связей, Например, для стойки с упругой опорой, изображённой на рис. 16.3, а, степень свободы W = 1, так как её положение определяется одним параметром – углом поворота α вокруг нижней неподвижной опоры. Для стойки из трёх звеньев (рис. 16.3, б) степень свободы W = 2, так как положение всех трёх звеньев может быть определено при помощи двух параметров – линейных перемещений шарниров А и В.
Для реальных упругих систем (рис. 16.3, в) степень свободы W = ∞, так как, чтобы полностью определить её деформированную схему, необходимо знать перемещения всех точек.
Для расчётных схем, состоящих из стержней большой жёсткости, критическую нагрузку находят, составляя уравнения равновесия для предполагаемой формы потери устойчивости.
Покажем это на конкретных примерах.
Пример 16.1. Определить критическую силу для абсолютно жёсткой стойки (рис. 16.4, а), имеющей одну упругоподатливую опору (пружину) с коэффициентом жёсткости r.
Решение.
Задаём возможную форму потери устойчивости. Стойка имеет одну степень свободы, так как её положение определяется возможным поворотом вокруг шарнирно неподвижной опоры А. Зададим этот поворот (рис. 16.4, б) и обозначим величину смещения точки приложения сжимающей силы через δ.
Для полученной формы потери устойчивости рассмотрим её равновесное состояние (рис. 16.4, в), в котором реакция упругоподатливой опоры R = r δ.
Для указанного равновесного состояния составим уравнение равновесия так, чтобы в него входили известные величины и сила Fcr. Таким уравнением является
∑МА = 0; − Fcr·δ + R·l = − Fcr·δ + r δ ·l = 0, откуда Fcr = rl.
Пример 16.2. . Определить критическую силу и форму потери устойчивости для стойки (рис. 16.5, а), состоящей из трёх абсолютно жёстких звеньев и имеющей две упругоподатливых опоры (пружин) с одинаковыми коэффициентами жёсткости r. Стойка имеет горизонтальную ось симметрии, проходящую через центр звена CD.
Решение.
Задаём возможную форму потери устойчивости. Стойка имеет две степени свободы, так как её положение определяется возможными поворотами звеньев AC и DB вокруг опор А и B соответственно. Зададим эти повороты (рис. 16.5, б) и обозначим величины смещений упругоподатливых опор через δ1 и δ2.
Для выбранной возможной формы потери устойчивости рассмотрим её равновесное состояние (рис. 16.5, в), в котором реакции упругоподатливых опор будут R1 = r δ1 и R2 = r δ2.
Для определения критической силы составим следующие уравнения равновесия:
 Fcr·2δ2
+ R2·l
+ HB·2l
= 0, (а)
Fcr·2δ2
+ R2·l
+ HB·2l
= 0, (а)
![]() Fcr·2δ1
+ R2·2l
+ HB·3l
= 0. (б)
Fcr·2δ1
+ R2·2l
+ HB·3l
= 0. (б)
Выразим через значения реакций упругоподатливых опор из уравнения равновесия ∑МА = 0; HB·5l + R1·l + R2·4l = 0, HB = − 0,2(R1 + 4R2) и подставим в уравнения (а) и (б). После подстановки значений R1 и R2 и несложной группировки относительно заданных перемещений δ1 и δ2, получим
(в) − 0,4rl·δ1
+ (2Fcr
− 0,6 rl)
δ2 = 0,
− 0,4rl·δ1
+ (2Fcr
− 0,6 rl)
δ2 = 0,
(2Fcr − 0,6 rl) δ1− 0,4rl· δ2 = 0.
Полученная система уравнений (в) является однородной и может иметь нулевое решение при δ1= δ2= 0, что соответствует первоначальному равновесному состоянию (рис. 16.5, а). Ненулевое решение она будет иметь, если нулю будет равен определитель, составленный из коэффициентов при неизвестных δ1 и δ2, т.е.

Раскрывая определитель, получим
(0,4rl)2 − (2Fcr − 0,6 rl)2 = 0,
откуда получаем
два значения критической силы:
![]() = 0,1rl
и
= 0,1rl
и
![]() =
0,5rl.
=
0,5rl.
4. Формы потери устойчивости для каждой полученной критической силы определим, подставив их значения в одно из уравнений системы (в).
При = 0,1rl имеем: − 0,4rl·δ1 + (0,2rl − 0,6 rl) δ2 = 0, откуда δ1= −δ2.
При = 0,5rl имеем: − 0,4rl·δ1 + (rl − 0,6 rl) δ2 = 0, откуда δ1= δ2.
Формы потери устойчивости, соответствующие полученным значениям критических сил, показаны на рис. 16.6.
Нетрудно заметить, что в рассмотренной симметричной расчётной схемы мы получили две формы потери устойчивости: симметричную и кососимметричную, причём наиболее опасной является кососимметричная форма, для которой значение критической силы меньше.
Из рассмотренных примеров можно сделать следующий вывод: в расчётных схемах, в которых центральному сжатию подвергаются абсолютно жёсткие стержни, порядок системы уравнений, составленных для определения критических сил, равен числу степеней свободы.
При решении задач с бесконечным числом степеней свободы, интегрируя дифференциальное уравнение изогнутой оси стержня после потери устойчивости, получаем бесконечное множество возможных форм потери устойчивости и соответствующих им критических сил, из совокупности которых для практических целей необходимо знать минимальную.
В литературе данный метод использования статического критерия обычно называют методом непосредственного интегрирования дифференциального уравнения изогнутой оси стержня. Давая совокупность решений, данный метод при принятых допущениях является точным способом расчёта на устойчивость. Преимущество метода состоит в том, что он наиболее чётко выявляет физическую сущность рассматриваемого явления, недостатком – громоздкость получаемых уравнений при исследовании расчётных схем, состоящих из нескольких стержней.
Рассмотрим применение метода непосредственного интегрирования на классической задаче Л.Эйлера – потере устойчивости шарнирно опёртого стержня (рис. 16.7, а). Для этого стержня зададим наиболее простую возможную форму потери устойчивости (рис. 16.7, б) и рассмотрим её равновесное состояние (рис. 16.7, в). Из уравнений равновесия легко показать, что в данной форме равновесия горизонтальные опорные реакции в точках А и В равны нулю. Рассмотрим произвольное сечение стержня с координатами x и y, для которого из равновесия верхней части стержня (рис. 16.7, г) легко определить выражение для изгибающего момента:
M(x) = Fcry.
Подставив полученное выражение изгибающего момента в дифференциальное уравнение (10.19), получим
![]() .
.
Введя обозначение α2= Fcr/EI, представим дифференциальное уравнение в канонической форме
![]() .
.
Решение полученного однородного дифференциального уравнения известно из курса математики и имеет вид:
y(x) = C1cos αx + C2sin αx.
Произвольные постоянные C1 и C2 найдём из граничных условий сжато-изогнутой стойки (рис. 16.7, в):
при x = 0 y = 0, следовательно C1= 0;
при x = l y = 0, следовательно C2 sin αl= 0.
Соблюдение условия C2 sin αl= 0 возможно в двух случаях:
если C2 = 0, то y(x) всегда равно нулю, следовательно, стержень остаётся прямым, что соответствует состоянию до потери устойчивости;
если sin αl= 0, то αl= 0, π, 2π, 3π ….nπ.
Таким образом,
выражение sin
αl=
0 является уравнением
устойчивости для
рассматриваемого стержня, из которого
можно определить критический
параметр
![]() .
Здесь и далее под термином “критический
параметр” будем понимать любую величину,
содержащую значение Fcr.
.
Здесь и далее под термином “критический
параметр” будем понимать любую величину,
содержащую значение Fcr.
Для дальнейших записей расчётных формул введём выражение для критического параметра в виде:
![]() ,
(16.1)
,
(16.1)
откуда
![]() .
(16.2)
.
(16.2)
Из полученных решений уравнения устойчивости нас не интересует решение ν = αl= 0, так как оно соответствует Fcr = 0; из остальных решений нас интересует только то, которое даёт минимальное значение критической силы, т.е. νmin = αl= π. При данном значении критического параметра получаем
![]() .
(16.3)
.
(16.3)
Наименьшее значение критической силы (16.3) для шарнирно опёртого стержня принято называть эйлеровой критической силой.
В практике применяются стойки с различными условиями закрепления. Решения для них находятся аналогично выше изложенному. Значения критических сил и уравнения устойчивости для стержней с различными условиями закрепления концов приведены в табл. 16.1.
Как видно из табл. 16.1, чем жёстче закреплён стержень, тем большую нагрузку до потери устойчивости он может выдержать.
Таблица 16.1
Значения критических параметров для центрально сжатых стержней

Проведём сопоставление формул (16.2) и (16.3) и приведём (16.2) к эйлерову виду (16.3). Для этого произведем следующие преобразования:
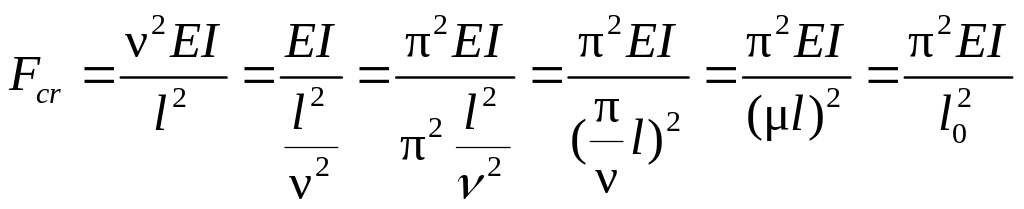 .
.
Таким образом, формулу (16.2) можно представить в виде
 ,
(16.4)
,
(16.4)
где l0 – так называемая приведённая или расчётная длина сжатого стержня. Понятие приведённой длины впервые предложено Ф.С.Ясинским (1856 – 1899):
![]() .
(16.5)
.
(16.5)
Согласно СНиП эта величина, а не критическая сила лежит в основе практических методов расчёта сжатых и сжато-изогнутых стержней элементов конструкций.
Коэффициент μ = π/ν, входящий в (16.5) называют коэффициентом приведения длины центрально сжатого стержня.
Длину l0 можно трактовать как некоторую условную длину шарнирного опёртого по концам стержня, для которого критическая сила равна критической силе для заданного загружения. Из сравнения форм потери устойчивости стержней, приведённых в табл. 16.1 расчётной длине можно дать следующую геометрическую интерпретацию: расчётная длина представляет собой длину полуволны синусоиды, содержащейся в полученной форме потери устойчивости центрально сжатого стержня.
Пример 16.3. Определить критическую силу и расчётную длину центрально сжатой стойки схемы, показанной на рис. 16.8, а.
Решение.
1. Задаёмся возможной формой потери устойчивости расчётной схемы (рис. 16.8, б). В результате изгиба жёсткий узел A повернётся на некоторый угол β. Свободному повороту нижнего сечения стойки препятствует горизонтальный стержень AB, выполняющий по отношению к стойке роль своеобразной упругой пружины. Поэтому расчётная схема стойки может быть представлена в виде вертикального стержня с упругой заделкой в нижнем сечении (рис. 16.8, в).
Определим податливость стержня AB в направлении возможного поворота узла A. Рассмотрим этот стержень отдельно (рис.16.8, г), построим эпюру M1 от единичного безразмерного момента, приложенного по направлению угла поворота и определим податливость
![]() (м/кН).
(м/кН).
Тогда жёсткость круговой пружины определится как величина, обратная податливости r11=1/δ11 = 6EI/l (кН/м).
2. По полученному для стержня равновесному состоянию (рис.16.8, д) определяем изгибающий момент в произвольном сечении с координатами x и y:
M(x) = Fcry − Rx.
3. Подставив полученное выражение изгибающего момента в дифференциальное уравнение (10.19), получим
![]() .
.
Введя обозначение α2= Fcr/EI, представим дифференциальное уравнение в канонической форме
![]() .
(а)
.
(а)
4. Полученное уравнение представляет собой линейное неоднородное дифференциальное уравнение второго порядка. Его решение складывается из двух частей: y(x) = y0 + yч, где y0 – общее решение соответствующего однородного дифференциального уравнения; yч – частное решение уравнения (а), зависящее от его правой части.
Решение однородного уравнения известно из курса математики
y0 = C1cos αx + C2sin αx.
Частное решение уравнения (а) представим в виде полинома первой степени и убедимся, что принятое решение удовлетворяет уравнению (а).
yч = D1x +D2.
Подставим указанное частное решение в уравнение (а):
0 + α2yч = Rx/EI, откуда yч = Rx/ α2EI,
Следовательно, полное решение уравнения (а) будет иметь вид
y(x)= C1cos αx + C2sin αx + Rx/ α2EI, (б)
а его производная y′(x)= − α C1sinαx + α C2 cos αx + R/ α2EI.
5. Уравнение (б) кроме произвольных постоянных C1 и C2 содержит неизвестную величину реакции R. Для их определения используем граничные условия по концам сжато-изогнутого стержня:
при x = 0 y = 0, следовательно, C1= 0;
при x = l y = 0, следовательно, C2sin αl+ Rl/ α2EI = 0;
при x = l y′ = − β, следовательно, α C2 cos αl + R/ α2EI = − β.
Условия 2) и 3) содержат три неизвестных величины: C2, R и β, Для уменьшения числа неизвестных воспользуемся следующим. Как видно из рис. 16.8, д, изгибающий момент M в нижнем сечении стойки можно определить двояко:
− как реакцию в упругой опоре M = β r11 = β 6EI/l;
− как изгибающий
момент в сечении M
=![]() = Rl.
= Rl.
Сравнивая две полученные записи, находим β = Rl2/6EI.
Подставив полученное выражение для угла β в условие 3), введя обозначения критического параметра ν = αl и проведя несложные преобразования, запишем условия 2) и 3) в виде системы уравнений:
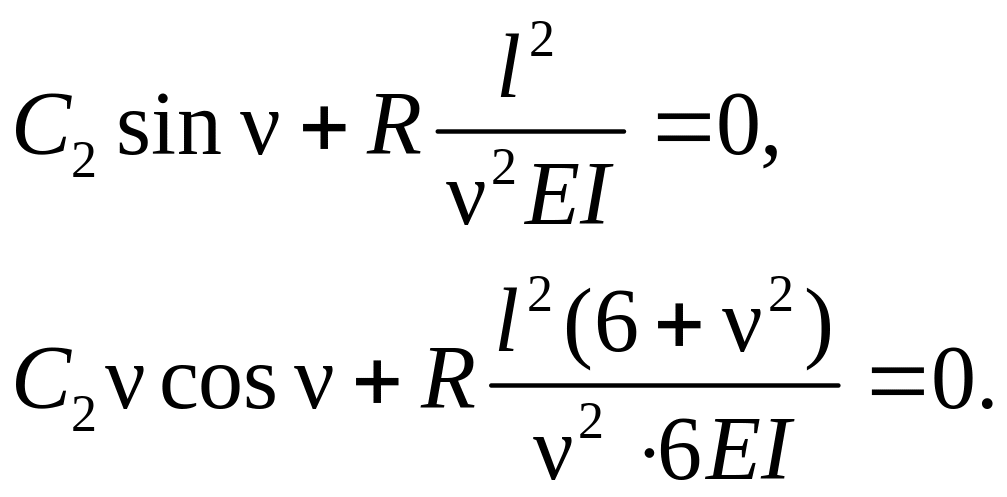 (в)
(в)
6. Полученная система однородных уравнений, как известно, имеет два решения: первое, когда неизвестные C2 = 0 и R= 0, и нас не интересующее; второе, когда C2 ≠ 0 и R ≠ 0. Во втором случае должен равняться нулю определитель, составленный из коэффициентов при неизвестных C2 и R, т.е.:
 ,
,
или после сокращения на l2/ν2EI
 .
(г)
.
(г)
Раскрывая определитель (г), получим уравнение устойчивости относительно критического параметра ν:
 .
(д)
.
(д)
Решение уравнения (д) производится либо специальным программам, либо методом подбора по таблицам специальных функций прил.14. Для осуществления подбора полезно определить границы поиска. Для данной расчётной схемы определяющим при определении границ поиска является угол поворота β.
При потере устойчивости рассматриваемой расчётной схемы возможны два предельных состояния:
β→ 0, что соответствует схеме № 4 табл. 16.1, когда ν = 4,493;
β→∞, что соответствует схеме № 2 табл. 16.1, когда ν = π.
Следовательно, значение критического параметра следует искать в пределах π < ν < 4,493. Искомая величина критического параметра ν= 3,973.
7. Величина критической силы согласно (16.2)
Fcr = 3,9732EI/l2 = 15,785EI/l2.
Расчётная длина стержня согласно (16.5)
l0 = (π/3,973)l = 0,791l.
16.3. Применение метода перемещений при расчёте устойчивости плоских рам
16.3.1. Общие принципы использования метода
Метод перемещений получил широкое распространение при расчёте строительных конструкций. Это объясняется тем, что для большинства расчётных схем, особенно рам, получить кинематически определимую основную систему значительно проще, чем статически определимую. Кроме того, метод перемещений удобен с точки зрения наглядности получения деформированных схем рассчитываемой конструкции. Особенно существенны эти преимущества при расчётах на устойчивость.
Основная система метода перемещений при расчёте на устойчивость получается точно также как и при расчёте на прочность. Но реакции в дополнительных связях определяются уже с учётом продольного изгиба по деформированной схеме.
Согласно принятым допущениям (см. подразд. 16.1) в стержнях рамы, загруженной узловой нагрузкой, вплоть до момента потери устойчивости имеют место только продольные усилия. В этом случае, в силу особенности основной системы метода перемещений, свободные члены системы канонических уравнений равны нулю, и сама система уравнений становится однородной:
r11Z1 + r12Z2 + …+ r1iZi +…+ r1nZn = 0;
r21Z1 + r22Z2 + …+ r2iZi +…+ r2nZn = 0; (16.6)
……………………………………………….
rn1Z1 + rn2Z2 + …+ rniZi +…+ rnnZn = 0.
Однородная система уравнений (16.6) имеет, как известно, два решения:
1. Все неизвестные Zi = 0 (i = 1….n). Это свидетельствует о том, что нагрузка ещё не достигла критического значения, и рама находится в состоянии первоначального устойчивого равновесия.
2. Все неизвестные Zi ≠ 0 (i = 1….n). В этом случае должен равняться нулю определитель, составленный из коэффициентов при неизвестных системы канонических уравнений:
 .
(16.7)
.
(16.7)
Выражение (16.7) является уравнением устойчивости в общем виде на основе метода перемещений. Раскрывая определитель, получим уравнение устойчивости в развёрнутом виде, которое служит для определения критических параметров, через которые выражена критическая нагрузка.
Для определения реакций в дополнительных связях от принудительных единичных смещений связей в основной системе метода перемещений необходимо учесть влияние продольных сил в центрально сжатых стержнях. Эта задача решается методом непосредственного интегрирования дифференциального уравнения изогнутой оси стержня.
Рассмотрим прямолинейный стержень AB (рис.16.9, а), жёстко защемлённый нижним концом и шарнирно опёртым верхним. Определим опорные реакции в этом стержне, вызванные единичным углом поворота его защемления (рис. 16.9, б). Равновесное состояние стержня при таком воздействии показано на рис. 16.9, в.
По полученному для стержня равновесному состоянию определяем изгибающий момент в произвольном сечении с координатами x и y:
M(x) = Fy + Rx.
Подставив полученное выражение изгибающего момента в дифференциальное уравнение (10.19), получим
![]() .
.
Введя обозначение α2= F/EI, представим дифференциальное уравнение в канонической форме
![]() .
(а)
.
(а)
Полученное уравнение представляет собой линейное неоднородное дифференциальное уравнение второго порядка, получение решения для которого было приведено в примере 16.3:
y(x)= C1cos αx + C2sin αx − Rx/ α2EI, (б)
а его производная y′(x)= − α C1sinαx + α C2 cos αx − R/ α2EI.
Уравнение (б) кроме произвольных постоянных C1 и C2 содержит неизвестную величину реакции R. Для их определения используем граничные условия по концам сжато-изогнутого стержня:
при x = 0 y = 0, следовательно, C1= 0;
при x = l y = 0, следовательно, C2sin αl− Rl/ α2EI = 0; (в)
при x = l y′ = − 1, следовательно, α C2 cos αl − R/ α2EI = − 1. (г)
Решая совместно уравнения (в) и (г) относительно R, получим:
 .
(16.8)
.
(16.8)
Выражение (16.8) удобно представить в виде, подобно используемому при решении задач прочности (прил. 10, п. 2). Для этого введём обозначение
 .
(16.9)
.
(16.9)
Тогда
![]() ,
(16.10)
,
(16.10)
а изгибающий момент в защемлении (рис. 16.9, в) будет
M = Rl = 3iφ1(ν). (16.11)
Эпюра изгибающих моментов, соответствующая рассмотренному состоянию стержня, показана на рис. 16.9, г.
В выражениях (16.10) и (16.11) φ1– трансцендентная функция, содержащая критический параметр ν.
Аналогично определяются реакции по концам стержней для других вариантов закреплений и смещений. Все они представлены в таблице прил. 12, а значения соответствующих трансцендентных функций в пределах от 0 до 2π – в табл. прил.13. Для удобства использования всем значениям реакций придан вид, применяемый при решениях задач прочности (см. прил. 10).
Таким образом, определитель (16.7) будет содержать трансцендентные функции (прил. 12), а развёрнутое уравнение устойчивости, полученное после его раскрытия, будет содержать множество корней, из которых необходимым является минимальное ненулевое значение критического параметра ν.
В общем случае параметр ν, определяемый выражением (16.1), зависит от длины стержня l, силы F, действующей на стержень и жёсткости EI, поэтому для различных стержней расчётной схемы он может быть различным. На основании допущения об одновременном возрастании всех нагрузок, дающего соотношения между всеми действующими силами, легко выразить все параметры νi через какой-нибудь один из них. Тогда все коэффициенты rik определителя (16.7) будут функциями только одного параметра.
Например, на раму, изображённую на рис.16.10, имеющую разные длины стержней, разные жёсткости, действуют разные сжимающие силы F1 и F2 , а сила F задана в виде известной величины.
Согласно (16.1) значения критических параметров для стержней 1 и 2 рамы будут следующими
 ;
;
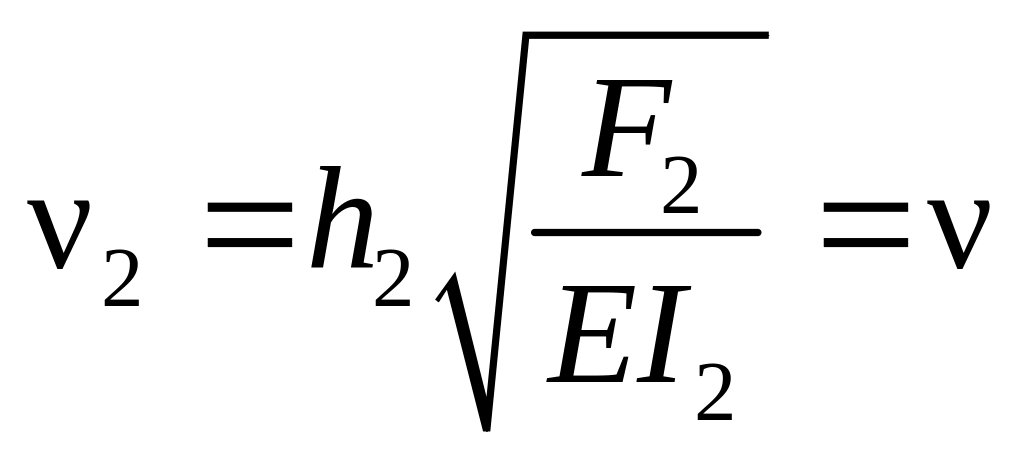 ,
,
где критический параметр для стержня 2 принят в качестве общего множителя. Если обозначить a = h1/h2; b = F1/F2; c = EI1/EI2, то получим, что
 .
.
Учёт силы F с наперёд заданным значением производится введением в расчёт трансцендентных функций, определённых по числовому значению параметра
 .
.
Пример 16.4. Определить критическую силу и расчётную длину центрально сжатого стержня для схемы, показанной на рис. 16.11, а. Эта схема была уже рассмотрена в примере 16.3 при решении задачи методом непосредственного интегрирования.
Относительные жёсткости стержней схемы, приведённые к единому множителю:
стойка i1 = EI/l = i;
ригель i2 = 2EI/l = 2i.
Решение.
1. Расчётная схема имеет один жёсткий узел, закреплённый от горизонтальных и вертикальных смещений. Следовательно, nк = 1.
2. Уравнение устойчивости на основании (16.7) при nк = 1 будет иметь вид r11 = 0.
3. Основная система, полученная введением одной угловой связи, показана на рис. 16. 11, б.
4. Задаём введенной дополнительной связи принудительное единичное смещение (угол поворота), показываем деформированную схему основной системы от этого смещения (рис. 16.11, в) и строим в основной системе эпюру (рис.16.11, г). При этом для ригеля схемы, не испытывающего влияния сжимающих сил, эпюру изгибающих моментов строим по прил. 10, а для сжатой вертикальной стойки – по прил. 12.
5. Реакция в дополнительной связи из условия равновесия
r11 = 3iφ1(ν) + 6i.
6. Подставляя значение r11 в уравнение устойчивости, получаем
φ1(ν) = − 2.
По таблицам прил. 13 находим ν = 3,973. Это значение совпадает с результатом примера 16.3, но само решение методом перемещений значительно проще.
7. Величина критической силы согласно (16.2)
Fcr = 3,9732EI/l2 = 15,785EI/l2.
Расчётная длина стержня согласно (16.5)
l0 = (π/3,973)l = 0,791l.
Пример 16.5. Определить критическую силу и расчётную длину сжатой стойки в раме с абсолютно жёстким ригелем (рис. 16.12, а).
Относительные жёсткости стержней схемы, приведённые к единому множителю:
левая стойка i1 = 2EI/h = 2i;
правая стойка i2 = EI/h = i.
Решение.
1. Рама обладает линейной подвижностью ригеля, узлы которого не способны к повороту. Следовательно, nк = 1.
2. Уравнение устойчивости на основании (16.7) при nк = 1 будет иметь вид r11 = 0.
3. Основная система, полученная введением одной линейной связи, показана на рис. 16. 12, б.
4. Задаём введенной дополнительной связи принудительное единичное смещения, показываем деформированную схему основной системы от этого смещения (рис. 16.12, в) и строим в основной системе эпюру (рис.16.12, г). Для правой стойки схемы, не испытывающей влияние сжимающей силы, эпюру изгибающих моментов строим по прил. 10, а для сжатой левой стойки – по прил. 12.
5. Реакция в дополнительной связи из условия равновесия отсечённого ригеля основной системы (рис.16.12, д)
![]() .
.
6. Подставляя значение r11 в уравнение устойчивости, получаем
η2(ν) = − 0,125.
По табл. прил. 13 находим ν = 3,32.
7. Величина критической силы согласно (16.2)
Fcr = 3,322·2EI/h2 = 22,04EI/h2.
Расчётная длина стержня согласно (16.5)
l0 = (π/3,32)h= 0,946h.
Пример 16.6. Определить критические силы и расчётные длины стоек рамы, приведённой на рис. 16.13, а при следующих данных l = h = 6,0 м, EI = 1500 кНм2.
Относительные жёсткости стержней рамы, приведённые к единому множителю:
левая стойка i1 = 2EI/h = 2i;
средняя стойка i2 = EI/h = i;
правая стойка i3 = 1,5EI/ h = 1,5i;
ригель правого пролёта i4 = EI/h = i.
Решение.
1. Рама имеет один жёсткий узел, способный к повороту при деформации рамы, и её ригель может перемещаться по горизонтали. Следовательно, степень кинематической неопределимости рамы nк = 2.
2. Уравнение устойчивости для рамы на основании (16.7) при nк = 2 будет иметь вид
 .
.
3. Основная система, полученная введением одной угловой и одной линейной дополнительных связей, показана на рис. 16.13, б.
4. Устанавливаем соотношения между критическими параметрами сжатых стоек рамы.
 ;
;
 ;
;

5. Последовательно задаём введенным дополнительным связям принудительные единичные смещения, показываем деформированные схемы основной системы от этих смещений (рис. 16.13, в и г) и строим в основной системе эпюры и : для ригеля − по прил. 10, а для стоек − по прил. 12
6. Определяем реакции в дополнительных связях от единичных смещений:
![]() (рис. 16.13, д);
(рис. 16.13, д);
![]() (рис. 16.13, е);
(рис. 16.13, е);
![]() (рис. 16.13, ж).
(рис. 16.13, ж).
7. Подставим полученные значения коэффициентов при неизвестных в уравнение устойчивости. Учтём, что η2(1,8) = 0,6749 (см. прил.13). Произведя сокращение на 3i/h2 и простейшие алгебраические преобразования, получим уравнение устойчивости в развёрнутом виде:
[1 + 2φ2(1,2ν)]·[8·0,6749 + η1(ν) + 6η2(1,2ν)] – [3φ4(1,2ν)]2 = 0.
Решая полученное уравнение устойчивости методом подбора по табл. прил. 13, находим минимальное значение параметра ν = 2,73.
Величины критических сил (16.2) и расчётных длин (16.5) для сжатых стержней рамы:
средняя стойка рамы
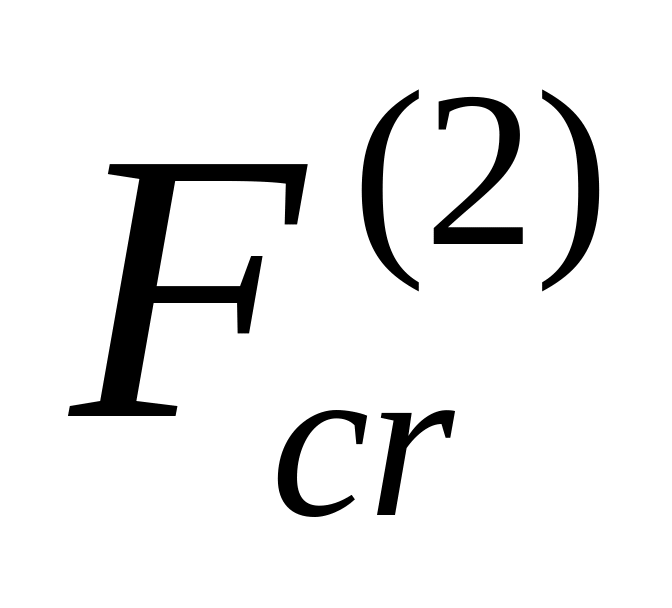 = 2,732·1500/62
= 310,54 кН;
= 2,732·1500/62
= 310,54 кН;
l02 = π·6/2,73 = 6,9 м.
правая стойка рамы
 = (1,2·2,73)2·1,5·1500/62
= 670,76 кН;
= (1,2·2,73)2·1,5·1500/62
= 670,76 кН;
l03 = π·6/(1,2·2,73) = 5,75 м.
9. Проверяем сохранность соотношения между полученными значениями критических сил
/ = 670,76/310,54 = 2,16.
16.3.2. Упрощения при расчёте рам на устойчивость
Для целого ряда расчётных схем использование метода перемещений в расчётах на устойчивость в общем виде является нецелесообразным из-за сложности получаемых уравнений устойчивости. Поэтому, как и при решении задач прочности используются те же приёмы упрощения решений.
Таковыми являются использование основной системы метода перемещений без постановки линейных связей и упрощения, связанные с учётом симметрии.
О с н о в н а я с и с т е м а б е з п о с т а н о в к и л и н е й н ы х
с в я з е й.
Такая основная система может быть использована для расчётных схем типа консольной стойки ступенчатого сечения (рис. 16.14, а), когда ничто не препятствует горизонтальному смещению узлов, за которые принимаются места ступенчатого изменения сечений, а поперечные силы во всех сжатых стержнях равны нулю. К указанному типу расчётных схем можно отнести раму (рис. 16. 14, б) и статически определимую балку ломаного очертания (рис. 16.14, в).
В приведённых расчётных схемах основную систему получают введением только узловых дополнительных связей (“плавающих” заделок), препятствующих только угловым смещениям.
Как и при расчёте на прочность, будем иметь дело с двумя дополнительными типами стержней, которые были показаны в подразд. 14.3.1 (см. рис. 14.13), но в расчётах на устойчивость они загружены сжимающими силами.
Для того, чтобы воспользоваться основной системой без постановки линейных связей, необходимо знать значения реакций для указанных двух типов стержней. Получение этих реакций производится на основе метода непосредственного интегрирования дифференциального уравнения изогнутой оси стержня.
Рассмотрим консольный стержень (рис. 16.15, а), который по своей работе равнозначен стержню, изображённому на рис. 14.13, б, и зададим единичный угол поворота защемления (рис. 16.15, б).
По полученному для стержня равновесному состоянию (рис. 16.15, в) определяем изгибающий момент в произвольном сечении с координатами x и y: M(x) = Fy.
Подставив полученное выражение изгибающего момента в дифференциальное уравнение (10.19), получим
![]() .
.
Введя обозначение α2= Fкр/EI, представим дифференциальное уравнение в канонической форме
.
Мы получили уже знакомое дифференциальное уравнение, решение которого известно: y(x)= C1cos αx + C2 sinαx,
Его производная y′(x)= − α C1sinαx + α C2 cos αx.
Записав граничные условия для рассматриваемого стержня, получим:
при x = 0 y = 0, следовательно, C1= 0;
при x = l y′ = 1, следовательно, α C2 cos αl = 1,
откуда C2 = 1/ α cos αl = l/ν cos ν.
Определив C2, можем записать уравнение изогнутой оси стержня
y(x)= l·sinαx/ν cos ν,
на основании которого определим относительное смещение концов стержня δ = y(l)= l·sinαl/ν cos ν = νl·tg ν.
Изгибающий момент в заделке при F= ν2EI/l2 (16.2) будет (рис. 16.15, г):
M = F δ = iν ·tg ν.
Аналогично получают значения реакций и для второго типа стержня. Выражения для реакций приведены в прил. 12 (п.п. 5 и 6), а значения специальных функций, входящих в эти выражения – в прил. 14.
У ч ё т с и м м е т р и и
Рассмотрим симметричную и симметрично загруженную раму (рис. 16. 16, а). Данная рама является трижды кинематически неопределимой, и при получении основной системы метода перемещений необходимо ввести три дополнительных связи – две угловых и одну линейную. В силу симметрии расчётной схемы можно воспользоваться способом группировки неизвестных для симметрично расположенных неизвестных. Соответственно, рассмотрим три вспомогательных состояния от принудительного смещения связей:
1. симметричный групповой поворот угловых связей (состояние 1, рис. 16.16, б), вызывающий симметричную форму деформации основной системы;
2. кососимметричный групповой поворот угловых связей (состояние 2, рис. 16.16, в), вызывающий кососимметричную форму деформации основной системы;
3. линейное смещение (состояние 3, рис. 16.16, г), также вызывающее кососимметричную форму деформации основной системы.
В силу симметрии побочные коэффициенты r12 = r21 = r13 = r31 = 0, в результате чего общий определитель (16.7) при nк = 3 распадается на два определителя:
 ,
,
что позволяет
рассматривать отдельно
![]() и
и
![]() .
.
Таким образом, при определении устойчивости симметричных и симметрично загруженных рам упрощение расчёта сводится к отдельному рассмотрению симметричной и кососимметричной форм потери устойчивости.
Рассмотрим формы потери устойчивости (рис.16.17, а) для имеющих одинаковые геометрические размеры несвободной (не имеющей горизонтальных смещений ригеля) и свободной (ригель имеет горизонтальные смещения) рам. Нетрудно заметить, что симметричная форма потери устойчивости у этих рам (рис. 16.17, б) одинакова, а кососимметричные формы (рис.16.17, в) разнятся, и существенно.
Приведённые формы потери устойчивости позволяют сделать выводы, и это доказано инженерной практикой, что:
1. для несвободных
рам
![]() <
<
![]() ;
;
2. для свободных рам < .
Также, как и при решении задач прочности, расчётную схему при выбранной форме потери устойчивости можно представит в виде её симметричной части.
На рис. 16.18 рассмотрена симметричная несвободная рама и расчётные схемы для обеих форм потери устойчивости. Степень кинематической неопределимости рамы nк = 2. Для симметричной формы потери устойчивости (рис. 16.18, а) имеем nк = 1, для кососимметричной формы (рис. 16.18, б) – также nк = 1.
По аналогии для свободной рамы при nк = 3 имеем: для симметричной формы потери устойчивости (рис. 16.19, а) – nк = 1; для кососимметричной формы (рис. 16.19, б) – nк = 1. Общее число уравнений меньше трёх, так как при рассмотрении кососимметричной формы возможно использование основной системы без постановки линейной связи.
Пример 16.7. Определить наименьшее значение критической силы для симметричной расчётной схемы, показанной на рис. 16.20, а.
Относительные жёсткости стержней схемы, приведённые к единому множителю:
стойки i1 = EI/l = i;
ригель i2 = 2EI/l = 2i.
Решение.
1. Расчётная схема имеет несмещаемый по горизонтали ригель, следовательно, наименьшей будет критическая сила при симметричной форме потери устойчивости (рис. 16.20, б).
2.Представляем расчётную схему в виде её симметричной части, которая имеет один жёсткий узел, закреплённый от горизонтальных и вертикальных смещений (рис.16.20, в). Следовательно, nк = 1.
3. Уравнение устойчивости на основании (16.7) при nк = 1 будет иметь вид r11 = 0.
4. Основная система, полученная введением одной угловой связи, показана на рис. 16. 20, г.
5. Задаём введенной дополнительной связи принудительное единичное смещения (угол поворота), показываем деформированную схему основной системы от этого смещения (рис. 16.20, д ) и строим в основной системе эпюру (рис.16.20, е). При этом для ригеля схемы, не испытывающего влияния сжимающих сил, эпюру изгибающих моментов строим по прил. 10, а для сжатой вертикальной стойки – по прил. 12.
6. Реакция в дополнительной связи из условия равновесия
r11 = − iνtgν + 4i.
7. Подставляя значение r11 в уравнение устойчивости, получаем
νtgν = 4.
По таблицам прил. 14 находим ν = 1,26.
8. Величина критической силы согласно (16.2)
Fcr = 1,262EI/l2 = 1,59EI/l2.
Расчётная длина стержня согласно (16.5)
l0 = (π/1,26)l = 2,49l.
Пример 16.8. Определить критическую силу и расчётные длины сжатых стоек для симметричной рамы (рис. 16.21, а). Рама имеет один абсолютно жёсткий ригель. Для всех остальных стержней EI – const.
Для сжатых стоек рамы при одинаковых длинах, жёсткости и сжимающей силе величина критического параметра ν − const.
Решение.
1. Ригели рамы способны смещаться по горизонтали, т.е. рама является свободной. Следовательно, наименьшей будет критическая сила при кососимметричной форме потери устойчивости (рис. 16.21, б).
2. Представляем расчётную схему в виде её симметричной части (рис.16.21, в), которая имеет один жёсткий узел, способный к повороту. Поперечные силы в сжимаемых стойках равны нулю, поэтому для полученной схемы можно использовать основную систему без постановки линейных связей. Следовательно, nк = 1.
3. Уравнение устойчивости на основании (16.7) при nк = 1 будет иметь вид r11 = 0.
4. Основная система, полученная введением одной угловой связи, показана на рис. 16. 21, г.
5. Задаём введенной дополнительной связи принудительное единичное смещение (угол поворота), показываем деформированную схему основной системы от этого смещения (рис. 16.21, д ) и строим в основной системе эпюру (рис.16.21, е). При этом для ригеля схемы, не испытывающего влияния сжимающих сил, эпюру изгибающих моментов строим по прил. 10, а для сжатой вертикальной стойки – по прил. 12.
6. Реакция в дополнительной связи из условия равновесия
r11 = 2iν/tgν + 6i.
7. Подставляя значение r11 в уравнение устойчивости, получаем
ν/tgν = − 3.
По таблицам прил. 14 находим ν = 2,45.
8. Величина критической силы согласно (16.2)
Fcr = 2,452EI/l2 = 6,00EI/l2.
Расчётная длина стержня согласно (16.5)
l0 = (π/2,45)l = 1,28l.
16.4. Критические напряжения и пределы применимости формулы Эйлера
Изложенное выше исследование устойчивости сжатого стержня производилось в предположении упругих деформаций. Поэтому и полученные формулы для критической силы тоже справедливы лишь при этом предположении. Назовём критическим сжимающим напряжением σcr напряжение, возникающее в стержне при приложении к нему критической силы (16.4)
 ,
(16.12)
,
(16.12)
где
![]() – радиус инерции поперечного сечения
стержня (8.21);
– радиус инерции поперечного сечения
стержня (8.21);
λ = l0/i – гибкость стержня.
Очевидно, что формула (16.12) справедлива лишь в случае, когда критическое напряжение σcr не превышает предела пропорциональности σpr, т.е.
![]() .
(16.13)
.
(16.13)
Зная модули упругости E и значения σpr, можно по условию (16.13) вычислить предельные значения гибкости для различных материалов и само условие записать в виде
 .
(16.14)
.
(16.14)
Примерные значения предельной гибкости для некоторых материалов приведены в табл. 16.2.
Итак, при λ >λcr для определения критических напряжений и, следовательно, и критических сил можно пользоваться формулой Эйлера, если же λ < λcr, то формула Эйлера становится неприемлемой, а критические напряжения определяются по эмпирической формуле Ф.С.Ясинского, полученной на основе изучения опытных данных:
Таблица 16.2
Значения предельных гибкостей
Материал |
λcr |
Малоуглеродистая сталь Чугун Хромомолибденовая сталь Дюралюминий Древесина (сосна) |
≈100 ≈80 ≈60 51 ≈61 |
σcr = a – bλ +λ2 , (16.15)
где a, b и c – экспериментально определяемые коэффициенты, зависящие от материала (табл. 16.3).
Таблица 16.3
Материал |
Коэффициенты, МПа |
||
а |
b |
c |
|
Малоуглеродистая сталь Чугун Хромомолибденовая сталь Дюралюминий Древесина (сосна) |
310 761 1000 380 40 |
1,14 11,77 5,4 2,185 0,203 |
0 0,052 0 0 0 |
При λ < 40, когда сжимаемые стержни достаточно коротки, разрушение стержня происходит вследствие разрушения самого материала, и расчёт производят на прочность без учёта опасности продольного изгиба.
16.5. Практические расчёты на продольный изгиб
При расчёте сжатых стержней на прочность требовалось выполнение условия (5.23)
![]() .
.
При расчёте же на устойчивость необходимо выполнение условия
![]() ,
(16.16)
,
(16.16)
где A – полная площадь поперечного сечения A (брутто) без учёта местных ослаблений, так как они не оказывают заметного влияния на величину критических напряжений;
ky – коэффициент запаса на устойчивость, зависящий от возможности случайного увеличения сжимающей силы и возможности её внецентренного приложения, от наличия начальных несовершенств в геометрии стержня и способах его закрепления и т.д.
Сопоставим между собой неравенства (5.23) и (15.16) и запишем отношения их правых частей:
![]() ,
откуда
,
откуда
![]() .
(16.17)
.
(16.17)
Величина φ называется коэффициентом продольного изгиба, который определяет степень снижения расчётного сопротивления материала при продольном изгибе. Так как коэффициент продольного изгиба φ зависит от величины критического напряжения (16.12), то очевидно, что он зависит от гибкости стержня и упругих свойств материала. Значения коэффициента φ для различных материалов (прил. 15) устанавливается нормами.
Подставив (16.17) в (16.16), получим
![]() .
(16.18)
.
(16.18)
Практические задачи на продольный изгиб можно на основании (16.18) разделить на три основные типа:
1. Проверка сжатых стержней на устойчивость по формуле (16.18).
2. Определение несущей способности (а по ней - допускаемой нагрузки) при заданных геометрических размерах стержня и виде материала
N ≤ φARγc. (16.19)
3. Определение (подбор) сечения стержня по заданной расчётной схеме, виду материала и величине нагрузки
![]() .
(16.20)
.
(16.20)
Последний тип задач является наиболее сложным. Это объясняется тем, коэффициент φ зависит от гибкости стержня, а гибкость неизвестна, так как неизвестны размеры сечения. Поэтому данную задачу решают методом последовательных попыток, задаваясь вначале значением коэффициента продольного изгиба φ, соответствующего предельному значению гибкости λcr.
Пример 16.9. Определить критическую нагрузку для шарнирно опёртого стального стержня сечением 40 х 60 мм. Длина стержня l = 0,8 м.
Решение.
1. Расчётная длина стержня (см.табл. 16.1, п.2) l0 = l = 0,8 м.
2. Минимальный момент инерции Imin= 6·43/12 = 32 см4.
3. Площадь сечения A = 4·6 = 24 см2.
4. Минимальный
радиус инерции imin=![]() =
1,155 см.
=
1,155 см.
5. Гибкость стержня λ = l0/ imin= 80/1,155 = 69,3 < λcr = 100 (см. табл. 16.2).
6. Значение критического напряжения (16.15) при a = 310 МПа, b = 1.14 МПа, с = 0 (см. табл. 16.3)
σcr = 310 – 1,14·69,3 = 231 МПа.
7. Величина критической силы
Fcr = σcr A = 231·103·24·10-4 = 554,4 кН.
Пример 16.10. Определить критическое напряжение в стальном стержне, один конец которого жёстко защемлён, а другой шарнирно опёрт. Сечение стержня – трубчатое с наружным диаметром D = 60 мм и внутренним d = 50 мм. Длина стержня l = 4 м. Модуль упругости материала E = 2,06·105 МПа.
Решение.
1. Расчётная длина стержня (см. табл. 16.1, п.4) l0 =0,7 l = 2,8 м.
2. Момент инерции I = π(64−54)/64 = 32,938 см4.
3. Площадь сечения A = π(62−52)/4 = 8,639 см2.
4. Жёсткость сечения EI = 2,06·108·32,938·10-8 = 67,852 кН·м2.
5. Радиус инерции
i=![]() =
1,953 см.
=
1,953 см.
6. Гибкость стержня λ = l0/i= 280/1,953 = 143,37 > λcr = 100 (см. табл. 16.2).
7. Величина критической силы (16.4)
Fcr
= π2
EI/![]() =
π2·67,852/2,82
= 85,42 кН.
=
π2·67,852/2,82
= 85,42 кН.
8. Значение критического напряжения
σcr = Fcr /A = 85,42·10-3/8,639·10-4 = 98,88 МПа.
Пример 16.11. Подобрать сечения верхнего пояса (по наибольшему усилию) и раскоса второй панели фермы (рис. 16.22, а). Тип требуемых сечений показан на рис. 16.22, б. Марка стали С255 (Ry = 240 МПа). Коэффициент условия работы γс = 0,95. Величина узловой нагрузки F = 60 кН.
Определить коэффициенты запаса устойчивости принятых сечений из сравнения величин критических сил и сил, которые могут воспринять сечения.
Согласно СНиП II – 23 – 81* расчётные длины элементов плоских ферм при направлении продольного изгиба в плоскости фермы следует принимать:
для поясов, опорных раскосов и опорных стоек l0 = l;
для элементов решётки l0 = 0,8l.
Решение.
1. Определяем усилия в требуемых стержнях фермы.
1.1. В силу симметричности схемы фермы и приложенной к ней нагрузки (рис. 16.22, в) вертикальные опорные реакции будут одинаковыми, т.е.
VA = VB = 0,5∑F = 0,5·7·60 = 210 кН.
1.2. Поскольку ферма является балочной, наибольшие усилия верхнего пояса будут в стержнях четвёртой и пятой панелях фермы. Наибольшее сжимающее усилие определяем из равновесия левой отсечённой части фермы (рис. 16.22, г) по сечению I – I.
∑Mk = 210·9 – 60(6 + 3) + N1·4 = 0; N1 = − 337,5 кН.
1.3. Усилие в раскосе второй панели определяем из равновесия левой отсечённой части фермы (рис. 16.22, д) по сечению II – II.
∑Y = 210 – 60 + N2·cos α = 0; N2 = − 150/0,8 = − 187,5 кН.
2. Подбор сечения верхнего пояса
2.1. Расчётная длина панели l0 = l = 3 м.
2.2. Первое приближение.
Задаёмся коэффициентом продольного изгиба φ1 = 0,25 (при гибкости λ ≈ 170 > λcr =100).
Требуемая площадь одного уголка согласно (16.20)
A1 ≥ 0,5·337,5/(0,25·0,95·240·103) = 29,6·10-4 м2 =29,6 см2.
По сортаменту неравнополочных уголков (см. прил. 8) определяем номер уголка, площадь которого близка к полученной. Таковым является уголок № 16/10 – 160 х 100 х 12 ( А = 30 см2, imin = iz = 2,82 см).
Так как поперечное сечение имеет вертикальную ось симметрии (ось y), минимальный радиус инерции всего сечения будет таким же, как и для одного уголка.
Гибкость принятого сечения
λ = 300/2,82 = 106,4,
а коэффициент продольного изгиба, соответствующий полученной гибкости (прил. 15) φ = 0,501.
Производим проверку принятого сечения по формуле (16.18)
σ = 337,5·10-3/(0,501·2·30·10-4) = 112,28 МПа < Ryγc = 228 МПа.
Как показывает полученный результат, сечение обладает вдвое большим запасом прочности, чем необходимо. Площадь сечения необходимо уменьшить.
2.3. Второе приближение.
Задаёмся коэффициентом продольного изгиба
φ2 = 0,5(φ1+ φ) = 0,5(0,25 + 0,501) ≈ 0,375.
Требуемая площадь одного уголка согласно (16.20)
A2 ≥ 0,5·337,5/(0,375·0,95·240·103) = 19,7·10-4 м2 =19,7 см2.
По сортаменту неравнополочных уголков (прил. 8) принимаем
№ 12,5/8 – 125 х 80 х 10 ( А = 19,7 см2, imin = iz = 2,26 см).
Гибкость принятого сечения
λ = 300/2,26 = 132,7,
а коэффициент продольного изгиба, соответствующий полученной гибкости (прил. 15) φ = 0,351.
Производим проверку принятого сечения по формуле (16.18)
σ = 337,5·10-3/(0,351·2·19,7·10-4) = 244,04 МПа > Ryγc = 228 МПа.
Как видно из последнего полученного результата, необходимо немного увеличить площадь сечения, либо уменьшить гибкость, даже за счёт уменьшения площади сечения
2.4. Третье приближение.
По сортаменту неравнополочных уголков (см. прил. 8) принимаем
№ 14/9 – 140 х 90 х 8 (А = 18 см2, imin = iz = 2,58 см).
Гибкость принятого сечения
λ = 300/2,58 = 116,3,
а коэффициент продольного изгиба, соответствующий полученной гибкости (см. прил. 15) φ = 0,441.
Производим проверку принятого сечения по формуле (16.18)
σ = 337,5·10-3/(0,441·2·18·10-4) = 212,6 МПа < Ryγc = 228 МПа.
Окончательно принимаем сечение верхнего пояса из двух неравнополочных уголков № 14/9 – 140 х 90 х 8 (А = 18·2 = 36 см2), так как недонапряжение принятого сечения составляет 6,75%.
3. Подбор сечения раскоса.
3.1. Расчётная длина панели l0 =0,8 l = 0,8·5 = 4 м.
3.2. Первое приближение.
Задаёмся коэффициентом продольного изгиба φ1 = 0,25 (при гибкости λ ≈ 170 > λcr =100).
Требуемая площадь одного уголка согласно (16.20)
A1 ≥ 0,5·187,5/(0,25·0,95·240·103) = 16,45·10-4 м2 =16,45 см2.
По сортаменту равнополочных уголков (прил. 9) принимаем
№ 10 – 100 х 100 х 8 ( А = 15,6 см2, iz = 3,07 см).
Гибкость принятого сечения
λ = 400/3,07 = 130,3,
а коэффициент продольного изгиба, соответствующий полученной гибкости (см. прил. 15) φ = 0,362.
Производим проверку принятого сечения по формуле (16.18)
σ = 187,5·10-3/(0,362·2·15,6·10-4) = 166 МПа < Ryγc = 228 МПа.
Как показывает полученный результат, сечение обладает почти полуторным запасом прочности. Площадь сечения необходимо уменьшить.
3.3. Второе приближение.
Задаёмся коэффициентом продольного изгиба
φ2 = 0,5(φ1+ φ) = 0,5(0,25 + 0,362) = 0,306.
Требуемая площадь одного уголка согласно (16.20)
A2 ≥ 0,5·187,5/(0,306·0,95·240·103) = 13,44·10-4 м2 =13,44 см2.
По сортаменту равнополочных уголков (прил. 9) принимаем уголок № 9 – 90 х 90 х 8 (А = 13,9 см2, iz = 2,76 см).
Гибкость принятого сечения
λ = 400/2,76 = 144,9,
а коэффициент продольного изгиба, соответствующий полученной гибкости (см. прил. 15) φ = 0,296.
Производим проверку принятого сечения по формуле (16.18)
σ = 187,5·10-3/(0,296·2·13,9·10-4) = 227,86 МПа ≈ Ryγc = 228 МПа.
Окончательно принимаем сечение верхнего пояса из двух равнополочных уголков № 9 – 90 х 90 х 8 (А = 13,9·2 = 27,8 см2).
4. Определяем несущую способность стержней по формуле (16.19):
верхний пояс (А = 36 см2, φ = 0,441)
[N1] = 0,441·36·10-4·0,95·240·103 = 361,97 кН > N1 = 337,5 кН;
раскос (А = 27,8 см2, φ = 0,296)
[N2] = 0,296·27,8·10-4·0,95·240·103 = 187,62 кН > N2 = 187,5 кН;
5. Критические силы стержней с принятыми размерами сечений (16.4)
верхний пояс (Iz= 2·120 = 240 см4; EIz = 2,06·108·240·10-8= 494,4 кН·м2)
![]() = π2·494,4/32
=
542,17
кН;
= π2·494,4/32
=
542,17
кН;
раскос (Iz= 2·106 = 212 см4; EIz = 2,06·108·212·10-8= 436,72 кН·м2)
![]() = π2·436,72/42
= 269,39 кН.
= π2·436,72/42
= 269,39 кН.
6. Коэффициенты запаса устойчивости
для верхнего пояса k1у = /[N1] = 542,17/337,5 = 1,31;
для раскоса k2у = /[N2] = 269,39/187,5 = 1,44.
Пример 16.12. Для рамы, рассмотренной в примере 16.4 (см. рис.16.11, а), подобрать сечение сжатой стойки при F = 180 кН, l = 4 м. Материал стойки – сосна (Rс = 14 МПа). Сечение стойки принять прямоугольным с соотношением сторон h/b =1,5. Продольный изгиб стойки возможен параллельно большей стороне сечения. Коэффициент условия работы γс = 1.
Решение.
1. Расчётная длина стойки (см. пример 16.4, п.7)
l0 = 0,791l = 0,791·4 = 3,16 м.
2. Задаёмся коэффициентом продольного изгиба (см. прил. 15) при гибкости λ = 70 > λcr =61 (см. табл. 16.2).
φ1 =1 – 0,8 (70/100)2 = 0,608.
3. Требуемая площадь сечения (16.20)
A1 ≥ 180/(0,608·14·103) = 211,5·10-4 м2 =211,5 см2.
При A = b·h = 1,5b2 требуемая ширина сечения
![]() = 11,87 см.
= 11,87 см.
Принимаем b = 12 см, h = 1,5b = 18 см.
4. Геометрические характеристики принятого сечения.
A = b·h = 12·18 = 216 см2; Iz = bh3/12 = 12·183/12 = 5832 см4;
![]() = 5,2 см.
= 5,2 см.
5. Гибкость стержня
λ = l0 /iz = 316/5,2 = 60,77 < λcr =61,
а соответствующий ей коэффициент продольного изгиба
φ =1 – 0,8 (60,77/100)2 = 0,608.
6. Проверка условия устойчивости стойки (16.18)
σ = 180·10-3/(0,608·216·10-4) = 13,71 МПа ≈ Ryγc = 14 МПа.
Условие выполняется.
Пример 16.13. Для рамы, рассмотренной в примере 16.5 (см. рис.16.12, а), проверить устойчивость сжатой стойки сечение при F = 1860 кН, l = 4,5 м. Материал стойки – сталь марки С245 (Rу = 240 МПа). Сечение стойки – два рядом стоящих двутавра № 30 (A = 2·46,5 = 93 см2; Iz = 2·7080 = 14160 см4; iz = 12,3 см). Продольный изгиб стойки возможен параллельно стенкам двутавров. Коэффициент условия работы γс = 0,95.
Определить коэффициент запаса на устойчивость.
Решение.
1. Расчётная длина стойки (см. пример 16.5, п.7)
l0 = 0,946l = 0,946·4,5 = 4,26 м.
2. Гибкость стержня и соответствующий коэффициент продольного изгиба (см. прил. 15)
λ = l0 /iz = 426/12,3 = 34,6 < λcr =100, φ = 0,914.
3. Проверка условия устойчивости стойки (16.18)
σ = 1860·10-3/(0,914·93·10-4) = 218,82 МПа ≈ Ryγc = 228 МПа.
Условие выполняется.
4. Несущая способность сечения (16.19)
[N] = 0,914·93·10-4·0,95·240·103 = 1938 кН > N = 1860 кН.
5. Так как λ = 34,6 < λcr =100, критическую нагрузку определяем по формуле Ф. Ясинского.
Значение критического напряжения (16.15) при a = 310 МПа, b = 1.14 МПа, с = 0 (см. табл. 16.3)
σcr = 310 – 1,14·34,6 = 270,56 МПа.
7. Величина критической силы
Fcr = σcr A = 270,56·103·93·10-4 = 2516,2 кН.
8. Коэффициент запаса
kу = Fcr /[N] = 2516,2/1938 = 1,3.
Контрольные вопросы
Какое явление называется продольным изгибом центрально сжатого стержня?
Что называется потерей устойчивости?
Что называется критической силой?
Сформулируйте допущения, использумые при расчетах на устойчивость одиночных стержней и рам.
Сформулируйте статический критерий устойчивости.
Как определяется критическая сила для центрально сжатых прямолинейных стержней с конечным числом степеней свободы?
Как определяется критическая сила для центрально сжатых прямолинейных стержней с бесконечным числом степеней свободы?
Какое дифференциальное уравнение из теории изгиба лежит в основе вывода формулы Эйлера?
Какой вид имеет формула Эйлера?
Что называется расчетной длиной центрально сжатого стержня?
Что представляет собой коэффициент приведения длины, и чему он равен при различных условиях закрепления концов центрально сжатых стержней?
Как зависит величина критической силы от условий закрепления концов центрально сжатого стержня?
Запишите уравнение устойчивости в общем виде на основе метода перемещений.
Как получить таблицы реакций метода перемещений, используемые при расчете на устойчивость?
Какие упрощения возможны при расчете на устойчивость методом перемещений?
Какие формы потери устойчивости возможны в симметричных рамах?
От каких факторов расчетной схемы зависит минимальное значение критических си в симметричных рамах?
Что называется критическим напряжением?
Как устанавливается предел применимости формулы Эйлера?
Что называется предельной гибкостью?
При каких значениях гибкости стержня для определения критических напряжений используется формула Ясинского?
Как определяется критическая сила по Ясинскому?
Что называется коэффициентом продольного изгиба центрально сжатого стержня?
Как определяется коэффициент продольного изгиба?
Как подбирается сечение стержня при расчете на устойчивость?
Как определить несущую способность стержня при продольном изгибе?
Как проверить прочность стержня при продольном изгибе?
Глава 17 основы расчёта подпорных стен
17.1. Общие понятия
Подпорными стенами называют сооружения, предназначенные для удержания массы грунта или какого-либо сыпучего тела от обрушения, а также для восприятия напора воды в гидротехнических сооружениях.
Основные виды подпорных стен – массивные и тонкостенные. Массивные подпорные стены возводят из камня, бетона или бутобетона. Их отличает большой собственный вес G, который противодействует давлению грунта E (рис. 17.1, а).
К массивным подпорным стенам относятся: наружные стены подвалов (рис. 17.1, б), береговые устои мостов (рис. 17.1, в), набережные рек (рис. 17.1, г), ограждения горных дорог (рис. 17.1, д), плотины (рис. 17.1, е).
Тонкостенные подпорные стены выполняются из железобетона в виде тавра с неравными полками (рис. 17.2, а). На горизонтальные полки тавра передаётся вертикальное давление от грунта, что обеспечивает устойчивость стены в целом. Для уменьшения деформаций изгиба в тонких стенах такого типа при высоте более 4 м устраивают вертикальные контрфорсы на расстоянии 2 – 3 м друг от друга. К тонким подпорным стенам также относятся шпунтовые стены (рис. 17.2, б и в), выполняемые из ряда брусьев, досок или прокатной стали специального профиля. В зависимости от высоты шпунтовых стен и величины бокового давления грунта они могут быть свободно стоящие (рис. 17.2, б) и анкерные (рис. 17.2, в). Забиваемый в грунт шпунт может служить ограждением участка строительства при выемке котлована от сползания (обрушения) земляной массы или проникновения грунтовых вод.
Правильно спроектированная подпорная стена должна удовлетворять следующим условиям:
1. быть устойчивой от опрокидывания;
2. быть устойчивой против скольжения (для массивных стен);
3. напряжения в сечениях стены должны отвечать условиям прочности;
4. давление на грунт от массивных подпорных стен не должно превышать расчётного сопротивления грунта, определяемого СНиП.
Для расчёта любой подпорной стены необходимо определить давление грунта на стену. Точное определение этого давления является чрезвычайно трудной задачей в виду сложности учёта всех физико-механических характеристик грунтов. Поэтому в основу практических методов расчёта вводятся ниже перечисленные упрощения и допущения.
1. Грунты, оказывающие давление на подпорные стены, считаются идеально сыпучими телами, т.е. предполагается, что между частицами грунта отсутствуют силы сцепления. Основными характеристиками таких тел являются: объёмный вес грунта γ0 и угол естественного откоса φ0.
Если массу сыпучего тела высыпать на горизонтальную поверхность, то образуется объём с конической поверхностью, составляющей с горизонтом некоторый угол, который и называется углом естественного откоса или углом внутреннего трения.
В табл. 17.1 приведены ориентировочные значения объёмных весов и углов внутреннего трения для некоторых видов грунтов.
2. В основу определения воздействия сыпучего тела не подпорную стену положена теория предельного равновесия, предложенная Кулоном в 1776 г. и предполагающая, что:
сыпучее тело есть однородная сплошная среда, способная воспринимать лишь сдвигающие и сжимающие силы;
давление сыпучего тела определяется для момента, когда подпорная стена под действием этого давления начинает смещаться;
часть массива сыпучего тела (призма обрушения), которая начинает перемещаться вместе с подпорной стеной, считается абсолютно твёрдым телом, что позволяет применять для оценки её равновесия уравнения статики;
Таблица 17.1
Физико – механические характеристики грунтов
Вид грунта |
Объёмный вес γ0, (кН/м3) |
Угол внутреннего трения φ0 (град) |
Глина: мокрая влажная сухая Глинозём Гравий: мокрый сухой Земля растительная: мокрая влажная сухая Известняк дроблёный Камень Песок: мокрый влажный сухой Суглинок: мокрый влажный сухой Торф Шлак Щебень |
19 – 22 17 – 19 16 – 17 11 – 13
19 – 20 18
17 16 12 – 15 14 – 17 13 – 20
20 17 – 18 15 – 17
21 19 16 3 – 7 6 – 10 13 – 20 |
15 – 25 25 – 35 40 – 45 28 – 30
25 – 35 35 – 45
28 – 30 30 – 45 28 – 35 35 – 55 37
20 – 25 40 30 – 45
20 – 25 15 – 20 20 – 40 45 – 50 30 – 50 40 - 45 |
подпорная стена имеет неограниченную длину, остаётся в плане прямолинейной после деформации, а профиль сыпучего тела и все прочие условия постоянны по длине стены; это позволяет производить расчёт на 1 п.м. длины стены.
3. Как правило, для подпорных стен с вертикальной гранью соприкосновения с сыпучим телом пренебрегают трением между стеной и сыпучим телом.
17.2. Активное и пассивное давления на подпорную стену
Активным давлением сыпучего тела Ea называют то наибольшее воздействие, которое может оказать на подпорную стену масса сыпучего тела в момент начала процесса смещения стены, т.е. в момент её предельного равновесия.
Опытами установлено, что в момент начала сдвига подпорной стены от действия активного давления в сыпучем теле образуется область подвижки сыпучей массы, ограниченная криволинейной поверхностью AC (рис. 17.3), называемой поверхностью обрушения.
В целях упрощения расчётов принимается, что скольжение грунта происходит не по указанной криволинейной поверхности, а по плоскости AC, называемой плоскостью обрушения. Часть сыпучего тела, заключённая между внутренней поверхностью подпорной стены и плоскостью обрушения (призма ABC), называется призмой обрушения.
В том случае, если с другой стороны подпорной стены существует засыпка, то по мере возрастания активного давления стена испытывает отпор со стороны засыпки. Это противодействие продолжается до момента выпирания засыпки (грунта).
Наименьшее сопротивление, которое может оказать масса сыпучего тела на стену в условиях предельного равновесия, называется пассивным давлением Ep. Криволинейная поверхность A1C1 называется поверхностью выпирания, которая также в целях упрощения расчётов заменяется плоскостью выпирания A1C1. Соответственно, призма A1В1C1 называется призмой выпирания.
Угол θ наклона плоскости обрушения AC определяется из условия достижения величины активного давления наибольшей величины. При сползании призмы обрушения возникают силы трения по плоскостям AB и BC (рис. 17.4). Эти силы трения отклоняют реакции подпорной стены E и неподвижной части сыпучего тела R от нормалей к AB и AC соответственно на углы φs и φ0, где φs – угол трения сыпучего тела о материал стены.
В связи с принятыми выше допущениями, в дальнейшем будем считать поверхность стены идеально гладкой, т.е. φs = 0.
Рассмотрим простейший случай подпорной стены, когда её внутренняя поверхность AB вертикальна (рис. 17.5, а), поверхность грунта горизонтальна. Призма обрушения ABC, как твёрдое тело по принятому допущению, будет находиться в равновесии под действием трёх сил: собственного веса G0, реакции E подпорной стены и реакции неподвижной части сыпучей массы R. На основании условия равновесия трёх сил (§ 2.3.1) линии действия этих сил должны сходиться в одной точке, что при известных их направлениях позволяет построить замкнутый треугольник сил (рис.17.5, б).
Из построенного силового треугольника легко определяется реакция E. Но на основании аксиомы равенства действия и противодействия (см. подразд. 2.1, аксиома 5) величина активного давления Ea будет равна по величине и противоположна по направления реакции E, т.е.
Ea = G0 tg (θ − φ0). (17.1)
Входящий в выражение (17.1) вес призмы обрушения равен
G0 = γ0 A∆ABC = 0,5 γ0 h2ctg θ. (17.2)
Подставив (17.2) в (17.1), получим
Ea = 0,5γ0 h2 ctg θ·tg (θ − φ0). (17.3)
В выражении (17.3) переменной величиной является угол θ. Для определения максимального значения Ea возьмём первую производную от Ea по θ и приравняем её нулю
![]() .
.
Так как 0,5γ0 h2 ≠ 0, то должно равняться нулю выражение в квадратных скобках.
Тогда
![]() ,
,
или ·tg (θ − φ0)·cos2(θ − φ0) = sin θ·ctg θ.
Полученное равенство можно преобразовать, если принять
tg (θ − φ0) = sin (θ − φ0)/cos (θ − φ0); ctg θ =cos θ/sin θ
и умножить обе части полученного выражения на 2.
Тогда
2sin (θ − φ0)·cos (θ − φ0) = 2 sin θ·cos θ.
Так как левая и правая части полученного равенства выражают синусы двойного угла, то можно записать
sin 2(θ − φ0) = sin 2θ.
Последнее выражение справедливо в двух случаях:
(θ − φ0) = θ , что невозможно, так как заведомо φ0 ≠ 0;
2(θ − φ0) + 2θ = 180º.
Из второго условия определяем величину угла θ наклона плоскости обрушения
θ = 45º + 0,5 φ0.
Подставив полученное значение угла θ в (17.3), получим
Ea = 0,5γ0 h2 ctg (45º + 0,5 φ0)·tg (45º + 0,5 φ0 − φ0).
Произведя замену ctg (45º + 0,5 φ0) = tg (45º − 0,5 φ0), получим
Ea = 0,5γ0 h2 tg2(45º − 0,5 φ0).
Введём обозначение λa = tg2(45º − 0,5φ0) и назовём его коэффициентом активного давления. Формула для определения величины активного давления примет вид
Ea = 0,5γ0 h2 λa. (17.4)
Формула (17.4) показывает, что активное давление сыпучего тела на стену возрастает с увеличением его объёмного веса и высоты стены и с уменьшением угла естественного откоса. Указанная формула справедлива и в том случае, когда подпорная стена с внутренней стороны ограничена не вертикалью, а имеет вид уступов.
По аналогии, рассматривая равновесие призмы A1В1C1 (рис. 17.3), можно получить формулу для определения величины пассивного давления сыпучего тела, которая имеет вид:
Ep = 0,5γ0 h2 λp, (17.5)
где λp = tg2(45º + 0,5 φ0) – коэффициент пассивного давления.
Из сравнения формул (17.4) и (17.5) видно, что они отличаются лишь коэффициентами давления, т.е. при одинаковых значениях всех исходных данных, входящих в обе формулы, пассивное давления по величине будет больше. Эту особенность используют для повышения устойчивости подпорных стен путём увеличения их заглубления.
17.3. Эпюры интенсивности бокового давления
По формулам (17.4) и (17.5) определяют величины равнодействующих давлений сыпучего тела на стену. Но для проведения расчёта подпорной стены необходимо также знать давление сыпучего тела на любой её участок и точки приложения равнодействующих.
Будем полагать, что активное давление сыпучего тела на плоскость стены распределяется по всей её высоте h, и закон этого распределения нам пока неизвестен (кривая A1B на рис. 17.6, а). На глубине z рассмотрим бесконечно малый участок стены dz, на который действует элементарная величина давления
dEaz = qazdz,
где qaz – интенсивность давления на стену на глубине z.
В соответствии с (17.4)
Eaz = 0,5γ0 z2 λa.
Тогда величина интенсивности активного давления на глубине z
qaz= dEaz /dz = γ0 z λa. (17.6)
Формула (17.6) показывает, что распределение активного давления по высоте стены имеет линейный характер, и эпюра интенсивности активного давления (рис. 17.6, б) имеет вид треугольника, т.к.
при z = 0 qaz= 0, а при z = h qaz= qah= γ0 h λa.
Так как величина Ea является равнодействующей активного давления, то, очевидно, она должна проходить через центр тяжести эпюры давления, т.е. на расстоянии h/3 от основания стены.
По аналогии для пассивного давления имеем
qpz= γ0 z λp. (17.7)
Рассмотрим наиболее часто встречающиеся характерные случаи построения эпюр интенсивности давлений сыпучих тел на подпорные стены.
1. Многослойность массива сыпучего тела.
В том случае, когда массив сыпучего тела имеет многослойный характер (рис. 17.7, а), при котором каждый слой имеет свои характеристики, активное давление на стену определяют следующим образом.
Для каждого слоя строится эпюра интенсивности давлений по формуле (17.6) в предположении, что характеристики данного слоя действуют по всей высоте стены (рис. 17.7, б,в, и г), из которой выделяется только участок, соответствующий высоте данного слоя. Полученные таким образом участки объединяются в общую эпюру интенсивности давлений (рис.17.7, д). Равнодействующие активного давления Ea1, Ea2, Ea3,… Ean по слоям определяются как площади отдельных участков эпюры давлений. Точки приложения этих равнодействующих определяются как центры тяжести участков эпюры давлений zc1, zc2,… zcn:
Для любого i – того слоя
 ,
(17.8)
,
(17.8)
где hi–
высота i
– того слоя;
![]() − общая высота предыдущих слоёв.
− общая высота предыдущих слоёв.
2. Влияние временной равномерно распределённой нагрузки на поверхности сыпучего массива.
Принимаем, что временная равномерно распределённая нагрузка q (кН/м2) приложена в пределах призмы обрушения (рис. 17.8). Заменим действие этой нагрузки воображаемым (эквивалентным) слоем сыпучего тела высотой
h0 = q/γ0, (17.9)
где γ0 – объёмный бес сыпучего тела, поддерживаемого стеной.
Чтобы поддержать эквивалентный слой сыпучего тела, необходимо увеличить высоту подпорной стены на величину h0. Для такой подпорной стены с высотой (h + h0) эпюра интенсивности давлений будет иметь вид треугольника ADA1, построенного по зависимости (17.6). Следовательно, для заданной подпорной стены высотой эпюра интенсивности давлений будет иметь вид трапеции ABB1A1.
Таким образом, интенсивность активного давления будет изменяться по закону
qaz = (q + γ0 z) λa (17.10)
и её характерные ординаты будут:
при z = 0 qaz= q, а при z = h qaz= qah= (q +γ0 h) λa.
Прямая B1A1 эпюры интенсивности давления ограничивает ординаты давления по высоте стены с учётом влияния временной нагрузки q; параллельная ей прямая BA2 ограничивает эпюру интенсивности давления при отсутствии временной нагрузки на поверхности. Разность ординат этих эпюр составляет величину временной нагрузки q.
Равнодействующая активного давления сыпучего тела на подпорную стену равно площади трапеции ABB1A1. Точкой её приложения является центр тяжести трапеции, положение которого по формуле (17.8)
![]() .
.
По аналогии для пассивного давления
qpz = (q + γ0 z) λp. (17.11)
17.4. Проверка устойчивости и прочности подпорных стен
Расчёт подпорной стены из условия устойчивости на опрокидывание.
Подпорная стена должна быть устойчива от опрокидывания относительно нижнего наружного ребра К (рис. 17.9, а). Проверка устойчивости стены на опрокидывание производится чаще всего в случае возведения стены на скальном основании или бетонной плите, а также тогда, когда отсутствует массив сыпучего тела, создающий пассивное давление на стену.
Активное давление Ea стремится опрокинуть стену, а удерживающими факторами от опрокидывания являются вес стены G и пассивное давление Ep (рис. 17.9, б).
Опрокидывающий момент вокруг оси, совпадающей с наружным ребром К, равен
Mt =Eazc, (17.12)
а удерживающий момент, препятствующий опрокидыванию,
Mr =G·xc + Epz´c. (17.13)
Устойчивость подпорной стены на опрокидывание определяет коэффициент запаса устойчивости на опрокидывание
kt = Mr / Mt ≥ 1,5. (17.14)
2. Расчёт подпорной стены из условия устойчивости на сдвиг (скольжение).
Предполагаемый сдвиг происходит параллельно подошве подпорной стены (рис. 17.10, а). Сдвигающей силой Fsa является активное давление на подпорную стену Ea (рис. 17.10, б).
Препятствием сдвигу является сумма удерживающих сил
∑Fsr = (G + ∑Gi0)tg φ0 + Ac0 + Ep, (17.15)
где: G − вес подпорной стены;
∑Gi0 − вес грунта на уступах подпорной стены;
A − расчётная площадь основания подпорной стены;
c0 − удельное сцепление грунта под подошвой стены, определяемое согласно СНиП 2.02.01 – 83*;
Ep − пассивное давление грунта.
Устойчивость подпорных стен против сдвига по подошве определяется коэффициентом запаса устойчивости на сдвиг
ks = ∑Fsr/Fsa ≥ 1,5. (17.16)
При этом стены с горизонтальной подошвой рассчитываются по трём вариантам сдвига (рис. 17.10, в): β1 = 0, β2 = 0,5φ0 и β3 = φ0. Равнодействующая пассивного давления грунта Ep вычисляется для слоя грунта hi, соответствующего углу βi.
3. Расчёт подпорной стены из условия прочности.
Подпорные стены должны быть не только устойчивы, но и должна быть обеспечена их прочность. Для любого сечения стены от действия вертикальных (вес стены) и горизонтальных (давление на стену) сил всегда можно найти изгибающий момент M и вертикальную сжимающую силу N. В этом случае напряжения в сечении стены можно определить по формуле внецентренного сжатия (11.17)
![]() ,
,
где A – площадь сечения;
e = M/N – эксцентриситет силы N относительно центра сечения;
b – ширина стены в сечении.
Учитывая, что обычно ведётся расчёт для 1 п.м. стены и A = b·1 = b, формула для определения нормальных напряжений примет вид:
![]() .
(17.17)
.
(17.17)
Условие прочности стены выполняется, если σmax ≤ R, где R – расчётное сопротивление материала стены. При безусловном выполнении условия прочности необходимо, чтобы в сечении возникали напряжения только одного знака. Как было показано в подразд. 11.3, данное условие соблюдается, когда сила N находится в пределах ядра сечения, т.е. при e ≤ b/6 (см. рис.11.13, а).
При определении напряжений по подошве подпорной стены в случае когда e > b0/6 возникают растягивающие напряжения, которые грунтом не воспринимаются. Поэтому положительный участок эпюры напряжений отбрасывается (рис. 17.11).
В этом случае нормальное суммарное давление на подошву Nп должно уравновешиваться равнодействующей напряжений в грунте Rгр. Из эпюры напряжений находим
Rгр = Nп = 0,5с· σmax,
откуда σmax = 2Nп /с ≤ R0, (17.18)
где R0 – расчётное сопротивление грунта; с = 3(0,5b0 – e ).
При e > b0/6 осадка стены становится неравномерной. Этого следует избегать. Нормами установлено, что при отсутствии специальных технологических требований расчёт по деформациям считается удовлетворительным, если среднее напряжение в грунте не превышает его расчётного сопротивления, а максимальное напряжение не больше 1,2 R0, т.е.
σср = 0,5σmax ≤ R0, (17.19)
σmax ≤ 1,2R0. (17.20)
Пример 17.1. Проверить устойчивость подпорной стены (рис. 17.12) на опрокидывание и сдвиг по подошве. Стена изготовлена из тяжёлого бетона с объёмным весом 22 кН/м3. Удельное сцепление грунта под подошвой стены c0 = 39 кПа.
Решение.
Определяем активное давление грунта на подпорную стену.
1.1. Толщина эквивалентного слоя грунта (17.9):
по отношению к первому слою грунта h01 = 27/18 = 1,5 м;
по отношению ко второму слою h02 = 27/20 = 1,35 м.
Коэффициенты активного давления
по первому слою грунта λa1= tg2(45º – φ01) = 0,271;
по второму слою λa2= tg2(45º – φ02) = 0,427.
1.3. Ординаты эпюры интенсивности активных давлений (17.10)
по первому слою грунта:
z = 0; qa = 27·0,271 = 7,32 кПа;
z = 5,5 м; qa = (27 + 18·5,5)0,271 = 37,13 кПа;
по второму слою грунта
z = 5,5 м; qa = (27 + 20·5,5)0,427 = 58,5 кПа;
z = 9,9 м; qa = (27 + 20·9,9)0,427 = 96,08 кПа.
1.4. Величины активных давлений и центры тяжести их приложений (17.8):
по первому слою грунта Ea1 = 0,5(7,32 + 37,13) = 122,24 кН/м;
 м;
м;
по второму слою грунта Ea2 = 0,5(58,5 + 96,08) = 340,08 кН/м;
 м.
м.
2. Определяем пассивное давление грунта (17.11):
λp= tg2(45º + φ02) = 2.37;
qp = 22·2,4·2,37 = 113,76 кПа;
Ep = 0,5·2,4·113.76 = 136.51 кН/м;
z´c = 2,4/3 = 0,8 м.
Нормативный вес 1 п.м. стены по участкам (рис. 17.12) и общий вес:
G1 = 22·0,5·7,5·2,4 = 198 кН;
G2 = 22·2,4·6 = 316,8 кН;
G3 = 22·7,5·3,6 = 594 кН;
G = 198 + 594 + 316,8 = 1108,8 кН.
4. Проверка устойчивости стены на опрокидывание вокруг грани K:
4.1. Опрокидывающий момент (17.12)
Mt = 122,4(2,16 + 4,4) + 340,08·2,07 = 1502,46 кН·м.
4.2. Удерживающий момент (17.13)
Mr = 136.51·0,8 + 198·1,6 + 594·3,2 + 316,8·3 = 3277,2 кН·м.
4.3. Коэффициент устойчивости на опрокидывание (17.14)
kt = 3277,2/1502,46 = 2,18 > 1.5,
т.е. стена на опрокидывание устойчива.
5. Проверка устойчивости стены на сдвиг по подошве:
5.1. Сдвигающая сила от активного давления
Fsa = 122,24 + 340,08 = 462,32 кН.
5.2. Сумма удерживающих сил (17.15)
∑Fsr = 1108,8·tg (0,5φ02) + 39·6 + 136,51 = 616,19 кН.
5.3. Коэффициент устойчивости на сдвиг (17.16)
kt = 616,19/462,32 = 1,31 < 1.5,
т.е. запас устойчивости стены на сдвиг недостаточен, необходимо увеличение суммы удерживающих сил, например, за счёт увеличения веса.
17.5. Понятие о расчёте тонкостенных подпорных стен
Железобетонные тонкие подпорные стены (рис.17.2, а) могут быть как монолитными, так и сборными. Их применение выгодно, так значительно, в три - четыре раза, сокращает расход материала по сравнению с массивными стенами.
Расчёт активного и пассивного давлений на тонкие стены ничем не отличается от рассмотренных выше массивных стен.
Железобетонные тонкие подпорные стены чаще всего имеют поперечные сечения в форме тавра и состоят из лицевой плиты, удерживающей засыпку и фундаментной плиты.
Если подпорная стена имеет высоту до 4 – 5 м, то обычно она изготавливается без контрфорсов. А этом случае лицевая плита рассчитывается как простая консоль шириной 1 м на действие боковой распределённой нагрузки. При высоте стены более 5 м при наличии контрфорсов лицевая плита рассчитывается как многопролётная неразрезная плита, опорами которой являются контрфорсы.
Фундаментные плиты тонких подпорных стен рассчитываются на нагрузку от давления грунта на основание стены, причём и левую, и правую части фундаментной плиты рассчитывают как консоли.
Контрольные вопросы
Какие сооружения называют подпорными стенами?
Каким условиям должна удовлетворять подпорная стена?
Какие упрощения и допущения положены в основу практических расчетов подпорных стен?
Что называется углом естественного откоса грунта?
Что называется активным и пассивным давлениями грунта на подпорную стену?
Что положено в основу определения воздействия грунта на подпорную стену?
Сформулируйте основные положения теории предельного равновесия грунта.
Что называется поверхностью обрушения грунта?
Что представляют собой коэффициенты активного и пассивного давления?
В чем состоит расчет подпорной стены на прочность и устойчивость?
Приложения
Приложение 1
Модули упругости и коэффициенты Пуассона
Материал |
Модули упругости E, Eb, E0, МПа |
Модуль сдвига G, МПа |
Коэффициент Пуассона μ |
Сталь прокатная |
2,06·105 |
7,8·104 |
0,24…0,3 |
Чугун |
(0.83…0,98)·105 |
4,5·104 |
0,23…0,27 |
Алюминиевые сплавы |
0,7·105 |
2,6·104 |
0,32…0,34 |
Медь, латунь, бронза |
(1…1,3)·105 |
(3,5…4)·104 |
0,31…0,34 |
Стекло |
0,56·105 |
2,2·104 |
0,25 |
Гранит |
0,49·105 |
2·104 |
0,08…0,15 |
Известняк |
0,42·105 |
1,1·104 |
0,2…0,3 |
Мрамор |
0,56·105 |
1,9·104 |
0,15…0,22 |
Песчаник |
0,18·105 |
– |
– |
Каменная кладка: |
|
|
|
из гранита |
0,1·105 |
– |
– |
из известняка |
0,06·105 |
– |
– |
из кирпича |
(0,027…0,03)·105 |
– |
– |
Бетон класса: |
|
|
|
В 20 |
0,27·105 |
0,4Eb |
0,16…0,18 |
В 30 |
32,5·105 |
0,4Eb |
0,16…0,18 |
В 50 |
0,39·105 |
0,4Eb |
0,16…0,18 |
Дерево (сосна, ель) |
|
|
|
вдоль волокон |
(0,1…0,12)·105 |
5.5·104 |
– |
поперёк волокон |
(0,005…0,01)·105 |
– |
– |
Текстолит |
(0,06…0,1)·105 |
0,25·104 |
– |
Полимербетон |
(0,18…0,2)·105 |
– |
– |
Приложение 2
Расчётные сопротивление проката для стальных конструкций
и отливок из серого чугуна
Материал |
Расчётные сопротивления, МПа |
|||
Ry |
Ru |
Rt |
Rc |
|
Сталь листовая, прокатная, фасонная: |
|
|
|
|
C245 |
240 |
360 |
– |
– |
C255 |
240 |
360 |
– |
– |
C285 |
280 |
390 |
– |
– |
C375 |
345 |
480 |
– |
– |
Чугун серый: |
|
|
|
|
СЧ15 |
– |
– |
55 |
160 |
СЧ20 |
– |
– |
65 |
200 |
СЧ25 |
– |
– |
85 |
230 |
СЧ39 |
– |
– |
100 |
250 |
Приложение 3
Расчётные сопротивления бетона, камня и кирпичной кладки
Материал |
Расчётные сопротивления, МПа |
||||
Radm |
Rtb |
R |
Rb |
Rbt |
|
Бетон тяжёлый класса: |
|
|
|
|
|
В 20 |
– |
– |
– |
11,5 |
0,9 |
В 30 |
– |
– |
– |
17,0 |
1,2 |
В 50 |
– |
– |
– |
27,5 |
1,55 |
Кладка из глиняного кирпича: |
|
|
|
|
|
марки 100 |
– |
– |
1,5 |
– |
– |
марки 125 |
– |
– |
2,0 |
– |
– |
Известняк |
15-200 |
<0,29 |
– |
– |
– |
Гранит |
100-320 |
– |
– |
– |
– |
Мрамор |
100-300 |
– |
– |
– |
– |
Гипс |
4-12 |
– |
– |
– |
– |
Бут – известняк |
10-70 |
– |
– |
– |
– |
Бутовая кладка их рваного бута |
|
|
|
|
|
М 800 на растворе М 100 |
– |
– |
2,2 |
– |
– |
Стекло |
600-1200 |
– |
– |
– |
– |
Приложение 4
Расчётные сопротивления для некоторых сортов древесины
Напряжённое состояние и характеристики элементов |
Расчётные сопротивления, МПа |
||
сосна, ель |
дуб |
бук |
|
1. Изгиб Rи, сжатие Rс и смятие Rсм |
|
|
|
вдоль волокон: |
|
|
|
элементы прямоугольного сечения |
14 |
18,2 |
15,4 |
элементы из круглых пиломатериалов |
16 |
20,8 |
17,6 |
2. Растяжение вдоль волокон Rр |
10 |
13 |
11 |
3. Сжатие Rс90 и смятие Rсм90 по всей |
|
|
|
площади поперёк волокон |
1,8 |
3,6 |
2,9 |
4. Смятие поперёк волокон Rсм90, местное |
|
|
|
и опорных частей |
3 |
6 |
4,8 |
5. Сдвиг вдоль волокон Rск: |
|
|
|
при изгибе неклеенных элементов |
1,8 |
2,34 |
2,34 |
в лобовых врубках |
2,4 |
3,1 |
3,1 |
6. Сдвиг поперёк волокон Rск90 |
1 |
1,3 |
1,3 |
Приложение 5
Геометрические характеристики некоторых плоских сечений
|
1.Квадрат
A=a2;
Iz
= Iy
= Wz
=Wy
=
|
|
2. Прямоугольник
A=bh;
Iz
=
Wz
= |
|
3. Прямоугольный треугольник
A=0,5bh;
Iz
=
Wzн
= Wzв
= |
|
4. Равнобедренный треугольник
A=0,5bh;
Iz
=
;
Iy
= Wzн = (для нижних волокон); Wy = ; Wzв = (для верхних волокон); iz = . |
Окончание прил. 5
|
5. Короб
A=bh–
b1h1;
Iz
=
Wz
=
|
|
6. Симметричный двутавр
A=bh–b1h1;
Iz
=
;
Iy
=
Wz
=
;
Wy
=
|
|
7. Круг
A=πr2;
Iz
=
Iy
= Wz
=
Wy
= |
|
8. Кольцо α=r1/r; A= πr2(1–α2); Iz = Iy = (1–α4); Iρ0=2 Iz = (1–α4); Wz
= Wy
=
(1–α4);
iz
= iy
= |
Приложение 6
Двутавры горячекатаные (по ГОСТ 8239 – 89)
|
h –высота двутавра; b – ширина полки; s – толщина стенки; t– средняя толщина полки; A – площадь поперечного сечения; |
I – момент инерции сечения; W – момент сопротивления; S – статический момент половины сечения; i – радиус инерции.
|
|||||||||||
№ двутавра |
Масса 1 п.м., кг |
Размеры, мм |
A, см2 |
Iz, см4 |
Wz, см3 |
iz, см |
Sz, см3 |
Iy, см4 |
Wy, см3 |
iy, см |
|||
h |
b |
s |
t |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
10 12 14 16 18 |
9,46 11,5 13,7 15,9 18,4 |
100 120 140 160 180 |
55 64 73 81 90 |
4,5 4,8 4,9 5 5,1 |
7,2 7,3 7,5 7,8 8,1 |
12 14,7 17,4 20,2 23,4 |
198 350 572 873 1280 |
39,7 58,4 81,7 109 143 |
4,06 4,88 5,73 6,57 7,42 |
23 33,7 46,8 62,3 81,4 |
17,9 27,9 41,9 58,6 82,6 |
6,49 8,72 11,5 14,5 18,4 |
1,22 1,38 1,55 1,7 1,88 |
Окончание прил. 6
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
20 22 24 27 30 33 36 40 45 50 55 60 |
21 24 27,3 31,5 365 42,2 48,6 57 66,5 78,5 92,6 108 |
200 220 240 270 300 330 360 400 450 500 550 600 |
100 110 115 125 135 140 145 155 160 170 180 190 |
5,2 5,4 5,6 6 6,5 7 7,5 8,3 9 10 11 12 |
8,4 8,7 9,5 9,8 10,2 11,2 12,3 13 14,2 15,2 16,5 17,8 |
26,8 30,6 34,8 40,2 46,5 53,8 61,9 72,6 84,7 100 118 138 |
1840 2550 3460 5010 7080 9840 13380 19062 27696 39727 55962 76806 |
184 232 289 371 472 597 743 953 1231 1589 2035 2560 |
8,28 9,13 9,97 11,2 12,3 13,5 14,7 16,2 18,1 19,9 21,8 23,6 |
104 131 163 210 268 339 423 545 708 919 1181 1491 |
115 157 198 260 337 419 516 667 808 1043 1356 1725 |
23,1 28,6 34,5 41,5 49,9 59,9 71,1 86,1 101 123 151 182 |
2,07 2,27 2,37 2,54 2,69 2,79 2,89 3,03 3,09 3,23 3,39 3,54 |
Приложение 7
Швеллеры горячекатаные (по ГОСТ 8240 -89)
|
h –высота швеллера; b – ширина полки; s – толщина стенки; t– средняя толщина полки; A – площадь поперечного сечения; |
I – момент инерции сечения; W – момент сопротивления; S – статический момент половины сечения; i – радиус инерции; z0 – расстояние от оси у до наружной грани стенки.
|
||||||||||||
№ швеллера |
Масса 1 п.м., кг |
Размеры, мм |
A, см2 |
Iz, см4 |
Wz, см3 |
iz, см |
Sz, см3 |
Iy, см4 |
Wy, см3 |
iy, см |
z0, см |
|||
h |
b |
s |
t |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
5 6,5 8 10 |
4,84 5,9 7,05 8,59 |
50 65 80 100 |
32 36 40 46 |
4,4 4,4 4,5 4,5 |
7 7,2 7,4 7,6 |
6,16 7,51 8,98 10,9 |
22,8 48,6 89,4 174 |
9,1 15 22,4 34,8 |
1,92 2,54 3,16 3,99 |
5,59 9 13,3 20,4 |
5,61 8,7 12,8 20,4 |
2,75 3,68 4,75 6,46 |
0,95 1,08 1,19 1,37 |
1,16 1,24 1,31 1,44 |
Окончание прил. 7
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
12 14 16 16а 18 18а 20 22 24 27 30 33 36 40 |
10,4 12,3 14,2 15,3 16,3 17,4 18,4 21 24 27,7 31,8 36,5 41,9 48,3 |
120 140 160 160 180 180 200 220 240 270 300 330 360 400 |
52 58 64 68 70 74 76 82 90 95 100 105 110 115 |
4,8 4,9 5 5 5,1 5,1 5,2 5,4 5,6 6 6,5 7 7,5 8 |
7,8 8,1 8,4 9 8,7 9,3 9 9,5 10 10,5 11 11,7 12,6 13,5 |
133 15,6 18,1 19,5 20,7 22,2 23,4 26,4 30,6 35,2 40,5 46,5 53,4 61,5 |
304 491 747 823 1090 1190 1520 2110 2900 4160 5810 7980 10820 15220 |
50,6 70,2 93,4 103 121 132 152 192 242 308 387 484 601 761 |
4,78 5,6 6,42 6,49 7,24 7,32 8,7 8,89 9,73 10,9 12 13,1 14,2 15,7 |
29,6 40,8 54,1 59,4 69,8 76,1 87,8 110 139 178 224 281 350 444 |
31,2 45,4 63,3 78,8 86 105 113 151 208 262 327 410 513 642 |
8,52 11 13,8 16,4 17 20 20,5 25,1 31,6 37,3 43,6 51,8 61,7 73,4 |
1,53 1,7 1,87 2,01 2,04 2,18 2,2 2,37 2,6 2,73 2,84 2,97 3,1 3,23 |
1,54 1,67 1,8 2 194 2,13 2,07 2,21 2,42 2,47 2,52 2,59 2,68 2,75 |
Приложение 8
Уголки стальные горячекатаные неравнополочные (по ГОСТ 6510 – 86)
|
B – ширина большой полки; b – ширина меньшей полки; t – толщина полки; A – площадь поперечного сечения; I – момент инерции сечения; |
Izy – центробежный момент инерции; i – радиус инерции; α – угол наклона главной центральной оси; z0, y0 – расстояние от центра тяжести до наружных граней полок. |
|||||||||||||
№ уголка |
Масса 1 п.м., кг |
Размеры, мм |
A, см2 |
Iz, см4 |
iz, см |
Iy, см4 |
iy, см |
Iumin, см4 |
iumin, см |
tg α |
см4 |
z0, см |
y0, см |
||
B |
b |
t |
|||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
5/3,2 |
2,4 |
50 |
32 |
4 |
3,17 |
7,9 |
1,59 |
2,56 |
0,9 |
1,52 |
0,69 |
0,401 |
2,59 |
0,76 |
1,65 |
7,5/5 |
4,79 |
75 |
50 |
5 |
6,11 |
34,8 |
2,39 |
12,5 |
1,43 |
7,24 |
1,09 |
0,436 |
12 |
1,17 |
2,39 |
9/5,6 |
6,7 |
90 |
56 |
6 |
8,54 |
70,6 |
2,88 |
21,2 |
1,58 |
12,7 |
1,22 |
0,384 |
22,5 |
1,28 |
2,95 |
10/6,3 |
7,53 8,7 9,87 |
100 |
63 |
6 7 8 |
9,58 11,1 12,6 |
98,3 113 127 |
3,2 3,19 3,18 |
30,6 35 39,2 |
1,79 1,78 1,77 |
18,2 208 23,4 |
1,38 1,37 1,36 |
0,393 0,392 0,391 |
31,5 36,1 40,5 |
1,42 1,46 1,5 |
3,23 3,28 3,32 |
Окончание прил. 8
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
11/7 |
10,9 |
110 |
70 |
8 |
13,9 |
172 |
3,51 |
54,6 |
1,98 |
32,3 |
1,52 |
0,4 |
55,9 |
1,64 |
3,61 |
12,5/8 |
11 12,6 15,5 |
125 |
80 |
7 8 10 |
14,1 16 19,7 |
227 256 312 |
4,01 4 3,98 |
73,7 83 100 |
2,29 2,28 2,26 |
43,4 48,8 59,3 |
1,76 1,75 1,74 |
0,407 0,408 0,404 |
74,7 84,1 102 |
1,8 1,84 1,92 |
4,01 4,05 4,14 |
14/9 |
14,1 17,5 |
140 |
90 |
8 10 |
18 22,2 |
364 444 |
4,49 4,47 |
120 146 |
2,58 2,56 |
70,3 85,3 |
1,98 1,96 |
0,411 0,409 |
121 147 |
2,03 2,12 |
4,49 4,58 |
16/10 |
18 19,8 23,6 |
160 |
100 |
9 10 12 |
22,9 25,3 30 |
606 667 784 |
5,15 5,13 5,11 |
186 204 239 |
2,85 2,84 2,82 |
110 121 142 |
2,2 2,19 2,18 |
0,391 0,39 0,388 |
194 213 249 |
2,24 2,28 2,36 |
5,19 5,23 5,32 |
18/11 |
22,2 26,4 |
180 |
110 |
10 12 |
28,3 33,7 |
952 1123 |
5,8 5,77 |
275 324 |
3,12 3,1 |
165 194 |
2,42 2,4 |
0,376 0,374 |
295 348 |
2,44 2,52 |
5,88 5,97 |
20/12,5 |
27,4 29,7 34,4 39,1 |
200 |
125 |
11 12 14 16 |
34,9 37,9 43,9 49,8 |
1449 1568 1801 2026 |
6,45 6,43 6,41 6,38 |
446 482 551 617 |
3,58 3,57 3,54 3,52 |
264 285 327 367 |
2,75 2,74 2,73 2,72 |
0,392 0,392 0,39 0,388 |
465 503 573 643 |
2,79 2,83 2,91 2,99 |
6,5 6,54 6,62 6,71 |
Приложение 9
Уголки горячекатаные равнополочные (по ГОСТ 8509 – 93)
|
b – ширина меньшей полки; t – толщина полки; A – площадь поперечного сечения; I – момент инерции сечения; |
Izy – центробежный момент инерции; i – радиус инерции; z0 – расстояние от центра тяжести до наружной грани полки. |
||||||||||
№ уголка |
Масса 1 п.м., кг |
Размеры, мм |
A, см2 |
Iz, см4 |
iz, см |
см4 |
см |
см4 |
см |
, см4 |
z0, см |
|
b |
t |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
5 |
3,05 3,77 |
50 |
4 5 |
3,89 4,8 |
9,21 11,2 |
1,54 1,53 |
14,6 17,8 |
1,94 1,92 |
3,8 4,63 |
0,99 0,98 |
5,42 6,57 |
1,38 1,42 |
5,6 |
3,44 4,25 |
56 |
4 5 |
4,38 5,41 |
13,1 16 |
1,73 1,72 |
20,8 25,4 |
2,18 2,16 |
5,41 6,59 |
1,11 1,1 |
7,69 9,41 |
1,52 1,57 |
Продолжение прил. 9
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
6,3 |
3,9 4,81 5,72 |
63 |
4 5 6 |
4,96 6,13 7,28 |
18,9 23,1 27,1 |
1,95 1,94 1,93 |
29,9 36,8 42,9 |
2,45 2,44 2,43 |
7,81 9,52 11,2 |
1,25 1,25 1,24 |
11 13,7 15,9 |
1,69 1,74 1,78 |
7 |
5,38 6,39 |
70 |
5 6 |
6,86 8,15 |
31,9 37,8 |
2,16 2,15 |
50,7 59,6 |
2,72 2,71 |
13,2 15,5 |
1,39 1,38 |
18,7 22,1 |
1,9 1,94 |
7,5 |
5,8 6,89 7,96 |
75 |
5 6 7 |
7,39 8,78 10,1 |
39,5 46,6 53,3 |
2,31 2,3 2,29 |
62,6 73,9 84,6 |
2,91 2,9 2,89 |
16,4 19,3 22,1 |
1,49 1,48 1,48 |
23,1 27,3 31,2 |
2,02 2,6 2,1 |
8 |
7,36 8,51 |
80 |
6 7 |
9,38 10,8 |
57 65,3 |
2,47 2,45 |
90,4 104 |
3,11 3,09 |
23,5 27 |
1,58 1,58 |
33,4 38,3 |
2,19 2,23 |
9 |
8,33 9,64 10,9 |
90 |
6 7 8 |
10,6 12,3 13,9 |
82,1 94,3 106 |
2,78 2,77 2,76 |
130 150 168 |
3,5 3,49 3,48 |
34 38,9 43,8 |
1,79 1,78 1,77 |
48,1 55,4 62,3 |
2,43 2,47 2,51 |
Окончаение прил. 9
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
10 |
10,8 12,2 15,1 17,9 |
100 |
7 8 10 12 |
13,8 15,6 19,2 22,8 |
131 147 179 209 |
3,08 3,07 3,05 3,03 |
207 233 284 331 |
3,88 3,87 3,84 3,81 |
54,2 609 74,1 86,9 |
1,98 1,98 1,96 1,95 |
76,4 86,3 11 122 |
2,71 2,75 2,83 2,91 |
11 |
11,9 13,5 |
110 |
7 8 |
15,2 17,2 |
176 198 |
3,4 3,39 |
279 315 |
4,29 4,28 |
72,7 81,8 |
2,19 2,18 |
106 116 |
2,96 3 |
12,5 |
15,5 17,3 19,1 22,7 |
125 |
8 9 10 12 |
19,7 22 24,3 28,9 |
294 327 360 422 |
3,87 3,86 3,85 3,82 |
467 520 571 670 |
4,87 4,86 4,84 4,82 |
122 136 149 174 |
2,49 2,48 2,47 2,46 |
172 192 211 248 |
3,36 3,4 3,45 3,53 |
Приложение 10
Таблицы реакций и усилий в изгибаемых стержнях
От единичных смещений связей

Приложение 11
Таблицы реакций и усилий в изгибаемых стержнях
От внешних воздействий

Приложение 12
Таблицы реакций в сжато-изогнутых стержнях от единичных
Смещений при расчёте на устойчивость

Приложение 13
Таблица значений функций метода
перемещений для сжато-изогнутых стержней
|
|
|
|
|
|
|
0,0 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
0,2 |
0,9973 |
0,9980 |
1,0009 |
0,9992 |
0,9840 |
0,9959 |
0,4 |
0,9895 |
0,9945 |
1,0026 |
0,9973 |
0,9362 |
0,9840 |
0,6 |
0,9856 |
0,9881 |
1,0061 |
0,9941 |
0,8557 |
0,9641 |
0,8 |
0,9566 |
0,9787 |
1,0111 |
0,9895 |
0,7432 |
0,9362 |
1,0 |
0,9313 |
0,9662 |
1,0172 |
0,9832 |
0,5980 |
0,8999 |
1,1 |
0,9194 |
0,9590 |
1,0209 |
0,9798 |
0,5131 |
0,8789 |
1,2 |
0,8998 |
0,9511 |
1,0251 |
0,9751 |
0,4198 |
0,8557 |
1,3 |
0,8814 |
0,9424 |
1,0298 |
0,9715 |
0,3181 |
0,8307 |
1,4 |
0,8613 |
0,9329 |
1,0348 |
0,9669 |
0,2080 |
0,8035 |
1,5 |
0,8393 |
0,9226 |
1,0403 |
0,9619 |
0,0893 |
0,7743 |
1,6 |
0,8153 |
0,9116 |
1,0463 |
0,9566 |
-0,0380 |
0,7432 |
1,7 |
0,7891 |
0,8998 |
1,0529 |
0,9509 |
-0,1742 |
0,7100 |
1,8 |
0,7609 |
0,8871 |
1,0600 |
0,9448 |
-0,3191 |
0,6747 |
1,9 |
0,7297 |
0,8735 |
1,0676 |
0,9382 |
-0,4736 |
0,6374 |
2,0 |
0,6961 |
0,8590 |
1,0760 |
0,9313 |
-0,6372 |
0,5980 |
2,1 |
0,6597 |
0,8437 |
1,0850 |
0,9240 |
-0,8103 |
0,5565 |
2,2 |
0,6202 |
0,8273 |
1,0946 |
0,9164 |
-0,9931 |
0,5131 |
2,3 |
0,5772 |
0,8099 |
1,1050 |
0,9083 |
-1,1861 |
0,4675 |
2,4 |
0,5304 |
0,7915 |
1,1164 |
0,8998 |
-1,3895 |
0,4198 |
2,5 |
0,4793 |
0,7720 |
1,1286 |
0,8909 |
-1,6040 |
0,3701 |
2,6 |
0,4234 |
0,7513 |
1,1417 |
0,8814 |
-1,8299 |
0,3181 |
2,7 |
0,3621 |
0,7294 |
1,1559 |
0,8716 |
-2,0679 |
0,5565 |
2,8 |
0,2944 |
0,7064 |
1,1712 |
0,8613 |
-2,3189 |
0,2080 |
2,9 |
0,2195 |
0,6819 |
1,1878 |
0,8506 |
-2,5838 |
0,1498 |
3,0 |
0,1361 |
0,6560 |
1,2057 |
0,8393 |
-2,8639 |
0,0893 |
Продолжение прил.13
|
|
|
|
|
|
|
3,1 |
0,0424 |
0,6287 |
1,2252 |
0,8275 |
-3,1609 |
0,0207 |
3,2 |
-0,0635 |
0,5997 |
1,2463 |
0,8153 |
-3,4763 |
-0,0380 |
3,3 |
-0,1847 |
0,5691 |
1,2691 |
0,8024 |
-3,8147 |
-0,1051 |
3,4 |
-0,3248 |
0,5366 |
1,2940 |
0,7891 |
-4,1781 |
-0,1742 |
3,5 |
-0,4894 |
0,5021 |
1,3212 |
0,7751 |
-4,5727 |
-0,2457 |
3,6 |
-0,6862 |
0,4656 |
1,3508 |
0,7609 |
-5,0062 |
-0,3191 |
3,7 |
-0,9270 |
0,4265 |
1,3834 |
0,7457 |
-5,4903 |
-0,3951 |
3,8 |
-1,2303 |
0,3850 |
1,4191 |
0,7297 |
-6,0436 |
-0,4736 |
3,9 |
-1,6268 |
0,3407 |
1,4584 |
0,7133 |
-6,6968 |
-0,5542 |
4,0 |
-2,1726 |
0,2933 |
1,5018 |
0,6961 |
-7,5058 |
-0,6372 |
4,1 |
-2,9806 |
0,2424 |
1,5501 |
0,6783 |
-8,5836 |
-0,7225 |
4,2 |
-4,3155 |
0,1877 |
1,6036 |
0,6597 |
-10,196 |
-0,8103 |
4,3 |
-6,9949 |
0,1288 |
1,6637 |
0,6404 |
-13,158 |
-0,9004 |
4,4 |
-15,330 |
0,0648 |
1,7310 |
0,6202 |
-27,781 |
-0,9931 |
4,5 |
227,80 |
-0,0048 |
1,8070 |
0,5991 |
221,05 |
-1,0884 |
4,6 |
14,669 |
-0,0808 |
1,8933 |
0,5772 |
7,6160 |
-1,1861 |
4,7 |
7,8185 |
-0,1646 |
1,9919 |
0,5543 |
0,4553 |
-1,2865 |
4,8 |
5,4020 |
-0,2572 |
2,1056 |
0,5304 |
-2,2777 |
-1,3895 |
4,9 |
4,1463 |
-0,3612 |
2,2377 |
0,5054 |
-3,8570 |
-1,4954 |
5,0 |
3,3615 |
-0,4772 |
2,3924 |
0,4793 |
-4,9718 |
-1,6040 |
5,1 |
2,8130 |
-0,6100 |
2,5757 |
0,4520 |
-5,8570 |
-1,7155 |
5,2 |
2,3986 |
-0,7630 |
2,7961 |
0,4234 |
-6,6147 |
-1,8299 |
5,3 |
2,0668 |
-0,9423 |
3,0648 |
0,3935 |
-7,2965 |
-1,9473 |
5,4 |
1,7884 |
-1,1563 |
3,3989 |
0,3621 |
-7,9316 |
-2,0679 |
5,5 |
1,5455 |
-1,4181 |
3,8234 |
0,3291 |
-8,5379 |
-2,1917 |
5,6 |
1,3265 |
-1,7481 |
4,3794 |
0,2944 |
-9,1268 |
-2,3189 |
Окончание прил. 13
|
|
|
|
|
|
|
5,7 |
1,1235 |
-2,180 |
5,1346 |
0,2580 |
-9,7056 |
-2,4495 |
5,8 |
0,9302 |
-2,7777 |
6,2140 |
0,2195 |
-10,283 |
-2,5838 |
5,9 |
0,7421 |
-3,6678 |
7,8726 |
0,1790 |
-10,863 |
-2,7218 |
6,0 |
0,5551 |
-5,1589 |
10,727 |
0,1361 |
-11,445 |
-2,8639 |
6,1 |
0,3659 |
-8,2355 |
16,739 |
0,0906 |
-12,038 |
-3,0102 |
6,2 |
0,1700 |
-18,591 |
37,308 |
0,0424 |
-12,643 |
-3,1609 |
2 |
0,0000 |
|
|
0,0000 |
-13,033 |
-3,2898 |
Приложение 14
Таблица значений специальных функций метода
перемещений для сжато-изогнутых стержней
|
|
|
|
|
|
|
0,0 |
1,0000 |
1,0000 |
0,0000 |
1,00000 |
0,00000 |
0,00000 |
0,1 |
0,9967 |
1,0017 |
0,0100 |
0,99500 |
0,09983 |
0,10033 |
0,2 |
0,9866 |
1,0067 |
0,0405 |
0,98007 |
0,19867 |
0,20271 |
0,3 |
0,9698 |
1,0152 |
0,0928 |
0,95534 |
0,29552 |
0,30934 |
04 |
0,9461 |
1,0272 |
0,1691 |
0,92106 |
0,38942 |
0,42279 |
0,5 |
0,9152 |
1,0429 |
0,2731 |
0,87758 |
0,47943 |
0,54630 |
0,6 |
0,8770 |
1,0626 |
0,4105 |
0,82534 |
0,56464 |
0,68414 |
0,7 |
0,8311 |
1,0866 |
0,5896 |
0,76484 |
0,64422 |
0,84229 |
0,8 |
0,7770 |
1,1152 |
0,8237 |
0,69671 |
0,71736 |
1,02964 |
0,9 |
0,7142 |
1,1489 |
1,1341 |
0,62161 |
0,78333 |
1,26016 |
1,0 |
0,6421 |
1,1885 |
1,5574 |
0,54030 |
0,84147 |
1,55741 |
1,1 |
0,5599 |
1,2343 |
2,1612 |
0,45360 |
0,89121 |
1,96476 |
1,2 |
0,4665 |
1,2875 |
3,0866 |
0,36236 |
0,93204 |
2,57215 |
1,3 |
0,3609 |
1,3493 |
4,6827 |
0,26750 |
0,96356 |
3,60210 |
1,4 |
0,2415 |
1,4207 |
8,1170 |
0,16997 |
0,98545 |
5,79788 |
1,5 |
0,1064 |
1,5038 |
21,1521 |
0,07074 |
0,99749 |
14,10142 |
1,6 |
-0,0467 |
1,6007 |
-54,7721 |
-0,02920 |
0,99957 |
-37,23253 |
1,7 |
-0,2209 |
1,7143 |
-13,0842 |
-0,12884 |
0,99166 |
-7,69660 |
1,8 |
-0,4199 |
1,8483 |
-7,7153 |
0,22720 |
0,92385 |
-4,28626 |
1,9 |
-0,6491 |
2,0078 |
-5,5615 |
-0,32329 |
0,94630 |
-2,92710 |
2,0 |
-0,9153 |
2,1995 |
-4,3701 |
-0,41615 |
0,90930 |
-2,18504 |
2,1 |
-1,2282 |
2,4328 |
-3,5907 |
-0,50485 |
0,86321 |
-1,70985 |
2,2 |
-1,6014 |
2,7211 |
-3,0224 |
-0,58850 |
0,80850 |
-1,37382 |
2,3 |
-2,0550 |
3,0843 |
-2,5742 |
-0,66628 |
0,74571 |
-0,11921 |
Продолжение прил. 14
|
|
|
|
|
|
|
2,4 |
-2,6201 |
3,5531 |
-2,1984 |
-0,73739 |
0,67546 |
-0,91601 |
2,5 |
-3,3466 |
4,1773 |
-1,8675 |
-0,80114 |
0,59847 |
-0,74702 |
2,6 |
-4,3218 |
5,0436 |
-1,5642 |
-0,85689 |
0,51550 |
-0,60160 |
2,7 |
-5,711 |
6,3176 |
-1,2764 |
-0,90407 |
0,42738 |
-0,47273 |
2,8 |
-7,8756 |
8,3585 |
-0,9955 |
-0,94222 |
0,33499 |
-0,35553 |
2,9 |
-11,769 |
12,1212 |
-0,7146 |
-0,97096 |
0,23925 |
-0,24641 |
3,0 |
-21,0452 |
21,2585 |
-0,4276 |
-0,98999 |
0,14112 |
-0,14255 |
3,1 |
74,4888 |
74,5533 |
-0,1321 |
-0,99914 |
0,04158 |
-0,04162 |
3,2 |
54,7289 |
-54,8227 |
0,1871 |
-0,99829 |
-0,05837 |
0,05847 |
3,3 |
20,6573 |
-20,9192 |
0,5272 |
-0,98748 |
-0,15775 |
0,15975 |
3,4 |
12,8632 |
-13,3052 |
0,8967 |
-0,96680 |
-0,25554 |
0,26432 |
3,5 |
9,3435 |
-9,9778 |
1,3111 |
-0,93646 |
-0,35078 |
0,37459 |
3,6 |
7,2953 |
-8,1352 |
1,7765 |
-0,89676 |
-0,44252 |
0,49347 |
3,7 |
5,9226 |
-6,9832 |
2,3115 |
-0,84810 |
-0,52984 |
0,62473 |
3,8 |
4,9123 |
-6,2106 |
2,9395 |
-0,79097 |
-0,61186 |
0,77356 |
3,9 |
4,1164 |
-5,6705 |
3,69449 |
-0,72593 |
-0,68777 |
0,94742 |
4,0 |
3,4548 |
-5,2854 |
4,6313 |
-0,65364 |
-0,75680 |
1,15782 |
4,1 |
2,8802 |
-5,0105 |
5,8365 |
-0,57482 |
-0,81828 |
1,42353 |
4,2 |
2,3625 |
-4,8188 |
7,4667 |
-0,49026 |
-0,82158 |
1,77778 |
4,3 |
1,8811 |
-4,6934 |
9,8291 |
-0,40080 |
-0,91617 |
2,28585 |
4,4 |
1,4210 |
-4,6238 |
13,6238 |
-0,30733 |
-0,95160 |
3,09632 |
4,5 |
0,9704 |
-4,6034 |
20,8680 |
-0,21080 |
-0,97753 |
4,63733 |
4,6 |
0,5192 |
-4,6292 |
40,7568 |
-0,11215 |
-0,99369 |
8,86017 |
4,7 |
0,0582 |
-4,7004 |
379,350 |
-0,01239 |
-0,99992 |
80,71276 |
Окончание прил. 14
|
|
|
|
|
|
|
4,8 |
-0,4216 |
-4,8185 |
-54,6474 |
0,08750 |
-0,99616 |
-11,3849 |
4,9 |
-0,9302 |
-4,9875 |
-25,8107 |
0,18651 |
-0,98245 |
-5,26749 |
5,0 |
-1,4791 |
-5,2142 |
-16,9026 |
0,28366 |
-0,95892 |
-3,38052 |
5,1 |
-2,0821 |
-5,5087 |
-12,4919 |
0,37798 |
-0,92581 |
-2,44939 |
5,2 |
-2,7577 |
-5,8860 |
-9,8053 |
0,46852 |
-0,88345 |
-1,88564 |
5,3 |
-3,5303 |
-6,3681 |
-7,9567 |
0,55437 |
-0,63227 |
-1,50127 |
5,4 |
-4,4352 |
-6,9879 |
-6,5747 |
0,63469 |
-0,77276 |
-1,21754 |
5,5 |
-5,5244 |
-7,7954 |
-5,4757 |
0,70867 |
-0,70554 |
-0,99558 |
5,6 |
-6,8801 |
-8,8710 |
-4,5581 |
0,77557 |
-0,63127 |
-0,81394 |
5,7 |
-8,6399 |
-10,3506 |
-3,7605 |
0,83471 |
-0,55069 |
-0,65973 |
5,8 |
-11,0546 |
-12,4839 |
-3,0431 |
0,88552 |
-0,46460 |
-0,52467 |
5,9 |
-14,6362 |
-15,7805 |
-2,3783 |
0,92748 |
-0,37388 |
-0,40311 |
6,0 |
-20,6178 |
-21,4731 |
-1,7461 |
0,96017 |
-0,27942 |
-0,29101 |
6,10 |
- 32,9263 |
-33,4867 |
-1,1301 |
0,98327 |
-0,18216 |
-0,18526 |
6,20 |
-74,3604 |
-74,6184 |
-0,5170 |
0,99654 |
-0,08309 |
-0,08338 |
Приложение 15
Коэффициенты продольного изгиба
λ=l0/i |
Коэффициенты φ для элементов, изготовленных из |
λ=l0/i |
||||
стали, с Ry, МПа |
чугуна |
дюралюминия |
древесины |
|||
200 |
240 |
|||||
10 20 30 40 50 60 70 |
0,988 0,967 0,939 090,6 0,869 0,827 0,782 |
0,987 0,962 0,937 0,894 0,852 0,805 0,754 |
0,97 0,91 0,81 069 0,57 0,44 0,34 |
0,999 0,998 0,835 0,700 0,568 0,455 0,353 |
|
10 20 30 40 50 60 70 |
80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 |
0,734 0,665 0,559 0,537 0,479 0,425 0,376 0,328 0,290 0,259 0,233 0,210 0,191 0,174 0,160 |
0,686 0,612 0,542 0,478 0,419 0,364 0,315 0,276 0,244 0,218 0,196 0,177 0,161 0,147 0,135 |
0,26 0,20 0,16 |
0,269 0,212 0,172 0,142 0,119 0,101 0,087 0,076 |
|
80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 |
Список использованной литературы
1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. /Под ред. А.В. Александрова. – М.: Высшая школа, 2004. – 560 с.
2. Бычков Д.В., Миров М.О. Теоретическая механика. – М.: Высшая школа, 1975. – 240 с.
3. Дарков А.В., Кузнецов В.И. Строительная механика. – М.: Трансжелдориздат, 1956. – 492 с.
4. Дарков А.В., Шпиро Г.С. Сопротивление материалов. – М.: Высшая школа, 1989. – 624 с.
5. Довнар Е.П., Коршун Л.И. Строительная механика. – Мн.: Высшая школа, 1986. – 310 с.
6. Жемочкин Б.Н., Пащевский Д.П. Статика сооружений. Курс строительной механики. Ч.3./Под ред. Проф. Б.Н.Жемочкина – М: Гос. изд. лит. по стр-ву, арх-ре и стр. материалам, 1959. – 339 с.
7. Иванов Г.М., Вейц Р.И. Статика сооружений. – Л.: Изд-во лит. по стр-ву, 1968. – 218 с.
8. Клейн Г.К., Рекач В.Г., Розенблат Г.И. Руководство к практическим занятиям по курсу строительной механики. – М.: Высшая школа, 1972. – 320 с.
9. Копнов В.А., Кривошапко С.Н. Сопротивление материалов. Руководство для решения задач и выполнения лабораторных и расчетно-графических работ. – М.: Высшая школа, 2003. - 351 c.
10. Корчагин В.А., Мисаилов В.Ф., Ульянов В.Д., Якимов С.К. Основы динамики сооружений. – Л.: ЛВВИСКУ, !974. – 206 с.
15. Леонтьев Н.Н., Соболев Д.Н., Амосов А.А. Основы строительной механики стержневых систем. – М.: изд – во АСВ, 1996. – 541 с.
16. Масленников А.М. Начальный курс строительной механики стержневых систем.- СПб.: СПб гос. архит.-строит. ун-т, 1997. – 160 с
17. Масленников А.М. Основы динамики и устойчивости стержневых систем. – М.: изд-во АСВ, 2000. – 204 с.
18. Мухин Н.В., Першин А.Н., Шишман Б.А. Статика сооружений. – М.: Высшая школа, 1980. – 343 с.
19. Смирнов В.А., Иванов С.А., Тихонов М.А. Строительная механика – М.: Стройиздат, 1984. – 208 с.
20. Снитко Н.К. Строительная механика.– М.: Высшая школа, 1972. – 487 с.
21. Справочник проектировщика. Расчётно-теоретический. – М.: Стройиздат, 1961. – 1040 с.
22. Справочник проектировщика. Основания, фундаменты и подземные сооружения. – М.: Стройиздат, 1985. – 479 с.
26. Улитин Н.С. Сопротивление материалов. – М.: Высшая школа, 1969. – 279 с.
Оглавление
Глава 11. Совместное действие растяжения (сжатия) с изгибом
11.1. Статически определимые расчётные схемы, работающие в
условиях совместного действия растяжения (сжатия) с
изгибом
11.1.1. Балки и рамы
11.1.2. Трёхшарнирные арки
11.1.3. Комбинированные расчётные схемы
11.2. Напряжения при совместном действии растяжения (сжатия) с
изгибом
Внецентренное сжатие. Понятие о ядре сечения
Глава 12. Основные теоремы строительной механики. Определение
перемещений
12.1. Основные положения
12.2. Работа сил. Потенциальная энергия деформации
12.3. Принцип возможных перемещений
12.4. Основные теоремы строительной механики
12.4.1. Теоремы о взаимности возможных
работ и взаимности возможных перемещений
12.4.2. Теорема о взаимности возможных реакций
12.5. Определение перемещений в статически определимых
расчётных схемах
12.5.1. Перемещения от внешней нагрузки
12.5.2. Перемещения от теплового воздействия
12.5.3. Перемещения от неравномерной осадки опор
и неточности изготовления стержней
Глава 13. Расчёт статически неопределимых систем методом сил
13.1. Свойства статически неопределимых систем. Степень
статической неопределимости
13.2. Идея метода сил. Система канонических уравнений
13.3. Выбор основных систем метода сил.
Общая последовательность расчёта
13.4. Расчёт при наличии начальных деформаций
13.5. Упрощения при расчёте симметричных систем
13.6. Понятие о расчёте пространственных рам
Глава 14. Расчёт статически неопределимых систем методом
перемещений
Общие положения. Степень кинематической
неопределимости
Идея метода перемещений. Система канонических
уравнений и общая последовательность расчёта
14.3. Упрощения при использовании метода перемещений
14.3.1. Использование основной системы без постановки
линейных связей
Учёт симметрии
14.4. Понятие о расчёте пространственных рам
14.5. Принципы определения перемещений в стати
чески неопределимых системах
Глава 15. Основы динамики сооружений
15.1. Общие положения
15.2. Колебания упругих систем с одной степенью свободы
15.2.1. Свободные колебания
15.2.2. Вынужденные колебания при действии
вибрационной нагрузки
15.2.3. Действие ударной нагрузки
15.3. Колебания упругих систем с несколькими степенями
свободы
15.3.1. Свободные колебания
15.3.2. Вынужденные колебания при действии
вибрационной нагрузки
15.3.3. Учёт симметрии в задачах динамики
15.4. Меры защиты от динамических воздействий
Глава 16. Основы устойчивости сооружений
16.1. Основные положения
16.2. Устойчивость центрально сжатых прямолинейных
стержней
16.3. Применение метода перемещений при расчёте
устойчивости плоских рам
16.3.1. Общие принципы использования метода
16.3.2. Упрощения при расчёте рам на устойчивость
16.4. Критические напряжения и пределы применимости
формулы Эйлера
16.5. Практические расчёты на продольный изгиб
Глава 17. Основы расчёта подпорных стен
17.1. Общие положения
17.2. Активное и пассивное давления на подпорную стену
17.3. Эпюры интенсивности давлений
17.4. Проверка устойчивости и прочности подпорных стен
17.5. Понятие о расчёте тонкостенных подпорных стен
Приложения
Приложение 1. Модули упругости и коэффициенты Пуассона
Приложение 2. Расчетные сопротивления проката для стальных конструкций и отливок из серого чугуна
Приложение 3. Расчетные сопротивления бетона, камня и кирпичной кладки
Приложение 4. Расчетные сопротивления для некоторых сортов древесины
Приложение 5. Геометрические характеристики некоторых плоских сечений
Приложение 6. Двутавры горячекатаные (по ГОСТ 8239 – 89)
Приложение 7. Швеллеры горячекатаные (по ГОСТ 8240 – 89)
Приложение 8. Уголки горячекатаные неравнополочные (по ГОСТ 6510 – 86)
Приложение 9. Уголки горячекатаные равнополочные (по ГОСТ 8509 – 93)
Приложение 10. Таблицы реакций в изгибаемых стержнях от единичных смещений связей
Приложение 11. Таблицы реакций в изгибаемых стержнях от внешних воздействий
Приложение 12. Таблицы реакций в сжато-изогнутых стержнях при расчете на устойчивость
Приложение 13. Таблицы значений функций метода перемещений для сжато-изогнутых стержней
Приложение 14. Таблицы значений специальных функций метода перемещений для сжато-изогнутых стержней
Приложение 15. Коэффициенты продольного изгиба
Список использованной литературы





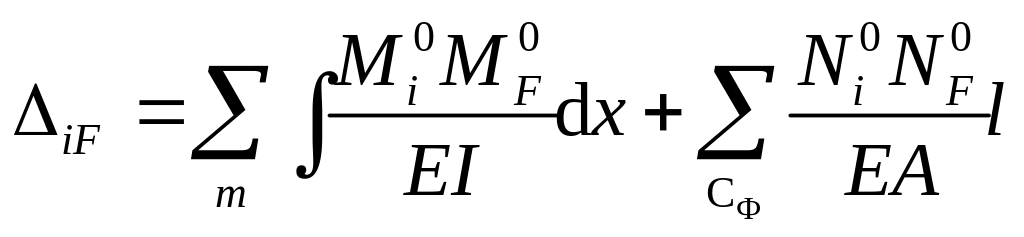

 ,
, ,
, ,
, ,
, ,
, ,
,











