8. 2 Использование принципа Парето

Как уже указывалось, наряду со свертыванием многих показателей к одному, возможны и иные пути к решению задачи многокритериальной оптимизации. Ограничимся обсуждением одного из них, связанного с использованием так называемого принципа Парето.

Сущность данного подхода состоит в исключении из нефор­мального анализа таких вариантов решения, которые заведомо являются плохими. Поясним подробнее данную мысль.

Предположим, что х' и х" — два возможные (допустимые) варианта решения задачи, такие, что имеют место неравенства: f_i(x')≤f_i (х") i=1,m

причем хотя бы одно из них выполняется строго. В этом случае, очевидно, что решение х' предпочтительнее решения х". Значит все векторы х", удовлетворяющие этому условию, могут быть сразу исключены из рассмотрения. Поэтому неформальному ана­лизу должны быть подвергнуты лишь векторы, для которых не существует предпочтительных векторов. Такие векторы называют неулучшаемыми. Множество всех неулучшаемых векторов при­нято называть множеством Парето. Таким образом, множество Парето П состоит из таких векторов х*, для которых из условий f_i(x') ≤f_i (х*) для любого i следует условие

f_i(x') =f_i (х*) .

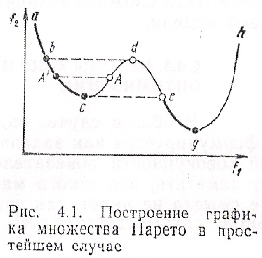
Обратимся к простейшему примеру, когда имеются всего две целевые однозначные функции f1 (х), f2 (х). В этом случае каж­дому значению х будет соответствовать одна точка на плоскости №, (г)- Равенства f1=f1(х), f2=f2 (х) определяют параметрически некоторую кривую а, Ъ, с, d, е, g, h на этой плоскости. Однако множеству Парето соответствует не вся кривая, а лишь ее часть. Действительно, участок сс1 не может принадлежать мно­жеству Парето, так как для каждой точки этого участка А най­дется точка А' участка Ьс, в которой значение целевой функции будет меньше,' чем в точке А. Совершенно аналогично из рас­смотрения должны быть исключены участки dе и gh. К множеству Парето в данном случае относятся лишь участки ас и ед, причем точка е также должна быть исключена.

Таким образом, принцип Парето за­ключается в том, что в качестве опти­мального решения х* должно быть вы­брано только такое, которое принад­лежит множеству Парето, x*эП. Как мы видим, принцип Парето не выделя­ет единственное решение, оно лишь су­жает множество возможных альтернатив. Часто такое сужение оказывается весьма существенным. Окончательный выбор остается за исследователем,

принимающим рекомендации. Если же помимо показателей /;(«), 1=1, т в нашем распоряжении будет некоторый формализованный скалярный показатель для принятия рекомендаций /пр(я), то зада­ча выбора окончательного решении может быть осуществлена из условия:

x* = arg min f_[1Р(x),

где через П обозначено множество Парето для функций /_i (х), i=1, т на допустимом множестве векторов хэХ. Теперь коротко остановимся на вопросе построения множеств Парето. Ограничимся для простоты случаем двух показателей f1(x), f2(x) которые должны быть минимизированы с учетом ограничений xэХ.

Каждой точке хэХ можно поставить в соответствие некоторую точку / с компонентами /^ = /!(*), /а — ^(х), на плоскости пока­зателей . Таким образом, множество X отображается в некоторое множество Р, которое обычно называют множеством достижимости. Множеству Парето П будет соответствовать лишь часть множества достижимости Р. Нетрудно видеть, что в данном случае этой частью является дуга а, Ь.

Обратим внимание на следующую особенность. Любая коор­дината точки дуги а, Ь представляет собой ничто иное как мини­мальное значение одного из показателей при фиксированном зна­чении другого. Поэтому приближенное построение множества Па­рето может быть осуществлено путем последовательного решения ряда задач математического программирования. Одна из возмож­ных схем расчета приведена ниже.

4) Проведя через В¹, В² прямую, получим простейшую аппрок­симацию множества Парето па плоскости показателей.

Для дальнейшего уточнения аппроксимации могут быть най­дены еще две точки В³, В⁴ путем решения дополнительных двух задач оптимизации:

Через точки В¹, Б², В³, В⁴ теперь можно провести ломаную, которая будет следующим кусочно-линейным приближением мно­жества Парето. Процесс уточнения можно продолжить.

Возможны и другие способы приближенного построения множе­ства Парето.