6. Задачи закупочной логистики

Объектом логистики, как известно, является сквозной материальный поток, тем не менее, на отдельных участках управление им имеет свою специфику. В соответствии с этой спецификой выделяют пять функциональных областей логистики: закупочную, производственную, распределительную, транспортную и складскую.

Закупочная логистика управляет процессом обеспечения предприятий материальными ресурсами, размещения ресурсов на складах предприятия, их хранения и выдачи в производство.

Целью логистики закупок является удовлетворение потребностей производства в материалах с максимально возможной экономической эффективностью.

Логистика закупок решает следующие задачи:

- определение потребностей в материальных ресурсах;

- оценка предложений от потенциальных поставщиков и выбор поставщиков;

- согласование цены заказываемых ресурсов и заключение договоров на поставку;

- контроль за сроками поставки материалов;

- входной контроль качества материальных ресурсов и их размещение на складе;

- доведение материальных ресурсов до производственных подразделений;

- поддержание на должном уровне запасов материальных ресурсов на складах.

7. Методы определения потребностей

Необходимым условием эффективного управления материальными потоками является знание потребности на перспективу. Для ее определения могут использоваться следующие методы:

- детерминированные методы расчета в соответствии с планом производства и имеющимися нормативами на выпускаемую продукцию;

- стохастические методы прогнозирования;

- субъективная оценка по заключениям экспертов.

К детерминированным методам расчета потребностей относится метод прямого счета:

, (7.1)

где Р_i – потребность в материале i-го вида;

П_j – план производства j-ой продукции;

Н_ij – норма расхода i-го материала на производство единицы j-го продукта;

m – количество наименований продукции, на производство которой требуется i-ый материал.

Для того, чтобы получить изделия с заранее заданным качеством, разрабатываются рецептуры. В них указываются процентные соотношения каждого материала, который расходуется для производства этих изделий.

В таких случаях первоначально определяется вес готовой продукции в соответствии с производственной программой (Р_гот). Он устанавливается умножением веса одного изделия на производственную программу изготовления изделий.

На втором этапе расчетов устанавливается вес каждого конкретного материале в готовом продукте (Р_готi). Этот вес определяется по формуле

, (7.2)

где К_i –доля (по весу) данного (i-го) материала в общем составе смеси для изготовления изделий по рецепту.

Последним этапом является установление веса материала, который должен быть отпущен в производство с учетом потерь в технологическом процессе (Р_отпi). Расчет производится по формуле:

(7.3)

где К_выхi – коэффициент выхода готовой продукции, учитывающий потери i-го материала на всех стадиях технологического процесса производства изделий.

Задание 2.

1. Рассчитать потребность в материале по данным таблицы

   Ассортимент	Программа производства, пар	Норма расхода материала, дм2	Потребность в материале, дм2
   Сапоги мужские	1400	130
   Полуботинки мужские	1150	30
   Ботинки мужские	50	62
   Сапоги женские	90	105
   Ботинки женские	150	45
   Туфли женские	640	19
   Ботинки детские	90	31
   Полуботинки детские	105	17
   Итого

2. Заводу технического стекла надо изготовить 25 000 штук изделия А и 10 000 штук изделия В при весе одного изделия соответственно 2 кг и 1 кг. Выход готовой продукции для всех материалов– 80 %. Рецептурный состав смеси представлен в таблице.

Наименование материала	Содержание, %
Песок кварцевый	70
Известь	8
Окись натрия	16
Окись магния	4
Окись алюминия и железа	2
Итого	100

Рассчитать потребность в перечисленных материалах

Стохастические методы прогнозирования позволяют оценить ожидаемую потребность на основе временных рядов, характеризующих ее изменение на протяжении определенного промежутка времени. При этом используют прогноз по среднему значению, метод экспоненциального сглаживания и метод экстраполяции временного ряда.

Прогноз по среднему значению используется в условиях, когда потребность в материалах колеблется по месяцам при устойчивом среднем значении (отсутствие тренда).

Прогнозирование этим методом представляет собой процедуру усреднения известных значений потребности в материалах.

Экспоненциальное сглаживание временного ряда y_t осуществляется по рекуррентной формуле

, (7.4)

где S_t- значение экспоненциальной средней в момент времени t;

a – параметр сглаживания (0<a<1);

=1-a.

Выражение (7.4) можно переписать следующим образом

. (7.5)

В формуле (7.5) экспоненциальная средняя на момент времени t выражена как сумма экспоненциальной средней предшествующего периода S_t-1 и доли a разницы текущего значения временного ряда y_t и экспоненциальной средней S_t-1.

Последовательное применение рекуррентной формулы (7.4) приводит к следующему выражению для S_t

_, (7.6)

где n – число точек временного ряда;

S₀ - некоторая начальная величина, необходимая для первого

применения формулы (7.4).

Из формулы (7.6) видно, что S_t оказывается взвешенной суммой всех уровней временного ряда. При этом веса падают экспоненциально с возрастанием «возраста» данных.

Экспоненциальная средняя S_t может быть использована не только для сглаживания временного ряда, но и для краткосрочного прогнозирования.

Прогнозная модель имеет вид

, (7.7)

где - прогноз, сделанный в момент времени t на  единиц времени вперед.

Отметим, что все свойства экспоненциальной средней распространяются на прогнозную модель. В частности, если S_t-1 рассматривать как прогноз на 1 шаг вперед в момент времени t-1, то величина y_t-S_t-1 представляет собой погрешность этого прогноза, а новый прогноз S_t получается в результате корректировки предыдущего прогноза с учетом его ошибки по формуле (7.5). В этом и состоит суть адаптации.

При краткосрочном прогнозировании желательно с одной стороны быстро отразить изменение среднего уровня, а с другой – очистить ряд от случайных колебаний.

Для выполнения первого требования величину a следует увеличить, а для выполнения второго – уменьшить. Таким образом, эти два требования находятся в противоречии и необходим некий компромисс.

Рассмотрим вопрос выбора параметра a. При S_t= S₀, т.е. адаптация полностью отсутствует, а при имеет место так называемая «наивная» модель прогнозирования

,

в соответствии с которой прогноз на любой срок равен текущему (последнему) значению временного ряда. В ряде работ рекомендовано брать значение a в пределах от 0,1 до 0,3, однако эта рекомендация по сути не имеет должного обоснования.

Выбор начального значения S₀ всегда вызывает вопрос, однако величина быстро убывает с ростом i и влияние S₀ на величину S_t становится несущественным.

Пример.

Для иллюстрации процедуры расчета экспоненциальной средней рассмотрим пример сглаживания динамики курса акций фирмы IBM, производящей ЭВМ (табл. 4).

Т а б л и ц а 4. Экспоненциальные средние

Номер точки	Исход-ный ряд				Номер точки	Исход-ный ряд
1	510	506,4	508,0	509,6	16	512	505,7	513,3	513,1
2	497	505,5	502,5	498,3	17	510	506,1	511,7	510,3
3	504	505,3	503,2	503,4	18	506	506,1	508,8	506,4
4	510	505,8	506,6	509,3	19	515	507,0	511,9	514,1
5	509	506,1	507,8	509,0	20	522	508,5	517,0	521,2
6	503	505,8	505,4	503,6	21	523	509,9	520,0	522,8
7	500	505,2	502,7	500,4	22	527	511,6	523,5	526,6
8	500	504,7	501,4	500,0	23	523	512,8	523,2	523,4
9	500	504,2	500,7	500,0	24	528	514,3	525,6	527,5
10	495	503,3	497,8	495,5	25	529	515,8	527,3	528,9
11	494	502,4	495,9	494,2	26	538	518,0	532,7	537,1
12	499	502,0	497,5	498,5	27	539	520,1	525,8	538,8
13	502	502,0	499,7	501,2	28	541	522,2	538,4	540,8
14	509	502,7	504,4	508,3	29	543	524,3	540,7	542,8
15	525	505,0	514,7	523,3	30	541	525,9	540,9	541,2

При проведении расчетов начальное значение экспоненциальной средней S₀ было принято равным средней арифметической из первых 5 уровней ряда

В нашем случае

Дальнейшие вычисления при выглядят следующим образом

и т. д.

Результаты вычислений экспоненциальных средних при a=0,1, a=0,5 и a=0,9 приведены в табл. 4.

Суть метода экстраполяции временного ряда состоит в распространении существующих закономерностей (тенденций и связей) на некоторый период в будущем. Динамическая (временная) экстраполяция основывается на предположении, что имеющийся временной ряд y_t представляет собой сумму двух составляющих – регулярной и случайной.

y _t = f (t) +  _t , (7.8)

где f (t) - регулярная составляющая;

 _t- случайная величина с нулевым математическим ожиданием.

В основе экстраполяционного метода лежит интуитивное представление о какой-то очищенной от помех сущности анализируемого процесса. Применение этого метода фактически сводится к построению наилучшего в некотором смысле описания регулярной составляющей и экстраполяции его на прогнозный момент времени.

Выбор типа функции f (t) осуществляется на основании визуального анализа динамики показателя. В качестве функций обычно используются:

- линейная f (t) = a₀ + a₁ t (7.9)

- полиномиальная f (t) = a₀ + a₁ t + a₂ t² + .... + a_n tⁿ ; (7.10)

bt

- экспоненциальная f (t) = a e ; (7.11)

a

- логистическая кривая f(t) = --------------------- (7.12)

-ct

1 + b e

и другие простые математические зависимости.

Методы экстраполяции целесообразно использовать при прогнозировании показателей в тех случаях, когда имеется достаточно представительная статистика, позволяющая провести построение временных рядов, причем прогнозируемые события должны носить массовый характер.

Методы экспертного прогнозирования используют индивидуальные или групповые мнения о перспективах развития прогнозируемого объекта и могут использоваться при отсутствии или сложности получения статистической информации.

Индивидуальные экспертные оценки основаны на использовании мнений экспертов, полученных независимо друг от друга. Напротив, методы коллективных экспертных оценок, например, "мозговой атаки" (коллективной генерации идей) основываются на всестороннем обсуждении ситуации членами группы. Промежуточное положение занимают анкетные методы с обратной связью, такие как "Дельфи". Достоинством этой группы методов является наличие влияния мнений одних экспертов на других за счет переосмысливания первоначальных суждений на основе анализа высказываний других экспертов.

Комбинированная прогнозная оценка

Каждый из методов прогнозирования имеет свои преимущества и недостатки по сравнению с другими методами. Поэтому можно говорить о возможности и необходимости комбинированного прогноза. Для получения комбинированной прогнозной оценки необходимо решить две задачи:

- установить область, внутри которой прогнозные результаты, полученные разными методами, можно считать непротиворечивыми;

- получить аналитическое выражение для комбинированной прогнозной оценки.

В комбинированной оценке может участвовать несколько прогнозов , полученных разными методами, если эти прогнозы не противоречат друг другу. В противном случае необходим анализ причин противоречивости результатов, исключение некоторых вариантов прогнозов, повторное прогнозирование, анализ и проверка исходных данных.

Совместная обработка прогнозов заключается в определении средневзвешенного результата прогнозов, полученных различными методами с учетом их точности. Чем менее точен результат, тем меньше его вес в окончательном прогнозе. Для получения прогнозов с минимальной дисперсией весовые коэффициенты рассчитываются по формуле

(7.13)

где N – количество прогнозов, участвующих в комбинированной оценке;

- дисперсия i-го прогноза.

После преобразования формулы (7.13) для двух прогнозов получим следующую зависимость для расчета весовых коэффициентов

и

Комбинированная прогнозная оценка определяется по формуле

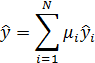
(7.14)

При этом дисперсия комбинированного прогноза равна

(7.15)

Задание 3.

1. Сделайте прогноз потребности в материалах на следующий месяц методом экспоненциального сглаживания, если прогноз на текущий месяц составил 650 единиц, однако фактически потребовалось только 550. Параметр сглаживания α равен 0,3.

2. Прогнозы, полученные методом экстраполяции и экспертным методом составили соответственно 560 и 580 единиц продукции, средняя квадратическая ошибка этих прогнозов соответственно 35 и 45 единиц. Построить комбинированный прогноз и найти его дисперсию.