8) Проверка вывода пункта 5 с помощью частотного критерия Михайлова.

Характеристический полином системы:

A(s)=0.0735s⁴+0.6265s³+4.97998s²+23.05s+30;

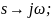
Вещественная функция Михайлова:

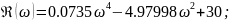
Мнимая функция Михайлова:

Для построения годографа Михайлова решаем уравнения:

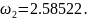
Таблица 5

	0	2.58522	6.06562	7.81484
	30	0	-53.7302	0
	0	48.76468	0	-118.8749

Замкнутая САУ будет устойчивой тогда и только тогда, когда годограф Михайлова, при изменении  от 0 до +∞, начинаясь на положительной действительной полуоси последовательно и нигде не обращаясь в 0, пересекает 4 квадрата комплексной плоскости. Приведенный на рисунке график соответствует критерию Михайлова, следовательно, замкнутая САУ устойчива.

9) Нахождение коэффициентов c0, c1, c2 ошибок системы.

Передаточная функция ошибки имеет вид:

Коэффициенты ошибок системы равны:

10) Построение с помощью эвм переходной функции замкнутой системы и оценивание основных показателей качества регулирования (перерегулирование и время регулирования) в системе.

Переходная функция замкнутой системы:

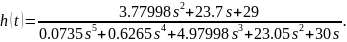
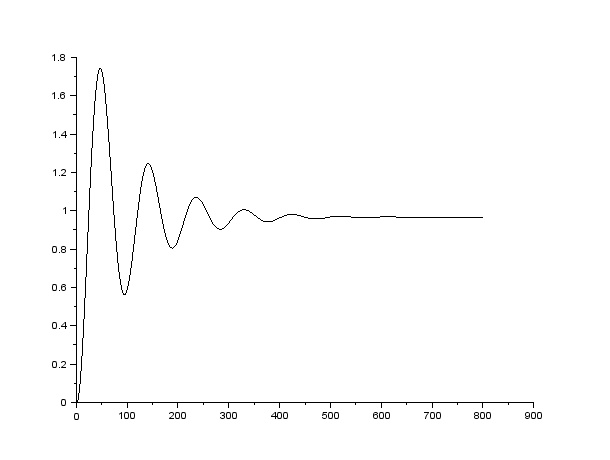
Рисунок 11 – переходная функция

Время регулирования составляет:

Перерегулирование равно:

Список использованной литературы

1. Анализ линейных систем автоматического управления: Методические указания к выполнению курсовой работы по дисциплине “Теория автоматического управления” / Уфимск. гос. авиац. техн. ун-т; Сост. Ф. М. Ахмеджанов, В. Г. Крымский. – Уфа, 2009. – 41с.

2. Теория систем автоматического управления / В. А. Бесекерский, Е. П. Попов. – Изд. 4-е, перераб. и доп. – СПб, Изд-во “Профессия”, 2003. – 752 с.

Действия, выполненные в Scilab для решения задач курсовой работы

3) s=poly(0,'s');

a=3.14998*s^2+20.8*s+29;

b=0.0735*s^4+0.6265*s^3+1.83*s^2+2.25*s+1;

w=syslin('c',a/b);

nyquist(w,0,100)

4) s=poly(0,'s');

a=3.14998*s^2+20.8*s+29;

b=0.0735*s^4+0.6265*s^3+1.83*s^2+2.25*s+1;

w=syslin('c',a/b);

bode(w,0.001,100)

6) s=poly(0,'s');

a=3.14998*s^2+20.8*s+29;

b=0.0735*s^4+0.6265*s^3+1.83*s^2+2.25*s+1;

w=syslin('c',a/b);

p_margin(w)

10) s=poly(0,'s');

a=3.77998*s^2+23.7*s+29;

b=0.0735*s^4+0.6265*s^3+4.97998*s^2+23.05*s+30;

w=syslin('c',a/b);

t=0:0.01:20;

csim('step',t,w);

plot2d(csim('step',t,w))