Содержание

Введение 2

Задание на проектирование и порядок выполнения работы 3

Исходные данные 4

Ход выполнения работы 5

1) Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы. 5

2) Определение амплитудно-фазовой, вещественной и мнимой частотных характеристик разомкнутой системы. 9

4) Нахождение выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы. Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы. 11

5) Определение устойчивости замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик. 12

6) Нахождение запасов устойчивости системы по фазе и по амплитуде. 13

7) Нахождение передаточной функции замкнутой системы и проверка выводов пункта 5 с помощью алгебраических критериев Рауса и Гурвица. 14

8) Проверка вывода пункта 5 с помощью частотного критерия Михайлова. 17

9) Нахождение коэффициентов C0, C1, C2 ошибок системы. 19

10) Построение с помощью ЭВМ переходной функции замкнутой системы и оценивание основных показателей качества регулирования (перерегулирование и время регулирования) в системе. 20

Список использованной литературы 22

Действия, выполненные в Scilab для решения задач курсовой работы 23

Введение

Целью выполнения курсовой работы является закрепление полученных студентами знаний в области теории линейных систем автоматического управления (САУ) и выработка навыков их самостоятельного теоретического и экспериментального исследования. Основное внимание уделяется изучению динамических характеристик, а также анализу устойчивости и качества переходных процессов в этих системах. Тематика курсовой работы соответствует утвержденной учебной программе дисциплины «Теория автоматического управления» и охватывает ее основные разделы.

Курсовая работа выполняется студентом самостоятельно. Задание необходимо получить от преподавателя на 3-4 неделе, после того, как на лекциях будет получен определенный теоретический задел для начала выполнения работы. Студент должны четко представлять себе цель и содержание каждого раздела работы и ожидаемые результаты. Выполнение каждого раздела верифицируется на консультациях с преподавателем.

На защиту каждой курсовой работы студентом представляется отчет о ее выполнении, подготовленный в соответствии с требованиями, которые приводятся в настоящем учебно-методическом пособии.

Моделирование и анализ исследуемых систем осуществляются на базе специализированного программного пакета SciLab, предоставляемого пользователям в режиме свободного доступа в дисплейных классах кафедры.

Задание на проектирование и порядок выполнения работы

1)Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы.

2)Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики разомкнутой системы.

3)Построить годограф АФХ разомкнутой системы.

4)Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы. Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы.

5)Определить устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик.

6)Найти запасы устойчивости системы по фазе и по амплитуде.

7)Найти передаточную функцию замкнутой системы и проверить выводы пункта 5 с помощью алгебраических критериев Рауса и Гурвица.

8)Проверить выводы пункта 5 с помощью частотного критерия Михайлова.

9)Найти коэффициенты C0, C1, C2 ошибок системы.

10)Построить с помощью ЭВМ переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование и время регулирования) в системе.

Исходные данные

Таблица 1

№	Схема	k1	k2	k3	k4	k5	T1	T2	T3	T4
22	d	0.9	2	2	20	2	0.7	0.7	0.5	0.6

Структурная схема САУ

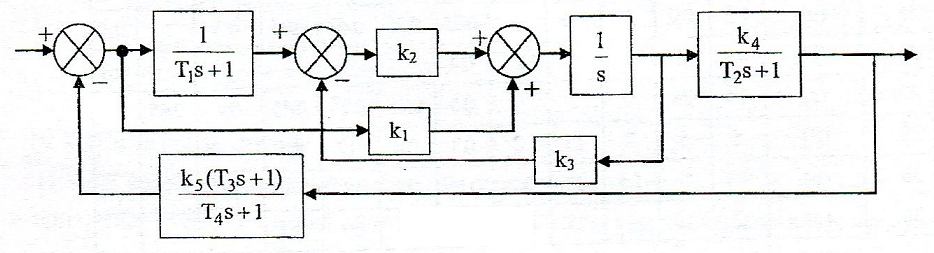
Рисунок 1 – схема d

Ход выполнения работы

1) Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы.

Рисунок 2 – исходная схема d

Для начала упростим исходную схему САУ, применив правило переноса сумматора. Перенесём 3-ий сумматор назад через звено с передаточной функцией k₂. При этом следует в линию связи по второму входу сумматора включить элемент с передаточной функцией 1/k₂ обратного звена (рисунок 3).

Рисунок 3 – перенос сумматора

Затем нужно поменять местами два сумматора по правилу перестановки сумматоров. Также два последовательно соединенных звена с передаточными функциями k₁ и 1/k₂ представим в виде звена с передаточной функцией k₁/k₂, т.е. , а последовательно соединённые звенья с передаточными функциям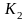и и в виде звена с передаточной функцией (рисунок 4).

Рисунок 4 - замена местами сумматоров

Подставим исходные данные в схему (рисунок 5).

Рисунок 5 – схема с подставленными данными

В результате получается схема, состоящая из 6 звеньев со следующими передаточными функциями:

;

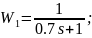
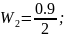
При этом звенья 1 и 2 параллельны, а звено 3 охвачено локальной обратной связью со звеном 4 в цепи ОС. Найдем эквивалентные передаточные функции:

;

;

Рисунок 6 – упрощенная схема d

Передаточная функция прямой цепи:

.

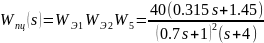Передаточная функция разомкнутой цепи:

.

Порядок астатизма .

Коэффициент передачи K=29.

Постоянные времени:

T₁=0.21724; T₂=0.5 – в числителе;

T₃=0.7; T₄=0.7; T₅=0.25; T₆=0.6 – в знаменателе.