4.2 Теплоємність газів при постійному тиску і постійному об'ємі

Повною теплоємністю системи (або просто її теплоємністю) називають фізичну величину, чисельно рівну теплоті, необхідній для нагрівання системи на один кельвін

(5)

При різних процесах теплоємність приймає різні значення. Звичайно виділяють теплоємність при постійному тиску Cp і при постійному об'ємі Cv. Використовуючи вирази для теплоти при ізобаричному і ізохоричному процесах, легко отримати:

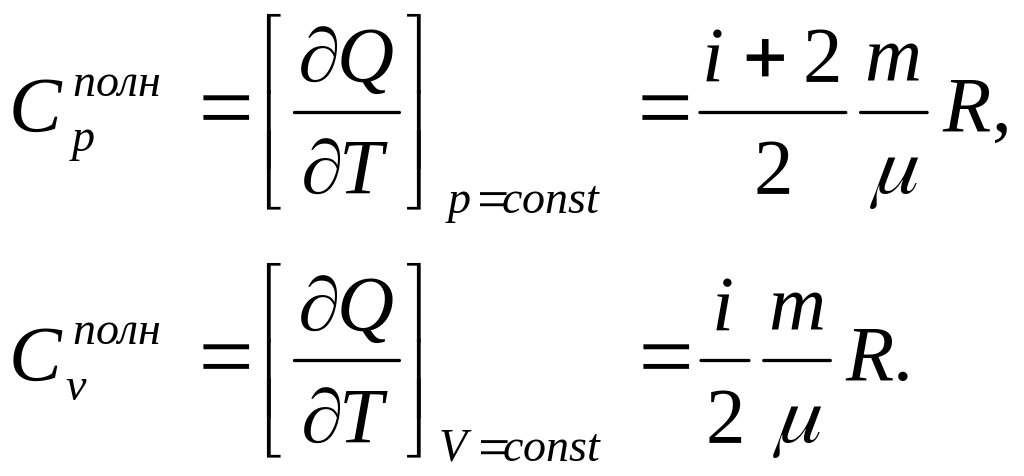
Розрізняють питому і молярну теплоємності.

Питома теплоємність - теплоємність, що доводиться на одиницю маси системи:

Молярна теплоємність - теплоємність, що доводиться на один моль речовини:

З отриманих формул витікає, що

C_p = C_V + R. (6)

Це співвідношення називають рівнянням Майєра.

Відношення теплоємності при постійному тиску до теплоємності при постійному об'ємі рівне

(7)

4.3 Адіабатний (адіабатичний) процес

Газовий процес, який відбувається без теплообміну між газом і навколишнім середовищем, називається адіабатним процесом.

Практично адіабатний процес здійснюється при достатньо швидкому розширенні або стисненні газу, коли теплообмін між газом і середовищем не встигає відбутися. Зв'язок між параметрами стану ідеального газу при адіабатному процесі (тут і далі будемо розглядати врівноважені процеси) виражається рівнянням Пуассона:

(8)

де Тому величину  часто називають показником адіабати.

Користуючись рівнянням Менделєєва-Клапейрона, можна записати рівняння Пуассона в наступній формі:

(9)

Оскільки то із співвідношення (9) слідує, що при адіабатному стисненні газ нагрівається, при адіабатичному розширенні охолоджується.

5. Опис лабораторної установки і методу дослідження

Лабораторна установка складається з балона 1, манометра 2, пробки-клапана і насоса 4 (див. рис.5.1).

Розглянемо метод Клемана-Дезорма, що дозволяє за допомогою установки, зображеної на рис.1.2, визначити . Якщо в посудину 1 за допомогою насоса 4 накачати при закритому клапані 3 повітря, то через деякий час температура повітря в посудині стане рівною кімнатній: T₁ = T₀, тиск р₁ буде вищим атмосферного р₀; р і Т характеризують стан 1 (див.рис.5.2).

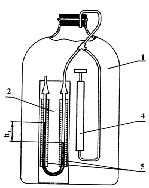
Рисунок 5.1- Схема експериментальної установки: 1 - балон; 2 - манометр; 3 пробка- клапан; 4 - насос; 5 - шкали манометра

Отже

р₁ = р₀ + gh₁, T₁ = T₀ (10)

 - густина рідини манометра; h₁ - перепад рівнів рідини у манометрі (див.рис.5.1). Якщо потім відкрити пробку-клапан 3 і закрити її знову у той момент, коли тиск у посудині стане рівним атмосферному (зробити це треба достатньо швидко), то відбудеться адіабатне розширення газу у посудині. В цьому випадку тиск газу буде рівний атмосферному, тобто р₂=р₀, а температура Т₂ внаслідок адіабатного розширення буде нижче кімнатної (стан 2 на рис.5.2):

р₂ = р₀, T₂ <T₀ .

З часом температура повітря, що залишилося, у закритій судині буде підвищуватися і досягне кімнатної. Тиск підвищиться до значення р₃, об'єм залишиться незмінним, оскільки посудина закрита (стан 3 на рис.2):

р₃ = р₀ + gh, T₃ = T₀ . (11)

Перехід газу із стану 1 в стан 2 відбувається а діабатично і підкоряється рівнянню Пуассона, яке в цьому випадку зручно записати у вигляді

або ж . (12)

P

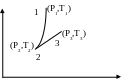
0

T

Рисунок 5.2 - PТ - діаграма процесів, що відбуваються в експериментальній установці

Із стану 2 в стан 3 газ переходить ізохорично:

або ж . (13)

Виключаючи з (12) і (13) температуру, знайдемо

(14)

Підставляючи (10) і (11) в рівняння (14), отримаємо

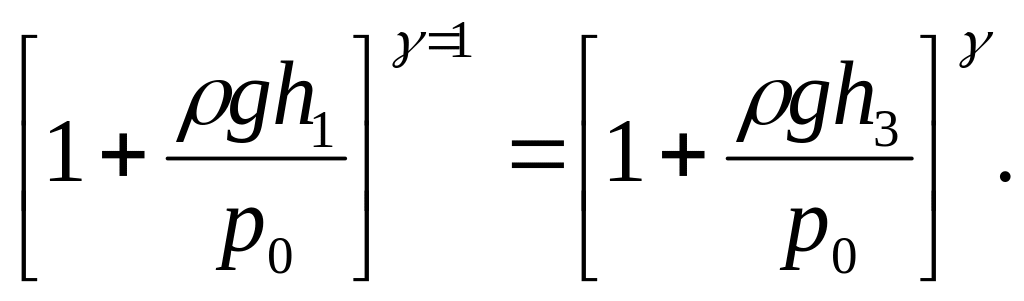
Оскільки і, то можна скористатися наближеним співвідношенням (1 + ⁿ  1 + n .

Тоді

Звідси отримаємо розрахункову формулу

(15)

Таким чином, виміряючи h₁, h₃ і використовуючи (15), можна визначити відношення теплоємкостей