Построение вариационного ряда для точечной оценки параметра мерного признака

Xmax=47

Xmin= 7

Кх=8

Таблица 2

Ymax=105

Ymin=10

Ky=19

Таблица 3

Полигон х

Вершина кривой сдвинута к началу графика, следовательно, распределение по Пуассону.

Полигон у

Вершина кривой сдвинута к началу графика, следовательно, распределение по Пуассону.

r< 50%, корреляция слабая

Вывод: в результате исследования мы получили, что собранный нами материал средней однородности, а корреляция признаков оказалась слабой, из этого следует, что варьирование обоих признаков происходит практически не зависимостью друг от друга ( т.е. количество листьев не зависит от высоты стебля).

Полиморфизм природных популяций

Популяция – совокупность особей данного вида, характеризующаяся общностью происхождения, общностью местообитания и образующая целостную генетическую систему, относительно изолированную от других совокупностей того же вида. Популяция – элементарная единица эволюции.

Полиморфизм – устойчивое присутствие в популяции как минимум двух морфологических форм, при этом условно принято, что частота самой редкой не должна быть менее 1%. Полиморфизм является обычным состоянием природных популяций.

Занятие 2. Полиморфизм рисунка на листьях клевера Trifolium repens

Цель: описать фенотипическое разнообразие белого клевера по окраске листьев и сравнение двух популяций по частоте встречаемости разных фенотипов.

Задание: собрать листья из двух популяций белого клевера.

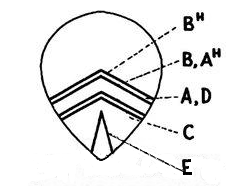
Рис.1 Уровни расположения пятен различного типа

Ход выполнения: нами была осуществлена выборка с 50 растений, расположенных друг от друга на расстоянии не менее 2 метров, по 1 среднему листу. Все собранные листья были одного размера. Одна популяция клевера была собрана с ул. Шмидта, другая с Долины Уюты.

Затем с использованием статистических методов две эти популяции сравнили по частоте встречаемости растений без пятна. Используя формулу Харди-Вайнберга, вычислили частоту рецессивной аллели в этих популяциях.

Биологический материал прилагается.

Данные, необходимые для расчёта частоты рецессивной аллели в этих популяциях

Серия множественных аллелей в локусе V у Trifolium repens

Закон Харди-Вайнберга - показывает частоту встречаемости рецессивного гена (p+q)²=1

Наличие пятна – ген в доминантном состоянии (А)

Отсутствие пятна – ген в рецессивном состоянии (а)

Частота встречаемости гена в доминантном состоянии (А) = р

Частота встречаемости гена в рецессивном состоянии (а) = q

Сумма частот доминантных и рецессивных аллелей одного гена равна 1 или 100%.

p+q=1,т.к. частота встречаемости АА,2Аа,аа.

p²AA+2pqAa+q²aa=1

AA,Aa-82%

aa-18%

Частота встречаемости аллеля А= p; a=1-p

Решив систему, находим значение k и подставляем в формулу Харди-Вайнберга.

p² +2 p(1-p)=0,82

(1-p)² =0,18

1)p²+2p-2q²=0,82

p²-2p-0,82=0

p₁=2,3

2) 1-2p+ p²=0,18

p²-2p+0,82=0

p₂=1,4

p₃=0,6

1 участок

A= 47 (виды с пятном – доминантный признак)

a = 3 (виды без пятна – рецессивный)

A = q

a = 1 – q

q²_{AA +} 2q (1 – q)_Aa +(1 – q)²_aa = 1

Закон Харди-Вайнберга (p + q)² = 1 - показывает частоту встречаемости рецессивного гена

q² + 2q (1 – q) = 0,47

(1 – q)² = 0,03

1. q² + 2q (1 – q) = 0,47

2q - q² – 0,47 = 0

q² – 2q + 0,47 = 0

D = (-2)² – 4*0,47 = 4 – 1,88 = 2,12 ~ (1,46)²

→ x₁= 2 + 1,46/2 = 1,73

x₂= 2 – 1,46/2 = 0,27

2. (1 - q²) = 0,03

1 – 2q + q² = 0,03

q² – 2q + 0,07 = 0

D = (-2)² – 40,07 = 4 – 0,28 = 3,72 ~ (1,93)²

→ x₁ = (2 + 1,93) /2 = 1,96

x₂ = (2 – 1,93) /2 = 0,03

2 участок

A = 0,35

a = 0,15

q² + 2q (1 – q) = 0,35

(1 – q)² = 0,15

1. q² + 2q - 2 q² = 0,35

q²- 2q + 0,35 = 0

D = (-2)² – 4*0,35 = 4 – 1,4 = 2,6 ~ (1,6)²

→ x₁= (2 + 1,6) /2 = 1,8

x₂ = (2 – 1,6) /2 = 0,2

2. 1 – 2q + q²= 0,15

q²–2q + 0,85 = 0

D = (-2)² – 4*0,85 = 4 – 3,4 = 0,6 ~ 0,8

→ x₁ = (2 + 0,8) / 2 = 1,4

x₂ = (2 – 0,8) / 2 = 0,6

Вывод: в ходе данного исследования были изучены 4 аллели гена. И таким образом было выявлено, что на ул. Шмидта фенотипическое разнообразие клевера больше, чем в Долине уюта. А частота рецессивной аллели на территории Долины уюта значительно выше.