
- •1. Принцип Гюйгенса.
- •2. Гауссов пучок.
- •3. Лазерные пучки высшего порядка.
- •4. Комплексный параметр Гауссова пучка.
- •5. Алгоритм расчета системы (гауссов пучок).
- •2. Введение в теорию лазерных резонаторов.
- •3. Алгебра резонатора
- •4. Частотный спектр лазерного резонатора.
- •2. Перестройка частотного спектра резонатора.
- •5. Добротность резонатора
- •6. Критерий малости дифракционных потерь.
- •7. Элементы дифракционной теории лазерных резонаторов.
- •8. Метод эквивалентного конфокального параметра.
- •3. Основы поляризационной теории лазерных пучков.
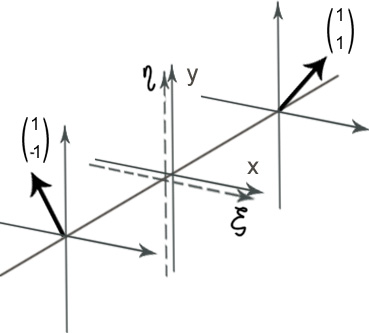
- •1. Линейная поляризация.
- •3. Эллиптическая поляризация.
- •4. Диаграмма Пуанкаре.
- •5. Основные свойства поляризационных векторов и описываемых ими состояний поляризации лазерного луча.
- •3. Физический смысл ортогональности поляризации.
- •6. Матричное описание поляризационно-анизотропных оптических элементов
- •7. Фазовые платинки как поляризационно-анизотропные оптические элементы.
- •2. Вращающаяся четвертьволновая пластинка.
- •11. Электрооптический амплитудный модулятор.
- •12. Поляризационный эффект Фарадея.
- •2) Эффект Фарадея.
- •3) Применение эффекта Фарадея.
- •4.Поляризационные методы расчета лазерных резонаторов.
- •1. Собственные поляризации резонатора.
- •2. Физический смысл модуля и аргумента
- •3. Пример.
- •2. Одночастотная генерация.
- •5. Методы селекции частот и мод в лазерных резонаторах.
- •1. Селекция переходов (выделение требуемой длины волны)
- •2. Фильтры.
- •3. Дисперсионные элементы в резонаторе как элементы селекции длин волн.
- •4. Дифракционная решетка в резонаторе для селекции длин волн.
- •1. Селекция поперечных типов колебаний в лазерных резонаторах.
- •2. Использование призм полного внутреннего отражения (пво) для селекции поперечных мод.
- •3. Методы селекции частот (продольных типов колебаний)
- •1. Поляризационно-частотные методы селекции.
- •2. Селекция частоты в лазерах с однородным контуром усиления.
- •3. Применение внутрирезонаторных многолучевых интерферометров для селекции частот.
- •3. Методы стабилизации частоты лазерного излучения.
- •1. E(t) – поле в резонаторе.
- •2. P(t) - поляризация.
- •3. Δn(t) – инверсия населенностей.
- •2. Режим нестационарной генерации.
- •3. Режим модуляции добротности.
- •4. Режим синхронизации мод.
- •1. Уравнения для электромагнитных колебаний.
- •2. Уравнения для поляризации и инверсии населенностей.
- •1. Основные положения квантовой механики.
- •2. Дипольный момент.
- •4. Эрмитовы операторы:
- •6. Значение дипольного момента:
- •7. Инверсия.
- •8. Поляризация.
- •3. Усиление световой волны в активной среде.
- •1. Проведем анализ уравнения (1)
- •2. Проведем анализ уравнения (2)
- •3. Проведем анализ уравнения (3)
- •4. Рассмотрим уравнение инверсии для стационарного случая.
- •5. Нестационарный режим генерации (динамический режим) в резонаторе.
- •6. Приведение трехуровневой системы к двухуровневой.
3. Физический смысл ортогональности поляризации.
Ортогональные поляризации не интерферируют- одна волна не может погасить другую (подбором сдвига фаз)
При сложении получается световая волна с другой поляризацией (интенсивность остается той же самой)
Интенсивность- определяется скалярным произведением:
![]() ,
где
,
где
![]() - эрмитово сопряжение (
- эрмитово сопряжение (![]() и
и
![]() )
)
6. Матричное описание поляризационно-анизотропных оптических элементов
1. Поляризационно-изотропные элементы не меняют поляризацию. (слой пространства, аморфные материалы с исключением механических напряжений, напряжения электрического поля)
![]()
Поляризационно-изотропный
элемент описывается единичной матрицей:
![]()
2. Поляризационно-анизотропные элементы
Пример
1) поляризационно-анизотропного элемента : зеркало для круговой поляризации.
При нормальном падении луча левокруговая поляризация переходит в правокруговую.
![]()
2)
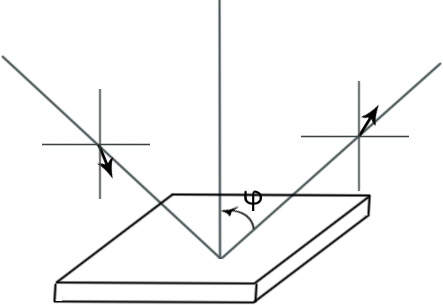
При наклонном падении на диэлектрик имеет место изменение поляризации- деполяризация луча.
На
входе:
![]() ,
на выходе:
,
на выходе:
![]() ,
,
=![]()
Поляризационно-анизотропный элемент.
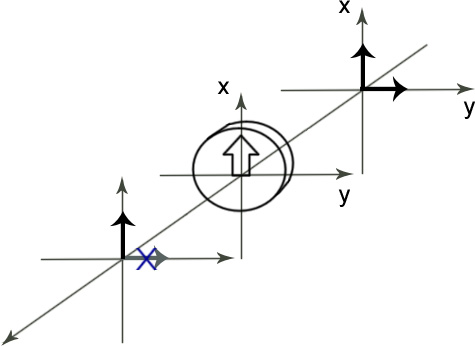
![]() ,
,
![]()
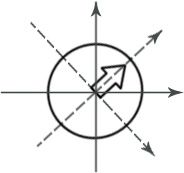
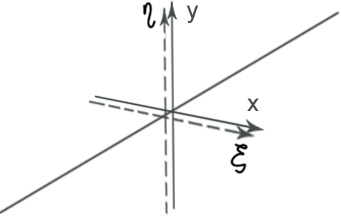
ξ,η – собственные оси.
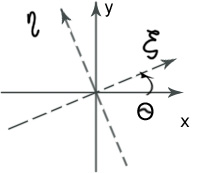
Любой поляризационно -анизотропный элемент имеет 2 собственные оси: ξ,η. Свойство собственных осей- поляризация входящей волны, параллельная собственным осям, остается такой же на выходе.
Собственные
поляризации:
![]() и
и
![]() ,
,
![]()
Матрица поляризатора, развернутого на угол Θ относительно осей х, у:
![]()
Где
![]() - пересчитывает координаты поляризационного
вектора из (х,у) в (ξ,η)
- пересчитывает координаты поляризационного
вектора из (х,у) в (ξ,η)
![]() - обратная операция:
из (ξ,η) в (х,у).
- обратная операция:
из (ξ,η) в (х,у).
![]() -
оператор в собственных осях.
-
оператор в собственных осях.
![]() ,
,
![]()
![]() ,
,
![]()
7. Фазовые платинки как поляризационно-анизотропные оптические элементы.
Фазовая пластинка имеет двулучепреломление- разные показатели преломления обыкновенной и необыкновенной волны (разные фазовые набеги).
 (nнеоб=
nη,
nоб=nξ
)
(nнеоб=
nη,
nоб=nξ
)
Фазовый
набег:
![]() ,
,
![]() ,
,
![]()
Матрица
фазовой пластинки в собственных осях
![]() =
=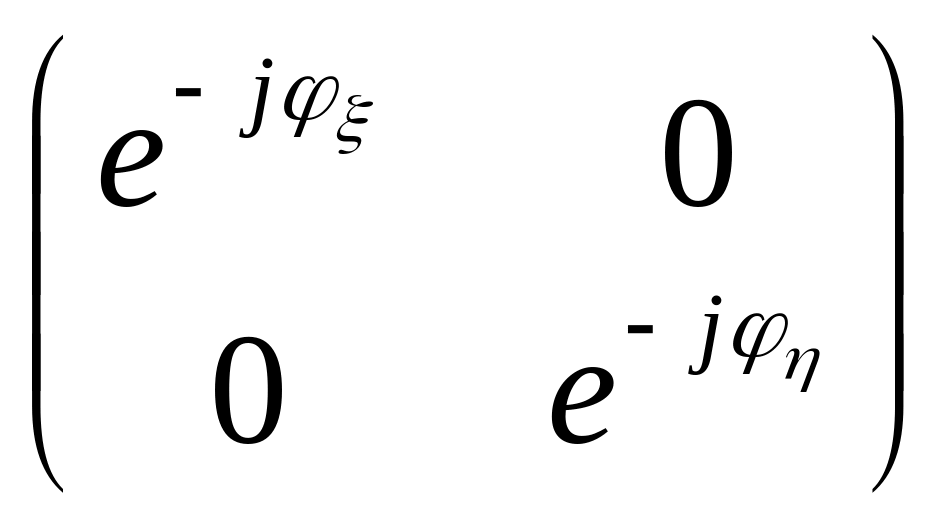 :
:
 ,
,
=![]()
Рассмотрим частные случаи.
1.
Пластинка λ/4 ,
![]() =π/2
=π/2
![]() -
матрица пластинки в собственных осях.
-
матрица пластинки в собственных осях.
2. Пластинка λ/2 , = π
![]()
При прохождении световой волны через данную пластинку на выходе получается ортогональная поляризация
Пример: правокруговая поляризация переходит в левокруговую:
![]()
Произвольный угол между ξ и х
Матрица фазовой пластинки с произвольным радиусом:
![]()
Можно показать, что:
![]()
Фазовая пластинка- это фазовый поляризационный элемент.
Поляризатор- это амплитудный поляризационный элемент.
Запишем матрицу произвольного поляризационного элемента в собственных осях (диагональная матрица):
![]()
У
идеального поляризатора
![]() =1,
=1,
![]() =0
=0
Вывод:
Любой поляризационно-анизотропный элемент имеет 2 собственные оси:
,
,
![]() ,
где Θ-угол между ξ и х.
,
где Θ-угол между ξ и х.
=![]()
![]() =
=
Комплексное
число z=|z|![]() =|z|(cos(argz)+jsin(argz))
=|z|(cos(argz)+jsin(argz))
8. Оптический вентель.
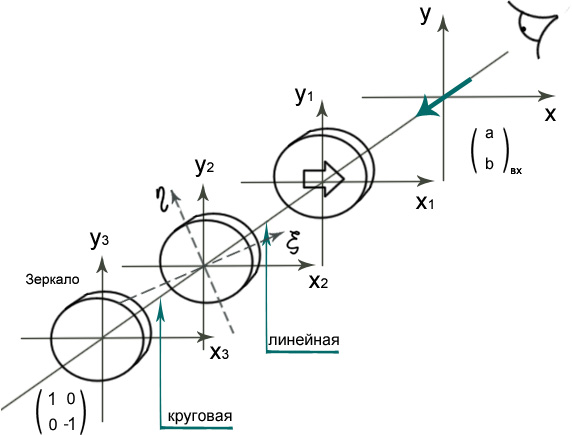
От зеркала отражается круговая поляризация, она переходит в круговую, но противоположного направления.
При расчетах необходимо учитывать правило знаков:
![]()
![]()
Применение оптического вентеля:
1. Интерферометр Майкельсона.
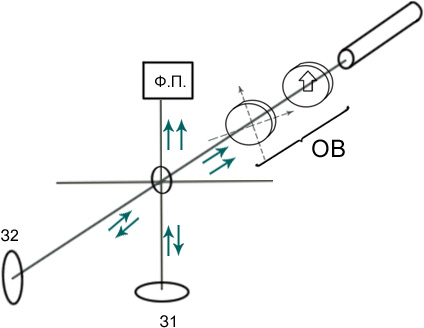
Отраженная волна нежелательна, она нарушает работу лазера. Поэтому используют оптический вентель (ОВ)
2. Многокаскадная схема.
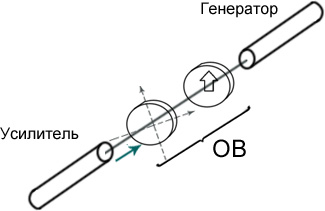
Отраженный луч (обозначен синим) нарушает работу генератора. Для его подавления используют оптический вентель.
9. Преобразование поляризации в полуволновой фазовой пластинке.
Рассмотрим преобразование поляризации в полуволновой фазовой пластинке:
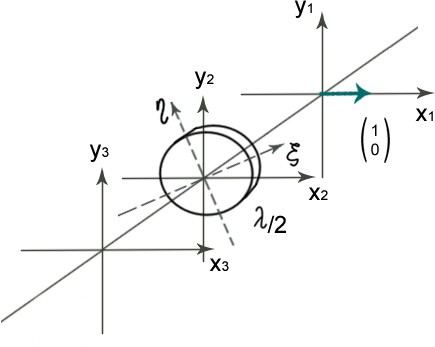
![]() =
=
=
=![]() =
=![]()
![]()
![]() =
=![]() (линейная поляризация с азимутом 2Θ)
(линейная поляризация с азимутом 2Θ)
Полуволновая пластинка часто используется в схемах для согласования поляризации опорного и сигнального пучка ( интерферометрия, голография и т.д.)
10. Фазовая пластинка вращается с постоянной скоростью.
1.
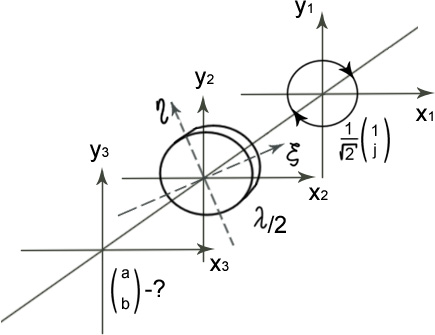
Угол между ξ и х меняется по закону: Θ=Ωt
На
входе имеется правокруговая поляризация
![]()
![]()
![]() =
=![]() =
=![]()
![]() ,
учитывая, что
,
учитывая, что
![]() и вынося -j
из выражения
и вынося -j
из выражения
![]() =
=![]() ,
получаем:
,
получаем:
![]() =
=![]() (
(![]() -левокруговая
поляризация)
-левокруговая
поляризация)
Волна описывается выражением:
![]() ,
частота выходного излучения получает
частотный сдвиг
,
частота выходного излучения получает
частотный сдвиг
![]() :
:
![]()
Применяются пластинки, вращающиеся с постоянной скоростью в двулучевом интерферометре, как устройства сдвига частоты:
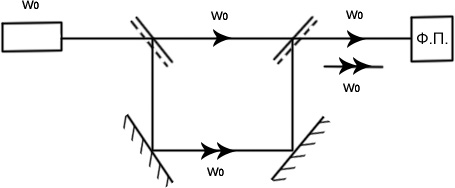
На выходе нулевые биения (сигнал постоянного тока)
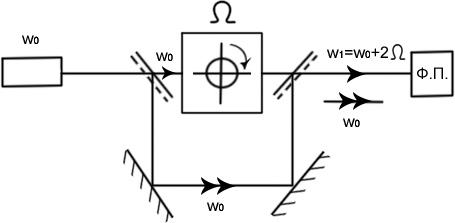
![]() -световые биения.
-световые биения.
