2. Перестройка частотного спектра резонатора.

Длина резонатора может слегка меняться (доли ). При этом происходит изменение частотного спектра.

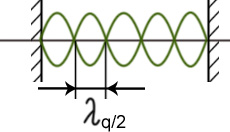
При сдвиге частоты могут совместиться. Чтобы частота сдвинулась и совместилась с соседней, необходимо, чтоб длина резонатора изменилась на /2

5. Добротность резонатора

Понятие добротности вводится в теории колебаний, оно связано с затуханием.

Например, для колебательного контура (L,C):

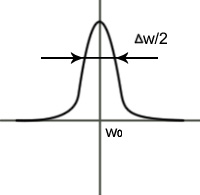
-временное представление. Добротность: (чем добротность лучше, тем уже характеристика: )

В случае лазера необходимо учитывать также тип колебаний: Q_mnq

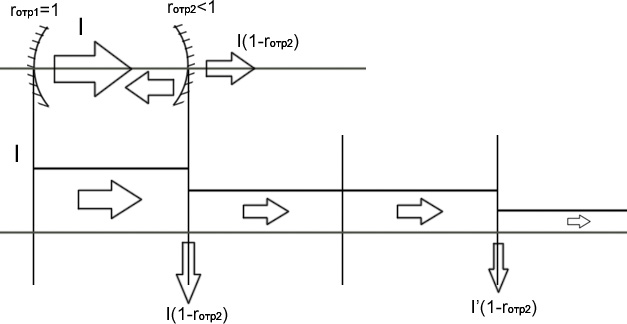
где r_отр1=1, r_отр2<1 – коэффициенты отражения зеркал.

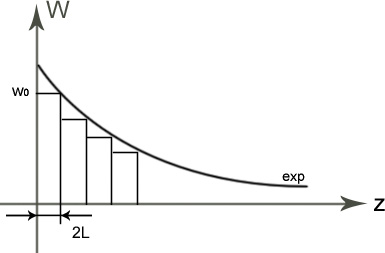
Энергия: , где ρ-объемная плотность энергии электромагнитного поля.

, , Следовательно:

Пространственный параметр потерь: Данное выражение записано для частного случая, когда , общем случае, вместо стоит Т - коэффициент передачи через 2L (за двойной проход)

Где - потери в резонаторе

Аналогичное рассмотрение можно использовать и для временного представления:

,

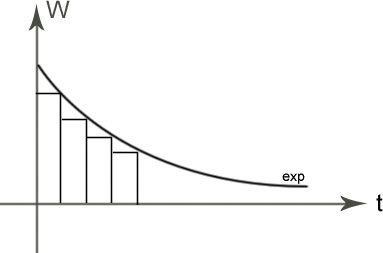
Временной параметр потерь: (время жизни фотона в резонаторе) ,

Амплитуда поля: (коэффициент 2 появляется т.к. I=A²)

Если использовать преобразование Фурье можно получить комплексный спектр и энергетический спектр :

= =…=

=

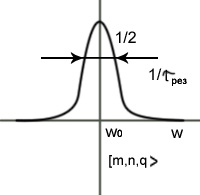
Резонансная мода:

, где -сумма всех видов потерь в резонаторе.

Потери:

1. Полезные – связаны с выводом излучения из резонатора через зеркала.

2. Вредные- поглощения в зеркалах, дифракционные потери, поглощение в активной среде, рассеяние, френелевское отражение.

6. Критерий малости дифракционных потерь.

Если a(z₁)<<a_зер1, то затекание световой волны за зеркало мало (можно пренебречь)

Если a(z₁)≈ a_зер1, световая волна начинает затекать за зеркало и необходимо учитывать дифракционные потери.

Если a(z₁)>>a_зер1, то дифракционные потери велики.

Нужно стремиться, чтоб поле моды на краях зеркала было минимально.

(аналогия- дифракция на щели) Критерий малости: Q_дифр<<Q_{геометрич}.

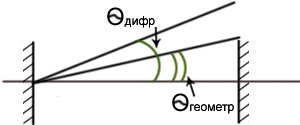
Q_дифр = λ/2а₁, Q_{геометрич}=а₂/L , λ/2а₁<<а₂/L, 2а₁а₂/ λL>>1,

а1а2/ λL>>1

а₁а₂/ λL=N_фр>>1 – число Френеля.

Nфр>>1

Распределенный параметр потерь: α_{диф.пот.} (потери от [r_отр1, r_отр2], дифракционные потери [a_зер1, a_зер2]: чем больше число Френеля, тем меньше потери:

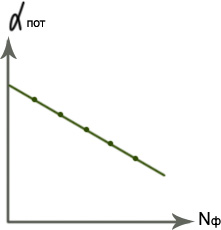
7. Элементы дифракционной теории лазерных резонаторов.

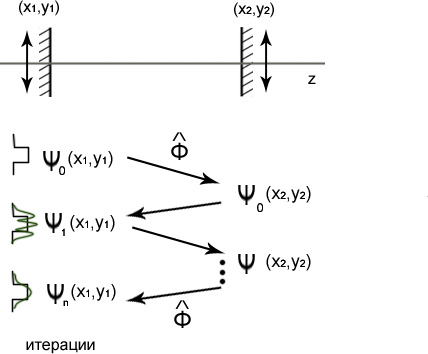
- Задача на собственные функции (моды ) и собственные значения ( ) для интегрального оператора Френеля .

Это интегральное уравнение 1-го рода, путь решения- итерационный, при котором начальное значение распределение может быть теоретически произвольным (моды формируются в процессе генерации)

Физический смысл =| |е^{-j arg}

1) | | - отвечает за изменение амплитуды, 1-| |² – определяет дифракционные потери.

2) arg отвечает за дополнительный сдвиг фаз, который приобретает волна (дополнительные фазовые набеги, обусловленные дифракцией)

Это влияет на баланс фаз, на частотный спектр.

,

Существенные параметры резонатора:

1) Частотный спектр { }

2) Потери в резонаторе { α_{.пот mnq.} , Q_mnq, τ_mnq}

Резонатор формирует каустику пуска- распределение поля в резонаторе и за его пределами.

Геометрические параметры распределения поля: {a(z₁), a(z₂), ka₀²/2, d₁, d₂, Θ_расх}

Резонатор характеризуется: {R₁, R₂, L, r_отр1, r_отр2, a₁,a₂}

,

g₁=1-R₁/L , g₂=1-R₂/L

обобщенные параметры: G₁=g₁ , G₂=g₂

обобщенные параметры координат: X₁= , X₂=

- независимые распределения.

Обобщенное дифракционное уравнение резонатора:

Частный случай:

1. Конфокальный резонатор G₁=0=G₂, N_ф>>1

-преобразование Фурье.

Такое интегральное уравнение может быть решено точно:

- гауссов пучок.

Если число Френеля конечное N_ф<1 - уравнение имеет другое решение. Полученное решение относится к конфокальному резонатору только при условии, что N_ф>>1.

При конечных значениях числа Френеля исходное уравнение:

принимает вид:

Это уравнение имеет точное решение в виде специальных функций – сфероидальных вытянутых угловых функций и вытянутых радиальных функций.

- распределение поля на зеркалах.

Собственные числа :

= (отвечает за амплитуду и дополнительную фазу)

Где , - сфероидальные вытянутые угловые функции, , - вытянутые радиальные функции (ф-я Ламера).

Графики: (номограммы)

Для иллюстрации решения резонатора рассмотрим график распределения поля на зеркале резонатора для двух числе Френеля.

(результат точного оптического расчета)

Мода TEM₀₀

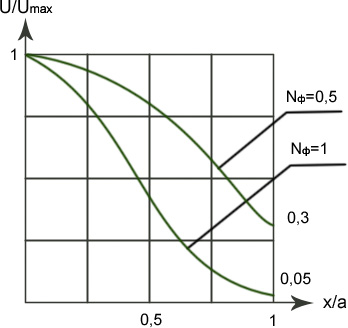
x/a=1- край зеркала.

Вывод:

Увеличение числа Френеля приводит к резкому уменьшению амплитуды поля на краю зеркала, что резко уменьшает дифракционные потери. Это распределение похоже на ТЕМ₀₀

Единственный резонатор, решаемый точно- это конфокальный.

Мода TEM₀₁

Рассмотрим распределение поля на апертуре зеркала для моды 01.

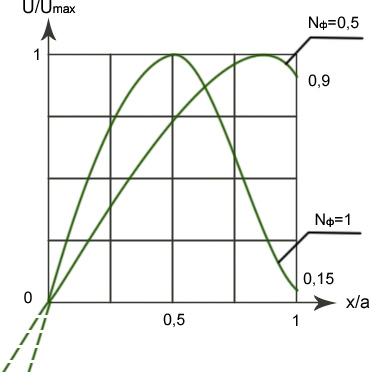
1. Если увеличивается число Френеля- поле на краю зеркала резко уменьшается

2. Сопоставляя графики приходим к выводу- у мод высшего порядка дифракционные потери больше, чем для мод 00

Номограмма для КФ резонаторов (зависимость дифракционных потерь от числа Френеля)

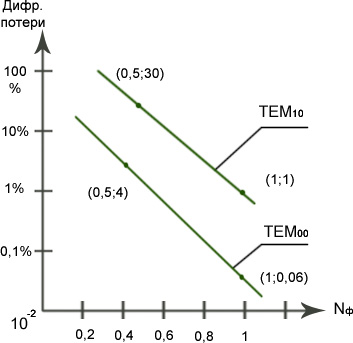
Логарифмический масштаб (поэтому прямые линии)

Графики для мод ТЕМ₀₀ и ТЕМ₁₀

Плоский резонатор:

Для плоскопараллельного резонатора отсутствует собственная каустика. Задачу можно решить только численными методами –методом итераций.

На 100-300 шаге итерации начинает устанавливаться распределение поля, которое все точнее и точнее воспроизводится.

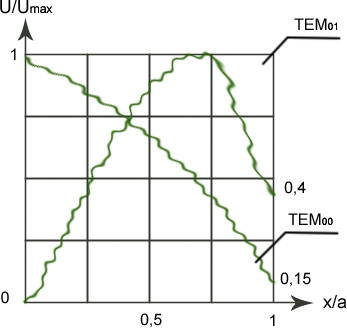
При этом симметрия исходной итерации сохраняется.

???

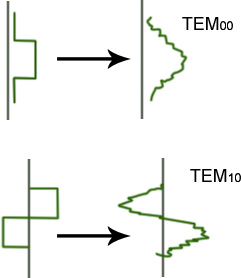Сравниваем с КФР:

Дифракционные потери в ППР гораздо больше, чем в КФР (см края зеркал)

Для сравнения дифракционных потерь КФР и ППР построим линии дифракционных потерь на номограмме