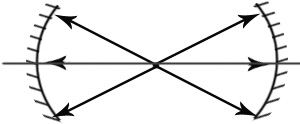
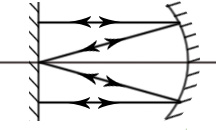
- •1. Принцип Гюйгенса.
- •2. Гауссов пучок.
- •3. Лазерные пучки высшего порядка.
- •4. Комплексный параметр Гауссова пучка.
- •5. Алгоритм расчета системы (гауссов пучок).
- •2. Введение в теорию лазерных резонаторов.
- •3. Алгебра резонатора
- •4. Частотный спектр лазерного резонатора.
- •2. Перестройка частотного спектра резонатора.
- •5. Добротность резонатора
- •6. Критерий малости дифракционных потерь.
- •7. Элементы дифракционной теории лазерных резонаторов.
- •8. Метод эквивалентного конфокального параметра.
- •3. Основы поляризационной теории лазерных пучков.
- •1. Линейная поляризация.
- •3. Эллиптическая поляризация.
- •4. Диаграмма Пуанкаре.
- •5. Основные свойства поляризационных векторов и описываемых ими состояний поляризации лазерного луча.
- •3. Физический смысл ортогональности поляризации.
- •6. Матричное описание поляризационно-анизотропных оптических элементов
- •7. Фазовые платинки как поляризационно-анизотропные оптические элементы.
- •2. Вращающаяся четвертьволновая пластинка.
- •11. Электрооптический амплитудный модулятор.
- •12. Поляризационный эффект Фарадея.
- •2) Эффект Фарадея.
- •3) Применение эффекта Фарадея.
- •4.Поляризационные методы расчета лазерных резонаторов.
- •1. Собственные поляризации резонатора.
- •2. Физический смысл модуля и аргумента
- •3. Пример.
- •2. Одночастотная генерация.
- •5. Методы селекции частот и мод в лазерных резонаторах.
- •1. Селекция переходов (выделение требуемой длины волны)
- •2. Фильтры.
- •3. Дисперсионные элементы в резонаторе как элементы селекции длин волн.
- •4. Дифракционная решетка в резонаторе для селекции длин волн.
- •1. Селекция поперечных типов колебаний в лазерных резонаторах.
- •2. Использование призм полного внутреннего отражения (пво) для селекции поперечных мод.
- •3. Методы селекции частот (продольных типов колебаний)
- •1. Поляризационно-частотные методы селекции.
- •2. Селекция частоты в лазерах с однородным контуром усиления.
- •3. Применение внутрирезонаторных многолучевых интерферометров для селекции частот.
- •3. Методы стабилизации частоты лазерного излучения.
- •1. E(t) – поле в резонаторе.
- •2. P(t) - поляризация.
- •3. Δn(t) – инверсия населенностей.
- •2. Режим нестационарной генерации.
- •3. Режим модуляции добротности.
- •4. Режим синхронизации мод.
- •1. Уравнения для электромагнитных колебаний.
- •2. Уравнения для поляризации и инверсии населенностей.
- •1. Основные положения квантовой механики.
- •2. Дипольный момент.
- •4. Эрмитовы операторы:
- •6. Значение дипольного момента:
- •7. Инверсия.
- •8. Поляризация.
- •3. Усиление световой волны в активной среде.
- •1. Проведем анализ уравнения (1)
- •2. Проведем анализ уравнения (2)
- •3. Проведем анализ уравнения (3)
- •4. Рассмотрим уравнение инверсии для стационарного случая.
- •5. Нестационарный режим генерации (динамический режим) в резонаторе.
- •6. Приведение трехуровневой системы к двухуровневой.
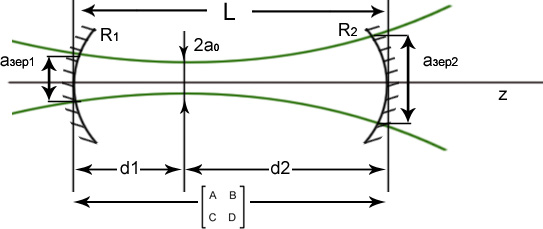
2. Введение в теорию лазерных резонаторов.
1. R1,R2- радиусы кривизны зеркал резонатора.
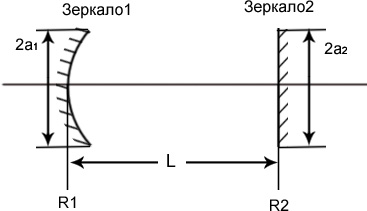
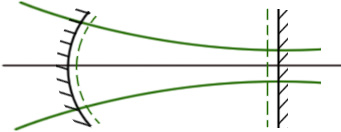
Если линейный лазерный резонатор устойчив, то существует лазерный пучок, который совмещается с резонатором.
Зеркало1: волновой фронт ГП совпадает с зеркалом
Зеркало2: волновой фронт ГП плоский (совпадает с зеркалом)
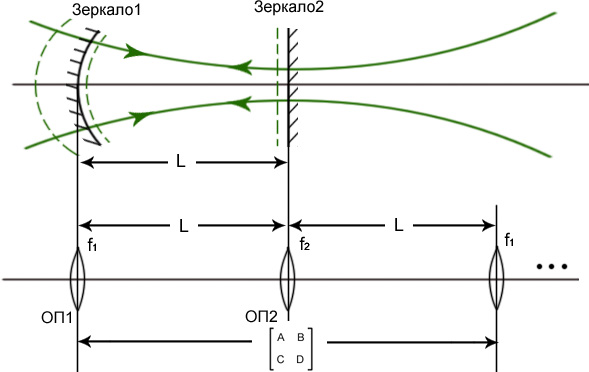
![]() ,
,
![]()
Развернув линейный резонатор в линзовый волновод мы можем воспользоваться выводами об устойчивости линзового волновода.
При каких конфигурациях R1,R2,L резонатор будет устойчивым?
Условие
устойчивости лазерного резонатора:
![]()
Матрица
двойного прохода резонатора
![]() Lрез=>f2
=> Lрез=>f1
Lрез=>f2
=> Lрез=>f1
Вычисление матрицы двойного прохода дает результат:

-2≤A+D≤2, 0≤(2+A+D)/4≤1
Проведя подстановку А и D в это выражение, получаем:
![]()
Если
перейти на язык
![]() =g1
и
=g1
и
![]() =g2,
получаем
=g2,
получаем
Критерий устойчивости лазерного резонатора:
|
|
2. Существует такой гауссов пучок, который согласован с геометрией резонатора.
|
Нельзя создать ГП, согласованный с резонатором (стоит на границе устойчивости) |
|
Можно создать ГП, согласованный с резонатором (устойчив) |
|
Нельзя создать ГП, согласованный с резонатором (неустойчив) |
Диаграмма устойчивости.
Критерий
устойчивости:
,
где
![]() -конфигурация
резонатора
-конфигурация
резонатора
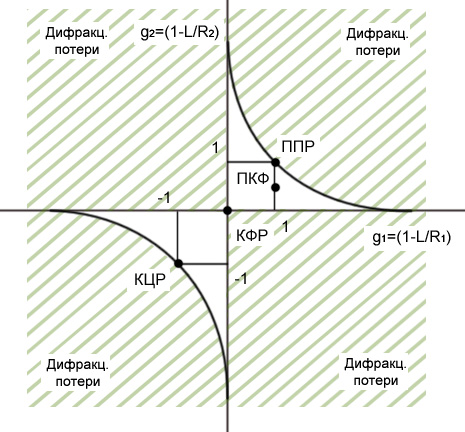
На данной диаграмме штриховано там, где не выполняется условие устойчивости.
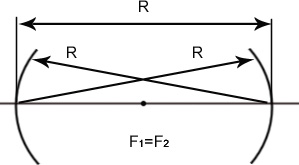
1) Конфокальный резонатор. (КФР)
Пусть
g1=g2=0,
=![]() :
L=R1=R2
в этом случае F1=F2
:
L=R1=R2
в этом случае F1=F2
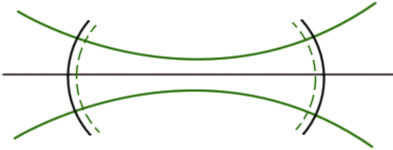
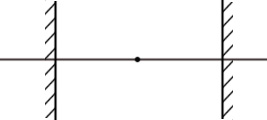
2) Плоскопараллельный резонатор. (ППР)
Пусть
=![]() , следовательно R1=
R2=
, следовательно R1=
R2=
3) Концентрический резонатор (КЦР)
Пусть
=![]() ,
L/R1=2,
L=2R1.
,
L/R1=2,
L=2R1.
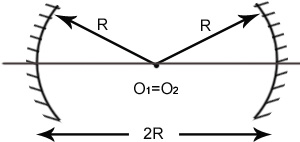
Пусть:
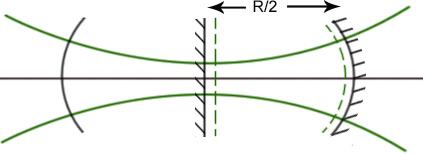
R1= , g1=1, g2=1/2
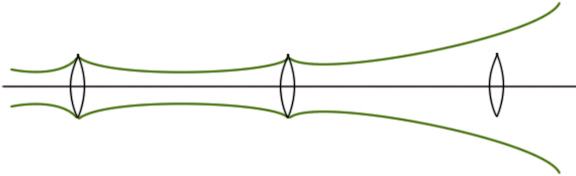
Можно выбрать разные геометрии резонатора, чтоб была одна и та же каустика.
Неустойчивые резонаторы обладают большими дифракционными потерями. (они связаны с затеканием световой волны за апертуру зеркала)
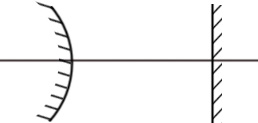
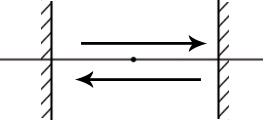
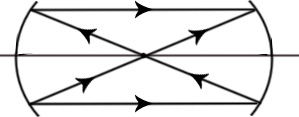
Ход лучей в резонаторах:
ППФ
|
КФР
|
КЦР
|
ПКФ
|
Геометрический лучевой смысл устойчивости резонатора:
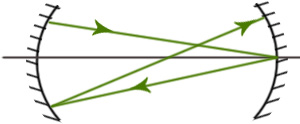 -
ход лучей
-
ход лучей
Устойчив
|
Неустойчив
|
3. Алгебра резонатора
Связывает параметры резонатора с параметрами Гауссова пучка.
Комплексный параметр гауссова пучка:
![]() ,
=
,
,
=
,
Используя
правила знаков, получаем: d1=-z1,
z1=![]()
|
|
|
|
||
4. Частотный спектр лазерного резонатора.
1. Частотный спектр лазерного резонатора вытекает из условия баланса фаз.
Для линейного резонатора:
![]()
![]()
![]()
Фаза
гауссова пучка:
![]()
Один проход кратен π. Ф(z1)-Ф(z2)=qπ, |z2-z1|=L (длина резонатора)
Ф(0,0,z)=-kmnz+(m+n+1)arctg(2z/kmna02)
kmn=2πνmn/c
-k(z1-z2)+(m+n+1)[arctg(2z1/ ka02)-arctg(2z2/ ka02)]= qπ
![]() ,
где Q=
- конфокальный параметр.
,
где Q=
- конфокальный параметр.
Воспользовавшись тригонометрическими формулами разницы arctg, преобразованием arctg=>arccos, получаем:
|
- каноническая форма частоты для моды.
Формула содержит в себе критерий устойчивости:
Пусть m=n=0 (волна типа 00)
![]()
Частотный спектр – это множество (дискретный ряд) собственных частот мод резонатора.
Мода – это тип колебания в резонаторе. Моды бывают продольные и поперечные.
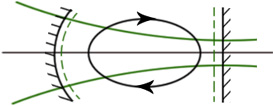
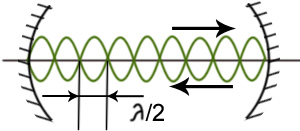
1. Продольная мода:
Условие
устойчивости -
![]() ,
,
![]() ,
,
![]() -продольный
тип колебаний.
-продольный
тип колебаний.
2. Поперечная мода: ТЕМmn
Т.о. мода-объемная структура поля в резонаторе. Она определяется индексами поперечной моды m, n и индексом продольной моды q. (это определяет волны в резонаторе.)
Мода:
![]()
![]()
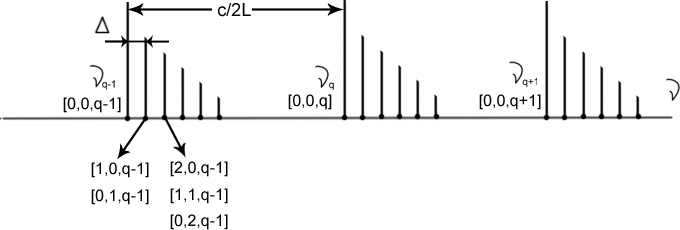
Чем выше порядок поперечных колебаний, тем ниже добротность контура (большие потери)
Чтобы частоты были вечественными, необходимо выполнение условия (см. диаграмму устойчивости)
Если
![]() ,
то
,
то
![]() ,
,
![]() -
затухания (дифракционные потери)
-
затухания (дифракционные потери)