7. Инверсия.

Для получения динамического уравнения для поляризации необходимо знать какому уравнению подчиняются и

Обоснуем уравнение движения для матрицы плотности:

( ) (из уравнения Шредингера находим с_m и с_n , далее находим )

1) Уравнение Шредингера для динамической системы.

-уравнение движения

, в уравнение подставляем как линейную суперпозицию и получаем уравнения для с₁ и с₂ в отдельности.

подставляем в уравнение:

, получаем (произведение матриц)

- коммутатор.

-Уравнение движения матрицы плотности.

8. Поляризация.

Поляризация P (сумма дипольных моментов в единице объема)

P=N_общ , где:

-оператор дипольного момента

- средняя величина квантово-механическая

- средняя величина по ансамблю

N_общ – число частиц в единице объема

=

-гамильтониан, оператор полной энергии.

, - может быть 2 состояния, и .

В общем случае , где -без взаимодействия, -дипольное взаимодействие.

,

Энергия взаимодействия : ,

Гамильтониан всей системы: =

Уравнение для каждого матричного элемента матрицы плотности:

,

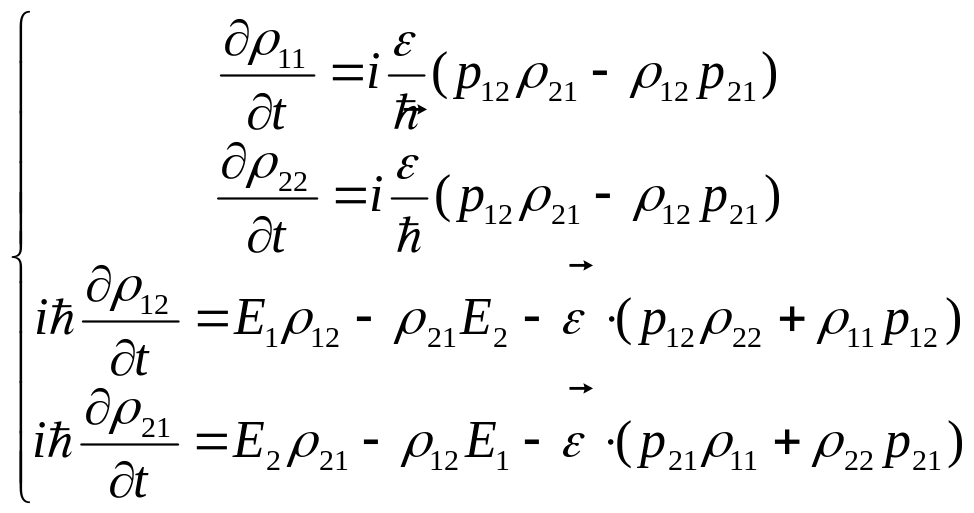
N₁=N_общ , N₂=N_общ , ,

Если посмотреть на уравнения 1 и 2, то при поле =0 населенности должны остаться теми же, как и во время генерации.

«От руки» мы должны дописать слагаемое – релаксационные члены (в отсутствии поля генерации)

где Т1 –время продольной релаксации, Т2 –время поперечной релаксации.

Уравнения учитывают релаксационные члены.

Надо получить уравнение для поляризации и инверсии населенностей.

Для инверсии населенностей.

,

Из уравнения (2) вычтем (1), из (4) –(3)

, где

Исключаем :

Возьмем производную от (***), в правой части выразим из (**), величину в (**) заменим из (***)=> исключение

II

Поляризация ведет себя как осциллятор.

Посмотрим на (*), нужно исключить используя (***) для получения уравнения для инверсии населенностей.

III

I

Где:

- инверсия, приведенная к одной частице

P_m –«проекция» поляризации на m-ю моду (часть поляризации, «раскачивающая» данную моду)

Данные уравнения описывают колебания в резонаторе.

Если рассматривать усиление сигнала вне резонатора, то уравнение I должно быть заменено уравнением бегущей волны.

3. Усиление световой волны в активной среде.

В качестве уравнения I рассмотрим уравнение бегущей волны:

,

,

= =

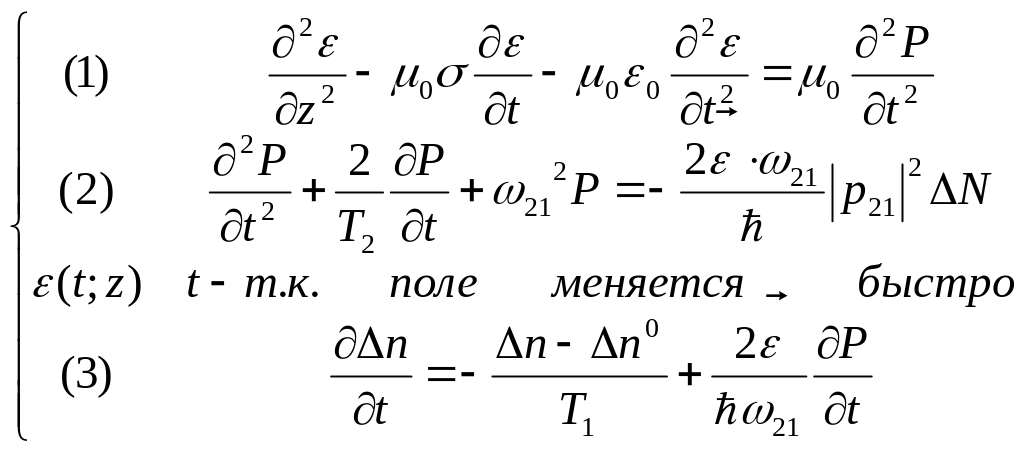
= = (к.с.-комплексно сопряженное)

Поляризация в общем случае:

Удобнее перейти на язык комплексных амплитуд.

1. Проведем анализ уравнения (1)

1) Первое слагаемое

, - поле -> =>

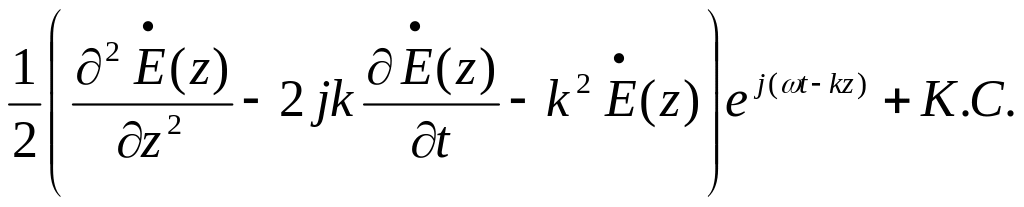
Амплитуда волны- это модуль комплексной амплитуды => пунктир- закон изменения

Скорость изменения - , и

=> Упрощение:

, поэтому можно пренебречь, таким образом при переходе к комплексным апмлитудам:

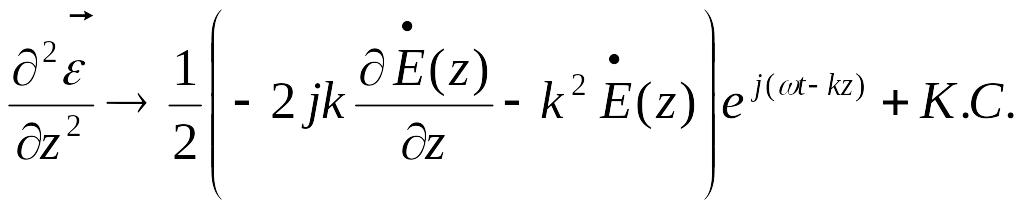
2) Второе слагаемое: -

От времени зависит только экспонента, поэтому:

3) Третье слагаемое:

Общее уравнение:

(1*)