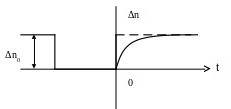
3. Δn(t) – инверсия населенностей.

Δn₀ – инверсия населенности в системе, где нет насыщения

T₁- время продольной релаксации (время изменения инверсии населенности)

Режим стационарной генерации и основные динамические режимы генерации лазеров.

1. Режим стационарной генерации.

Коэффициент усиления активной среды:

Интенсивность излучения: , Для однородного контура усиления:

- коэффициент потерь

L- размер активной среды

-параметр насыщения

G₀ – ненасыщенный параметр населения (параметр усиления слабого сигнала) – зависит от инверсии населенностей.

G(I)- для однородного контура усиления.

, , где - ненасыщенная инверсия населенностей (генерация либо отсутствует, либо мала)

В₂₁ – вероятностный коэффициент Эйнштейна, - частота перехода, δ₂₁= - сечение индуцированного перехода, ΔN=N₂-N₁

G0= δ21ΔN0

При переключении в стационарном режиме происходят переходные процессы.

I_пр – поток идет направо, I_лев – поток идет налево.

На втором зеркале: I_лев(L)- левая волна отразилась от зеркала 2 в точке L.

I_лев(L)= I_пр (L)R_отр2

На первом зеркале: I_пр (0)= I_лев (0)R_отр1

В разных сечениях z разные интенсивности, разные G(z). Но мы говорим о среднем значении -

Формула для интенсивности генерации: - выходная интенсивность генерации в стационарном режиме.

- коэффициент превышения усиления над потерями.

2. Режим нестационарной генерации.

Пусть до времени t₀ был стационарный режим генерации. Возникает переходной процесс (ΔN, R_отр2 –изменились скачком)

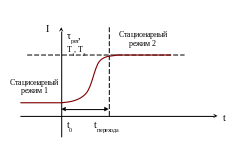
На переходной процесс влияют 3 временных параметра:

τ_рез- время жизни фотона в резонаторе

Т₁ – время продольной релаксации

Т₂ – время поперечной релаксации

При времени изменения инверсии (добротности резонатора), которое отвечает условию τ_пер>> τ_рез; Т₁; Т₂ систему можно описать уравнениями, которые приведены выше.

Но если накачка в системе не удовлетворяет уравнениям –то режим нестационарный: τ_пер<< τ_рез; Т₁; Т₂

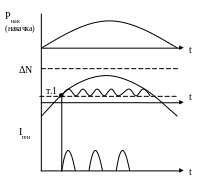
Пример нестационарного режима генерации.

Твердотельный лазер с оптической накачкой.

1) Т.к. действует накачка- изменяется инверсия (квазистационарна)

2) Не достигается ΔN_пор – нет поля в резонаторе, работает только накачка

3) Достигается ΔN_пор – в точке 1 –особенность. Когда инверсия достигает порога начинается режим генерации, растет интенсивность I, но по мере увеличения интенсивности включается процесс насыщения, инверсия уменьшается. При уменьшении ΔN интенсивность падает и при достижении порога- равняется 0.

Импульс заканчивается когда насыщенная инверсия сравняется с порогом. Но инверсия опять растет, поэтому процесс повторяется и образуется 2 импульс.

В итоге получаются регулярные импульсы, τ_имп соизмеримо с τ_рез; Т₁; Т₂

Интенсивность неоднородна в среде. Также присутствует нерегулярность:

Отдельные пики с характерным периодом между ними.

3. Режим модуляции добротности.

Время , Если - получается «пичковый» режим генерации.