- •1. Принцип Гюйгенса.
- •2. Гауссов пучок.
- •3. Лазерные пучки высшего порядка.
- •4. Комплексный параметр Гауссова пучка.
- •5. Алгоритм расчета системы (гауссов пучок).
- •2. Введение в теорию лазерных резонаторов.
- •3. Алгебра резонатора
- •4. Частотный спектр лазерного резонатора.
- •2. Перестройка частотного спектра резонатора.
- •5. Добротность резонатора
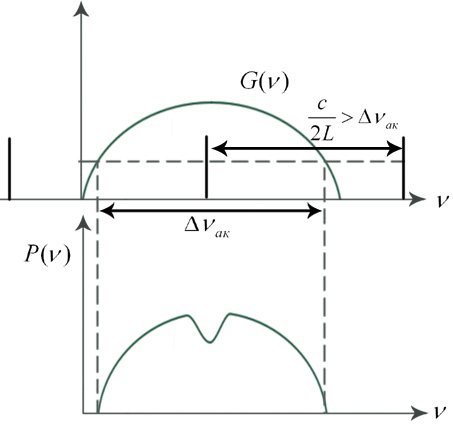
- •6. Критерий малости дифракционных потерь.
- •7. Элементы дифракционной теории лазерных резонаторов.
- •8. Метод эквивалентного конфокального параметра.
- •3. Основы поляризационной теории лазерных пучков.
- •1. Линейная поляризация.
- •3. Эллиптическая поляризация.
- •4. Диаграмма Пуанкаре.
- •5. Основные свойства поляризационных векторов и описываемых ими состояний поляризации лазерного луча.
- •3. Физический смысл ортогональности поляризации.
- •6. Матричное описание поляризационно-анизотропных оптических элементов
- •7. Фазовые платинки как поляризационно-анизотропные оптические элементы.
- •2. Вращающаяся четвертьволновая пластинка.
- •11. Электрооптический амплитудный модулятор.
- •12. Поляризационный эффект Фарадея.
- •2) Эффект Фарадея.
- •3) Применение эффекта Фарадея.
- •4.Поляризационные методы расчета лазерных резонаторов.
- •1. Собственные поляризации резонатора.
- •2. Физический смысл модуля и аргумента
- •3. Пример.
- •2. Одночастотная генерация.
- •5. Методы селекции частот и мод в лазерных резонаторах.
- •1. Селекция переходов (выделение требуемой длины волны)
- •2. Фильтры.
- •3. Дисперсионные элементы в резонаторе как элементы селекции длин волн.
- •4. Дифракционная решетка в резонаторе для селекции длин волн.
- •1. Селекция поперечных типов колебаний в лазерных резонаторах.
- •2. Использование призм полного внутреннего отражения (пво) для селекции поперечных мод.
- •3. Методы селекции частот (продольных типов колебаний)
- •1. Поляризационно-частотные методы селекции.
- •2. Селекция частоты в лазерах с однородным контуром усиления.
- •3. Применение внутрирезонаторных многолучевых интерферометров для селекции частот.
- •3. Методы стабилизации частоты лазерного излучения.
- •1. E(t) – поле в резонаторе.
- •2. P(t) - поляризация.
- •3. Δn(t) – инверсия населенностей.
- •2. Режим нестационарной генерации.
- •3. Режим модуляции добротности.
- •4. Режим синхронизации мод.
- •1. Уравнения для электромагнитных колебаний.
- •2. Уравнения для поляризации и инверсии населенностей.
- •1. Основные положения квантовой механики.
- •2. Дипольный момент.
- •4. Эрмитовы операторы:
- •6. Значение дипольного момента:
- •7. Инверсия.
- •8. Поляризация.
- •3. Усиление световой волны в активной среде.
- •1. Проведем анализ уравнения (1)
- •2. Проведем анализ уравнения (2)
- •3. Проведем анализ уравнения (3)
- •4. Рассмотрим уравнение инверсии для стационарного случая.
- •5. Нестационарный режим генерации (динамический режим) в резонаторе.
- •6. Приведение трехуровневой системы к двухуровневой.
3. Методы стабилизации частоты лазерного излучения.
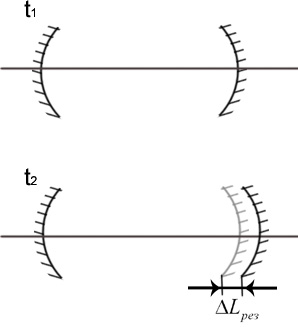
Изменение
оптического пути резонатора (от
температуры, вибрации и т.д) приводят к
изменению частоты:
![]() ,
,
![]()
Чтобы исключить факторы изменения длины резонатора, используются следующие методы:
1. Пассивные методы стабилизации:
-) абсолютно жесткий резонатор
-) использование материалов с низким коэффициентом температурного расширения (сетал - стекла, КТР 10-9)
2. Активные методы
3. Комплексные методы (активные и пассивные)
Активный метод заключается в том, что контролируется насколько процесс успел отойти от нормы и восстанавливается по обратному закону.
Активные метода предполагают активное воздействие на оптическую длину резонатора по результатам контроля.
|
|
![]()
Контролируется
![]() ,
при отклонении производится активное
воздействие- подстройка резонатора.
,
при отклонении производится активное
воздействие- подстройка резонатора.
Перемещается резонатор с помощью магнитострикции, с помощью пьезоэлектрического эффекта
Пьезоэффект
|
Магнитострикция
|
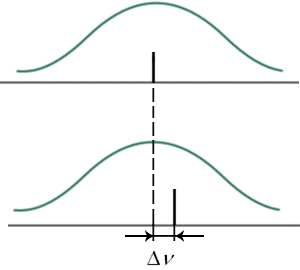
Для сравнения существует эталон. Для контроля ухода частоты необходимо иметь частотные реперы. (частотный эталон- провал Лэмба)
Провал Лэмба:
Наблюдается в зависимости мощности генерации одночастотного лазера от частоты.
(только для неоднородно уширенных контуров- газовые лазеры.)
Связан данный провал с тем, что в процессе перестройки частоты мода работает с разными группами атомов.
Лэмбовский провал строго привязан к центральной частоте лазерного перехода, на которую не воздействует ни температура, ни другие воздействия. (частотный репер)
\\----------------------------------------------------------------------------------------------------------------------
Динамика генерации лазеров.
|
P(t) – поляризация активной среды E(t) - поле (моды, сумма мод) ΔN(t)- инверсия населенностей |
Лазер – это сложная колебательно-волновая структура. В лазерной системе можно выделить 3 взаимосвязанных динамических переменных:
1. Поле
2. Поляризация активной среды
3. Инверсия населенностей.
Они описываются динамическими уравнениями (дифференциальные уравнения по времени)
![]() =…,
=…,
![]() =…,
=…,
![]() =…
=…
Колебательная система:
![]() - свободные
колебания, где
- свободные
колебания, где
![]() - время релаксации (характеризует
потери),
- время релаксации (характеризует
потери),
![]() -
собственная частота осциллятора.
-
собственная частота осциллятора.
![]() -вынужденные
колебания, где
-вынужденные
колебания, где
![]() -вынуждающая
сила.
-вынуждающая
сила.
Три фундаментальных уравнения.
Феноменологически напишем динамических уравнения:
1. E(t) – поле в резонаторе.
E(t)=
![]() - сумма отдельных мод. Моды обладают
свойством ортогональности. Рассматриваем
амплитуду отдельной моды -
- сумма отдельных мод. Моды обладают
свойством ортогональности. Рассматриваем
амплитуду отдельной моды -![]() :
:
Мода
похожа на осциллятор
![]()
Где
![]() -
частота моды (зависит от геометрии
резонатора)
-
частота моды (зависит от геометрии
резонатора)
![]() -
время жизни фотона в резонатор
-
время жизни фотона в резонатор
![]() - часто поляризации,
обусловленная модой m.
- часто поляризации,
обусловленная модой m.
2. P(t) - поляризация.
Динамическое уравнение- уравнение типа осциллятора:
![]()
T2 – время поперечной релаксации
![]() - собственная
частота осциллятора (частота лазерного
перехода)
- собственная
частота осциллятора (частота лазерного
перехода)
![]() -
нормированная инверсия населенностей
-
нормированная инверсия населенностей
р21 – матричный элемент дипольного момента
Если р21=0, то говорят, что переход запрещен- нет вынуждающей силы («раскачки» поляризации)