2. Селекция частоты в лазерах с однородным контуром усиления.

^{1. Твердотельный лазер АИГ на Nd}+

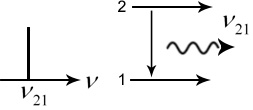
В идеальном случае есть пара уровней, на которых работает лазер:

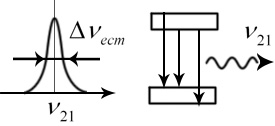
Но реально уровни расширены, поэтому существует разброс

Данные схемы представлены для одного атома. А если атомов много (ансамблю атомов), то больше излучение по амплитуде (интенсивность) Но иногда линии уширяются (например, эффект Зеемана и т.д.) Соседние атомы взаимодействуют между собой.

Реальный контур усиления: Контур усилен однородно по атомам (в одинаковых условиях)

2. Газоразрядный лазер (He-Ne)

- контур усиления с доплеровским механизмом (неоднородный)

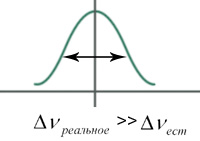
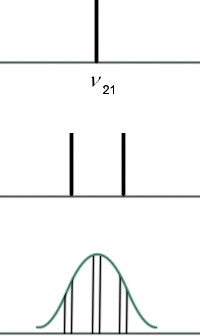
Но т.к. атомы подвижны- существует эффект Доплера. Появляется частотный сдвиг, в итоге контур уширяется. В контуре усиления выделяются интервалы, за которые отвечают группы атомов.

Т.о. однородный контур усиления если атомы не движутся, неоднородный – если атомы движутся.

Основное различие однородного и неоднородного контуров усиления:

Однородный За частоту в точке отвечают все атомы

Неоднородный За частоту в точке отвечает группа атомов

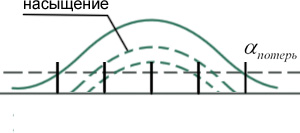
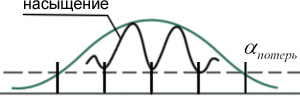
У неоднородного контура генерации появляются провалы на частоте генерации (обеспечение насыщения) Но все частоты остаются. В случае однородного контура- происходит конкуренция частот и в конце концов «выживает» та частота, которая находится ближе к максимуму усиления.

Однородный

Неоднородный

Лазер с однородно уширенным контуром усиления будет работать в одночастотном режиме при условии отсутствия эффектов пространственной неоднородности по всем продольным модам.

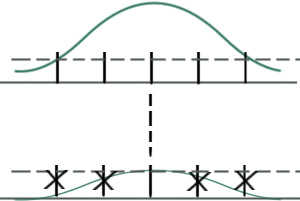
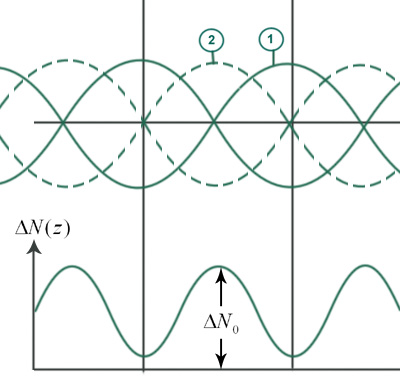
Стоячая волна в лазерном резонаторе:

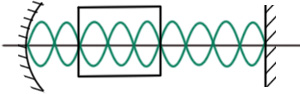
Из-за эффектов пространственной неоднородности инверсии населенностей ΔN(z) в генерацию выйдет мода 2 в тех точках, где у 1 были узлы.

Нужна пространственная однородность. Этого можно добиться следующим образом:

1. Перемещать стоячую волну - быстрое перемещение пучностей мод для получения эффекта пространственной однородности.

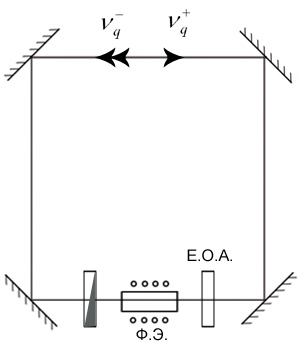
2. Переход к резонатору бегущей волны (кольцевой резонатор.)

Правая и левая волна проходят не влияя друг на друга. Частоты и одинаковы, произойдет интерференция и образуется стоячая волна. Необходимо подавить одну из волн и оставить одну бегущую волну. Для этого используется элемент фарадея и элемент с естественной оптической активностью.

3. Применение внутрирезонаторных многолучевых интерферометров для селекции частот.

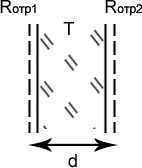
Интерферометр Фабри-Перо.

Rотр1, Rотр2 - коэффициенты отражения 1 и 2 поверхностей, Т- коэффициент пропускания. а0 – амплитуда падающей волны. Между пластинами n>1 ρ, τ –коэффициенты отражения и пропускания по амплитуде. ρ2+τ2=1

, где -фазовый набег: =k[ab], Ф=k[bcd].

Пусть =0, тогда:

-геометрическая прогрессия.

- набег фаз между а₁ и а₂, а₂ и а₃ и т.д., где -угол преломления.

От частоты зависит набег фаз:

Следовательно и - зависит от частоты

-коэффициент пропускания по амплитуде.

- коэффициент пропускания по интенсивности.

Т.к. для комплексных чисел :

Аналог формулы Эйри:

Формула Эйри: , где -фактор резкости интерферометра Фабри-Перо.

Физический смысл F – количество эффективных суммируемых пучков на выходе: , где R –коэффициент отражения по интенсивности , ρ – коэффициент отражения по амплитуде.

Графики для нескольких случаев : зависимость коэффициента пропускания T от набега фаз

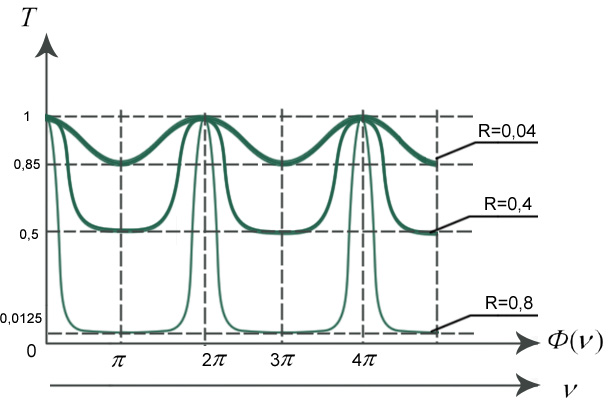
1) R=0,04 – непокрытая поверхность стекла интерферометра Фабри-Перо (стекло-воздух) Это гармоническая функция.

2) R=0,4- напыление на стекле. Гармоническая функция исказилась, возрастают селективные свойства пластины.

При увеличении R (коэф. отражения по интенсивности) F (фактор резкости) становится более контрастным.

Зависимость коэффициента пропускания T от частоты ν

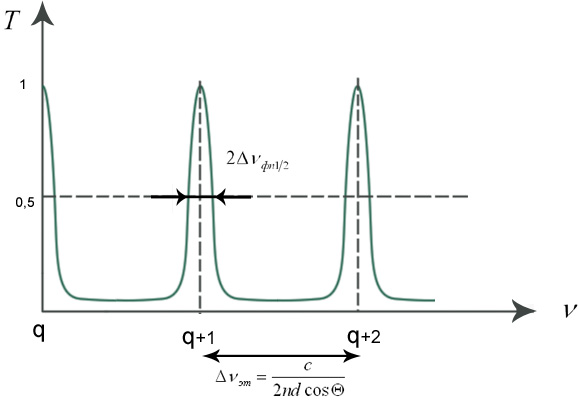
Ширина пика: - на уровне ½

,

Чем больше коэффициент отражения R –тем уже полоса фильтра.

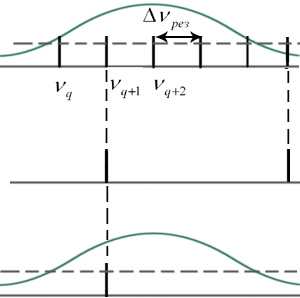
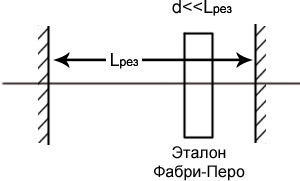
Чтобы получить одночастотный режим, можно использовать эталон Фабри-Перо. При условии, что d<<L_рез , т.о. подавляются все частоты, кроме

Эталон Фабри-Перо так же применяют для спектрального анализа излучения.

(Можно изменять ширину резонанса, меняя расстояние d или угол Θ. На этом принципе основаны перестраиваемые фильтры. )