4. Дифракционная решетка в резонаторе для селекции длин волн.

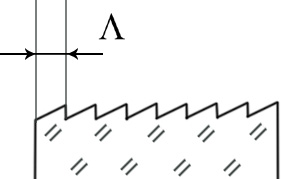
В лазерных резонаторах используются фазовые решетки отражательно типа (показатель преломления n(x) , где –период решетки )

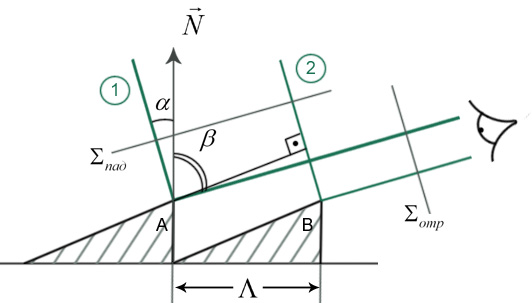
Обозначения: N-нормаль , α - угол падения, β-угол отражения.

Сравнение оптических длин пути лучей 1 и 2 показывает, что между ними возникает разность длин оптических путей , используя чертеж можно записать следующее выражение:

Условие наблюдения дифракционного максимума в направлении угла дифракции β:

- основное уравнение дифракционной решетки.

Рис.

Эффективная разъюстировка: D_реш , где -угол разъюстировки,

Т.е. для одних длин волн присутствует разъюстировка, а для других - нет.

Если продифференцировать основное уравнение решетки, получается:

D_реш = =

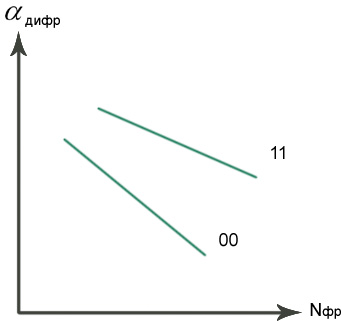
Рассмотрим частные случаи.

1. Если m=0, то D=0 , поэтому в резонаторах используют более высокие порядки дифракции (1-2)

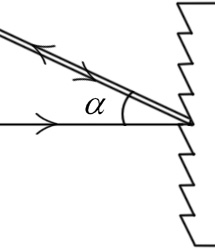
2. Автоколлимационный режим работы решетки : β=-α

1. Селекция поперечных типов колебаний в лазерных резонаторах.

1. Если есть многомодовый режим генерации.

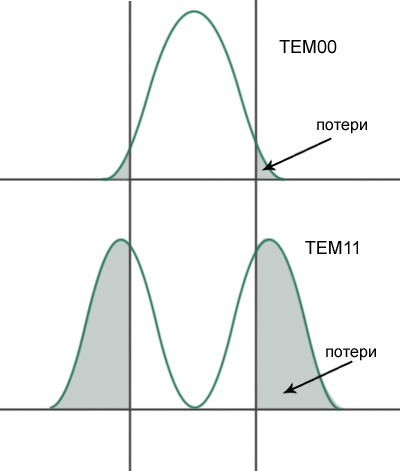
Селекция поперечных типов колебаний производится путем введения селективных дифракционных потерь.

Дифракционные потери зависят от числа Френеля (длина играет роль длина резонатора, апертура зеркал)

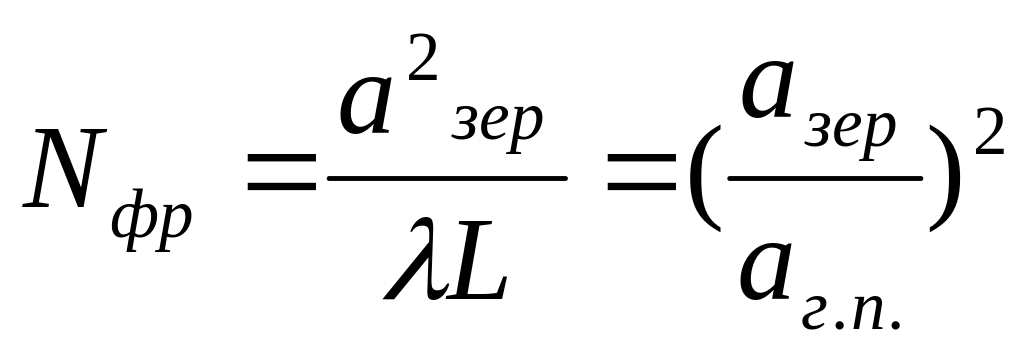
Число Френеля можно менять следующими способами:

1) Ирисовая диафрагма

2) Длина резонатора.

Если нам нужно оставить моду ТЕМ00, то необходимо так подобрать параметры, чтобы потери для ТЕМ00 были допустимые, а для других мод – критические.

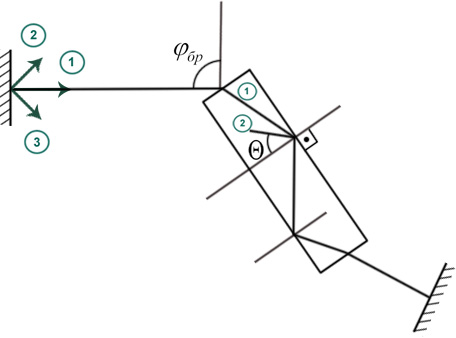
2. Использование призм полного внутреннего отражения (пво) для селекции поперечных мод.

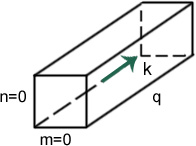
Проекции вектора к:

Высшие типы колебаний – волны с волновым вектором не вдоль оси, а под некоторым углом (широкий угловой спектр)

Где 1- это осевая мода ТЕМ00 Если распространяется другая мода (2), то для нее Θ<Θпво, больше потери. Призма вносит потери в неосевые типы колебаний – моды высшего порядка.

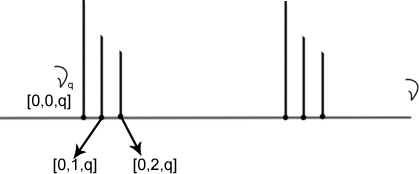
3. Методы селекции частот (продольных типов колебаний)

1. Поляризационно-частотные методы селекции.

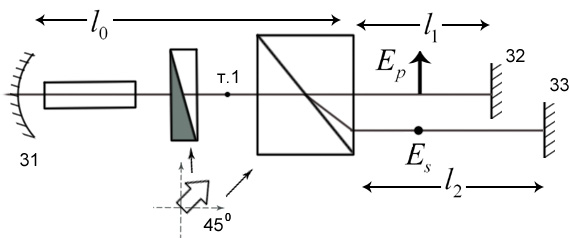
Используются 2 резонатора- один на P-поляризации, другой на S-поляризации, а так же поляризатор и поляризационную призму (расщепление луча на обыкновенный и необыкновенный)

При прохождение пучков через призму и возвращению обратно в точку 1 изменится поляризация. Появится набег фаз между P и S:

, если - то пучок не будет проходит и не будет генерации (см. диаграмму Пуанкаре)

Управляя величиной , мы можем менять добротность резонатора:

Добротность зависит от частоты, если не менять и : . Следовательно, можно производить селекцию частоты, т.к. одни частоты будут иметь большие потери, а другие меньшие.

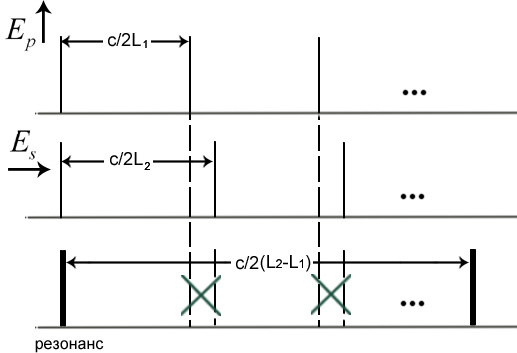
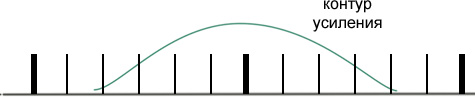
Не уменьшая длину резонатора мы отделили одну частоту. Данный метод наиболее часто используется.