1. Теория лазерных пучков.

Основы дифракционной теории лазерных пучков.

1. Принцип Гюйгенса.

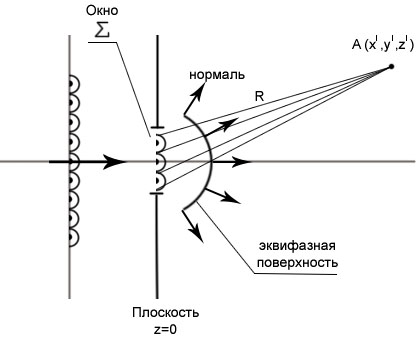
Рассмотрим падение световой волны на плоскость z=0 с окном Σ.

Каждая точка волнового фронта является источником сферической волны. Дальнейшее распространение волны определяется суммой сферических волн, проходящих в отверстие. При этом энергия передается не только в прямом направлении, но и в области геометрической тени.

Количественно: Нужно просуммировать волны, попавшие в окно Σ.

Поле в окне задано :

Где -амплитуда волны, -фаза волны в каждой точке.

Рассчитаем поле в произвольной точке А пользуясь принципом Гюйгенса.

***

Плоская волна описывается уравнением , знак – соответсвует волне, распространяющейся в направлении увеличения z, + - в противоположном направлении.

Экспоненциальная форма записи уравнения плоской волны:

Такая форма записи удобна для дифференцирования в волновых уравнениях, но физический смысл имеет только мнимая часть этого выражения.

В теории дифракции, где учитывается монохроматичность волны ( ), для удобства вычислений экспоненту не пишут (но учитывают). Уравнение плоской волны записывают в виде:

Сферическая волна Фаза волны меняется в пространстве, зависит от радиус-вектора r. Набег фазы определяется kr. Плотность потока энергии убывает обратно-пропорционально r², а амплитуда убывает обратно-пропорционально r:

***

В точку А волна попадет, пройдя расстояние R, при этом надо учесть набег фаз.

В соответствии с принципом Гюйгенса поле в т.А равно:

где интегрирование идет по всему окну, - вклад от одного элементарного источника, (x,y)-координаты точки в окне.

Расстояние: R= , подставляем в предыдущее уравнение:

2. Рассмотрим задачу в параксиальном приближении.

Углы, под которыми видна т.А –малы. При этом , <<1. Рассмотрим корень в параксиальном приближении.

= = т.к. и z=0.

Выражение для принимает вид:

3. Выражение в знаменателе можно заменить 1, т.к. в амплитуду выражение дает малые поправки, которыми можно пренебречь. В числителе в экспоненте мы не можем провести эту замену т.к. выражение оказывает существенное влияние на фазу. (Фаза определяется как , где и могут быть больше π)

учитывая нормировочный множитель и множитель, постоянный по х и у:

(переобозначение- =СФ)

Выражение описывает поле в произвольной точке А за экраном, оно определяет фундаментальное для физической оптики интегральное преобразование - преобразование Френеля .

Рассмотрим уточнение преобразования Френеля.

4. Вынесем за знак интеграла множители, не содержащие переменных интегрирования:

=

Переобозначим =Сf

Приближение Релея: если , то можно пренебречь фазой.

, , , где а –размер окна. Если точка очень далека от экрана, то с некоторого расстояния z’ условие начнет выполняться.

L- расстояние от окна до т. наблюдения, . Комбинация чисел носит название число Френеля: N_фр=

Рассматриваются такие области, где N_фр<<1, область пространства, где выполняется данное соотношение называется дальней зоной (зоной Фраунгофера)

, , (пространственная частота)

преобразование Фурье

***

Преобразование Фурье.

Если есть функция f(t) (закон, сигнал), то функцию - называют преобразованием Фурье. (комплексный спектр функции)

Обратное преобразование Фурье:

Преобразование Фурье- переход от сигнала к спектру.

***

В дальней зоне работает преобразование Фурье (мы перешли от преобразования Френеля к преобразованию Фурье)

Области:

I – Область геометрической тени - L≈λ (не успевают сработать дифракционные эффекты, т.к. поле не затекает в область геометрической тени)

II – Ближняя зона – работает преобразование Френеля

III – Дальняя зона – работают преобразования Френеля и Фурье .