Тема 5 Применение индексного метода в анализе социально-экономических явлений

Тема лабораторного занятия

Индексный анализ изучаемого явления по совокупности разнородных элементов

Задача 1

Задание. На основе данных о количестве проданного товара торговой фирмой и ценах за единицу товара (за 1 кг) проанализировать изменение стоимости проданных товаров за счёт отдельных факторов в относительной форме (с помощью индексов) и абсолютной форме. Для анализа использовать индексную модель, учитывая то, что совокупность товаров разнородна по своей натурально-вещественной форме и назначению.

Решение

На основе данных о модальной цене товара и количестве проданного товара определим фактическую стоимость проданных товаров ( товарооборот) в базисном (в мае) и отчётном периоде (в октябре),\. Введём также показатель условной стоимости проданных товаров в отчётном периоде, исчисленной в базисных ценах

Исходные данные и расчётные показатели представлены в таблице 1

Таблица 1 – Цены, количество и стоимость проданных товаров за два периода.

Товар	Количество, т		Цена за 1 кг, руб.		Стоимость проданных товаров.тыс. руб.
	май q0	октябрь q1	май p0	октябрь p1	май p0q0	октябрь p1q1	условная p0q1
А	62	64	26,50	33,30	1643,00	2131,20	1696,00
Б	58	68	64,34	87,17	3731,72	5927,56	4375,12
В	72	70	33,28	44,03	2396,16	3082,10	2329,60
Итого	х	х			7770,88	11140,86	8400,72

Индивидуальные индексы рассчитываются по формулам:

цен

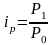
объема реализации

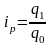
стоимости продаж (товарооборота) ,

где 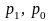- цена единицы товара в отчетном и базисном периодах (в октябре и мае), соответственно

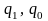- объем (количество) проданного товара в отчетном и базисном периодах

- стоимость проданного товара в отчетном и базисном периодах

Результаты расчетов индивидуальных индексов приведены в таблице 2

Таблица 2 - Индивидуальные индексы цен и физического объема проданных товаров.

	Индивидуальные индексы
	ip	iq	ipq
А	1,257	1,032	1,297
Б	1,355	1,172	1,588
В	1,323	0,972	1,286

Данные показывают, что в октябре по сравнению с маем произошел рост цен на :

товар « А» - на 25,7 %

товар «Б» - на 35,5 %

товар В - на 32,3 %

Увеличился объем продаж товара «А» - на 3,2 % и товара «Б» - на 17,2%. Снизился объем продаж товара «В» - на 2,8 % (97,2 % - 100 %). В результате изменения цен и объема продаж стоимость проданных товаров увеличилась следующим образом:

товара « А» - на 29,7 %

товара «Б - на 58,8 %

товара «В» - на 28,6 %

Основным фактором увеличения стоимости продаж (товарооборота) явилось повышение цен.

Общие индексы.

Индекс цен

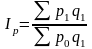
где - общая стоимость проданных товаров в отчетном периоде (в октябре) в ценах базисного периода (май)

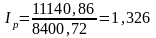
Индекс характеризует общее повышение цен в октябре на 32,6%

Индекс физического объема товарооборота

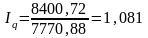
Объем реализации товаров увеличился в октябре по сравнению с маем на 8,1%.

Индекс стоимости проданных товаров (товарооборота)

Рассчитанные индексы взаимосвязаны и составляют следующую модель:

Товарооборот по совокупности товаров (продуктов) увеличился в октябре по сравнению с маем на 43,3% в результате повышения цен на 32,6% и увеличения физического объёма товарооборота на 8,1%.

Определим абсолютный прирост товарооборота ( ) и разложим по факторам.

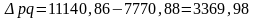(тыс. руб.)

Общий прирост товарооборота составил 3369,98 тысяч рублей

в том числе за счёт увеличения:

а) физического объёма товарооборота

б) цен

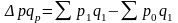
Таким образом, 81,3% общего прироста товарооборота (2740,14: 3369,98*100) связано с повышением цен, и 18,7% (629,84: 3369,98 *100) - с увеличением физического объёма товарооборота.

В задаче были использованы формулы агрегатных индексов цен и физического объёма проданных товаров.

Построим указанные индексы как индексы средние из индивидуальных.

Средний гармонический индекс цен:

Средний арифметический индекс физического объёма проданных товаров:

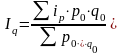
Результаты расчёта индексов, построенных в разной форме, совпадают. Результаты расчёта индексов могут иметь незначительные расхождения, связанные с округлениями при расчётах.

.

Варианты индивидуальных заданий

Таблица 3 – Цены и количество проданных товаров за два периода.

Товар	Количество товара, тыс. ед.		Цена за единицу товара, руб.
	в базисном периоде	в отчётном периоде	в базисном периоде	в отчётном периоде
А	60	65	25,60	31,40
Б	52	64	65,38	84,10
В	62	78	30,25	28,20
Г	54	58	22,40	30,50
Д	48	48	67,50	68,40
Ж	35	32	80,00	88,20
З	64	68	33,00	35,10
К	42	46	62,00	65,50
Л	50	50	22,50	25,40
М	74	80	34,00	35,20
Н	28	34	57,0	60,40
П	42	30	110,0	180,40
Р	67	74	48,50	48,00
С	54	48	36,20	42,50
Т	38	42	24,40	25,50

Номера вариантов и исходные данные определяются по следующей таблице:

Варианты заданий:

№ варианта	№№ предприятий	№ варианта	№№ предприятий	15,2	20
1	А, Б, В	14	А, В, Д	18,4	25
2	Г, Д, Ж	15	Б, Г, Ж	12,0	8
3	З, К, Л	16	В, Д, З
4	М, Н, П	17	Г, Ж, К
5	Р, С, Т	18	Д, З, Л
6	Б, В, Г	19	Ж, К, М
7	В, Г, Д	20	З, Л, Н
8	Д, Ж, З	21	К, М, П
9	Ж, З, К	22	Л, Н, Р
10	К, Л, М	23	М, П, Т
11	Л, М, Н	24	А, Г, З
12	Н, П, Р	25	Б, Д, К
13	П, Р, С	-	-

Задача 2