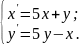5.Системи диференціальних рівнянь
Система рівнянь у вигляді
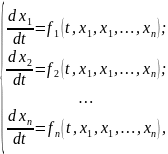(36)
де
t
— незалежна
змінна,
—
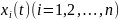шукані функції, називається нормальною
системою диференціальних рівнянь.
Розв'язком системи (36) є сукупність
функцій
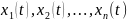,які задовольняють кожне з рівнянь цієї
системи.
Система
диференціальних рівнянь є лінійною,
якщо праві частини рівнянь (36) є
лінійними функціями відносно
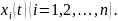
Існує
декілька методів розв'язування системи
лінійних диференціальних рівнянь.
Згідно з одним з них задана система
зводиться до диференціального рівняння
п
-го порядку відносно однієї з функцій
.
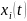Для цього обирають якесь рівняння
системи (36) і його послідовно диференціюють
п
раз, на кожному кроку виключаючи
похідні інших функцій
.
Приклад 14. Знайти частинний розв'язок системи диференціальних рівнянь
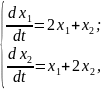
якщо
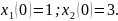
Розв'язування.
Диференціюємо
перше рівняння
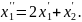
Підставимо
в це рівняння значення похідної
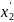із другого рівняння системи
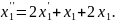
Знайшовши
з першого рівняння значення
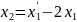i
підставивши його в знайдене рівняння,
дістаємо
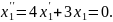
Маємо
лінійне однорідне рівняння другого
порядку зі сталими коефіцієнтами.
Його
розв'язок:
.
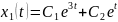Загальний
розв'язок для
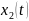знаходимо
із теперішнього рівняння системи:
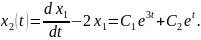
Використовуємо
задані початкові умови для знаходження
значень
:
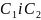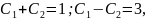звідси
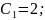
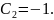
Таким
чином, частинний розв'язок системи:
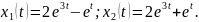
6.Розв'язування геометричних та фізичних задач
Теорію диференціальних рівнянь застосовують для розв'язування геометричних та фізичних задач. Розглянемо деякі з них.
Приклад 15. Знайти рівняння лінії, яка проходить через точку М(1;0) і для якої квадрат довжини відрізка, який визначається відстанню від початку координат до точки перетину з віссю ординат довільної дотичної, дорівнює добутку координат точки дотику.
Розв'язування.
На
шуканій лінії беремо довільну точку
М(х;у)
і
проводимо
дотичну
в цій точці NА
(рис. 1). За умовою прикладу
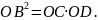
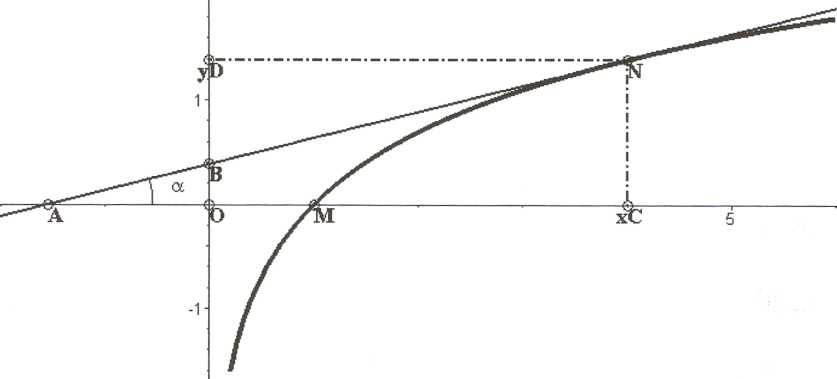
Рис.1
За
означенням похідної
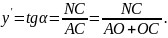
Враховуючи,що
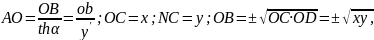
отримуємо
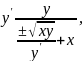або
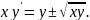
Дістали
однорідне диференціальне рівняння
першого порядку, тому що
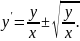
Знаходимо його розв'язок:
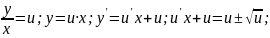
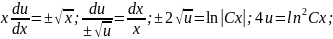
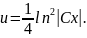
Загальний
розв'язок
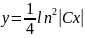таким чином дістали множину ліній, які
задовольняють умови прикладу. Із
цієї множини знаходимо певну криву, яка
проходить через точку М(1;0),
тобто частинний розв'язок рівняння,
який задовольняє початкову умову,
у(1)=
0.
Маємо
.
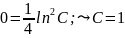Тоді рівняння шуканої лінії має вигляд
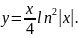
Приклад 16. Експериментально встановлено, що швидкість радіоактивного розпаду речовини пропорційна її кількості в даний момент часу. Знайти закон зміни маси речовини від часу, якщо при маса речовини дорівнювала m0.
Розв'язування. Нехай m=m(t) маса речовини в момент часу t. За умови
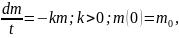
Де
k
-
коефіцієнт пропорційності. Знак мінус
береться тому, що з часом кількість
речовини
зменшується. Отримали диференціальне
рівняння з відокремлюваними змінними.
Розв’язуючи це рівняння, дістаємо, що
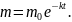
Варіанти індивідуальних завдань
Варіант 1
1.Знайти рівняння лінії, яка проходить через т. М0(16;1) і має таку властивість: вектор MN (N належить осі Oy, а М - довільна точка лінії), перпендикулярний дотичній до лінії в т. М, утворює гострий кут з додатним напрямом осі Оy і має довжину вектор |MN|= 20.
1.
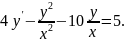
2.
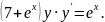
3.
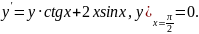
4.
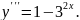
5.
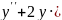
6.
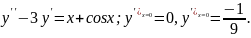
7.
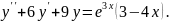
8.
9.
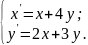
Варіант 2
1.Знайти рівняння лінії, яка проходить через точку (-2;3), якщо відрізок її нормалі, який міститься між осями координат, ділиться точкою дотику у відношенні 1:3.
2.
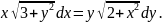
3.
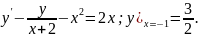
4.
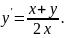
5.
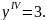
6.
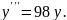
7.
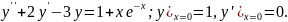
8.
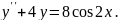
9.
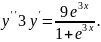
10.
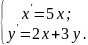
Варіант 3
1.Знайти рівняння лінії, що проходить через т. М(1;1) і має таку властивість, що кутовий коефіцієнт дотичної до будь-якої точки цієї лінії вдвічі більше кутового коефіцієнта прямої, яка з’єднує точку дотику і початок координат.
2.
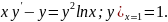
3.
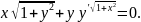
4.
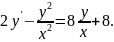
5.
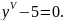
6.
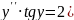
7.
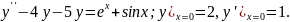
8.
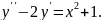
9.
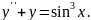
10.
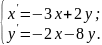
Варіант 4
1. Знайти лінію, що проходить через т. М(2;1), якщо відрізок дотичної, який міститься між осями координат, діліться точкою дотику у відношенні 1:2 (відраховуючи від осі Ох).
2.
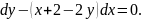
3.
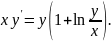
4.
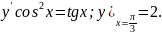
5.
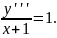
6.
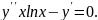
7.
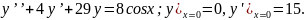
8.
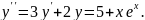
9.
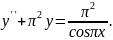
10.
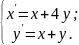
Варіант 5
1. Знайти рівняння лінії, у якої відрізок дотичної між осями координат, діляться навпіл у точці дотику. Лінія проходить через точку (2; 2).
2.
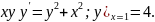
3.
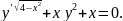
4.
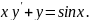
5.
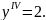
6.
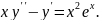
7.
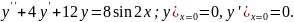
8.
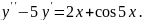
9.
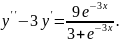
10.
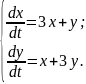
Варіант 6
1.Швидкість розпаду речовини пропорційна кількості x. Знайти залежність x від часу t, якщо після 1600 років залишається половина початкової (2кг) кількості речовини.
2.
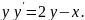
3.
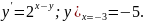
4.
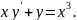
5.
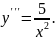
6.
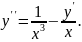
7.
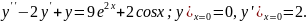
8.
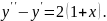
9.
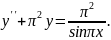
10.
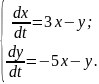
Варіант 7
1.Лінія
задовольняє рівняння
.
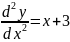Знайти
її рівняння, якщо відомо,що
лінія проходить через точку (2;4)
і в цій точці кутовий коефіцієнт дотичної
дорівнює 3.
2.
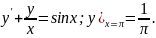
3.
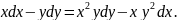
4.
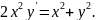
5.
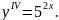
6.
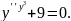
7.
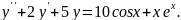
8.
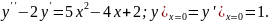
9.
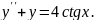
10.
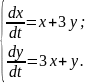
Варіант 8
1.Моторний човен рухається зі швидкістю 18 км/год. Через 5хв після виключення мотору його швидкість зменшилась до 6 км/год. Знайти відстань, яку пройшов човен по інерції до повної зупинки, якщо опір води пропорційний швидкості руху човна.
2.
3.
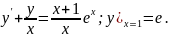
4.
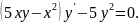
5.
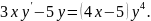
6.
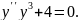
7.
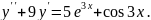
8.
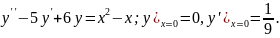
9.
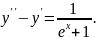
10.
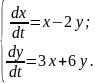
Варіант 9
1.Знайти рівняння кривої, що проходить через точку (1;2), якщо відрізок,який відсікається на осі ординат дотичною, дорівнює абсцисі точки дотику.
2.
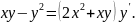
3.
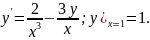
4.
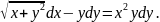
5.
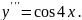
6.
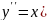
7.
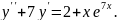
8.
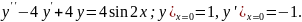
9.
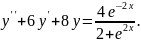
10.
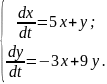
Варіант 10
1.Знайти рівняння кривої, що проходить через точку (1;0) і має таку властивість, що відрізок, який відзначається дотичною на осі Oу, дорівнює радіусу-вектору точки дотику.
2.
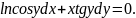
3.
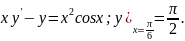
4.
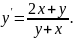
5.
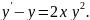
6.
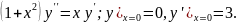
7.
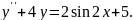
8.
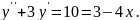
9.
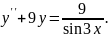
10.
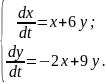
Варіант 11
1.Знайти рівняння кривої, що проходить через точку (-1 ;-1) і має таку властивість, що відрізок, який відзначається на осі Ох дотичною, дорівнює квадрату абсциси точки дотику.
2.
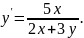
3.
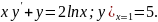
4.
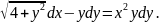
5.
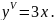
6.
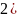
7.
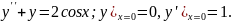
8.
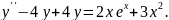
9.
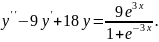
10.
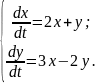
Варіант 12
1.Знайти криву, яка проходить через точку (3;4), якщо кутовий коефіцієнт дотичної в довільній точці кривої дорівнює квадрату ординати точки дотику.
2.
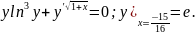
3.
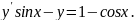
4.
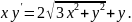
5.
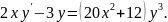
6.
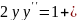
7.
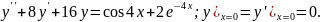
8.
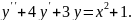
9.
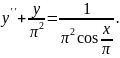
10.
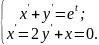
Варіант 13
1. Потяг рухається із швидкістю 60 км/год. Через 6хв після початку гальмування його швидкість стала 20 км/год. Скласти закон швидкості руху потягу, якщо сила гальмування пропорційна швидкості руху.
2.
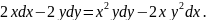
3.
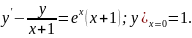
4.
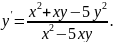
5.
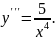
6.
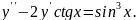
7.
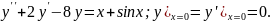
8.
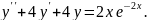
9.
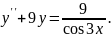
10.
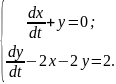
Варіант 14
1. Після виключення двигуна машина зупинилась через 30с. Визначити закон руху машини, якщо початкова швидкість її була 45 км/год, а сила опору руху пропорційна швидкості руху.
2.
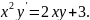
3.
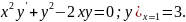
4.
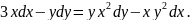
5.
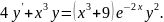
6.
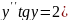
7.
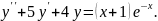
8.
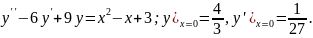
9.
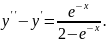
10.
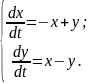
Варіант 15
1.Знайти сім’ю кривих, у яких всі нормалі проходять через початок координат.
2.
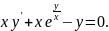
3.
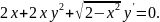
4.
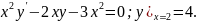
5.
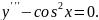
6.
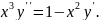
7.
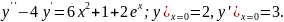
8.
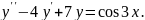
9.
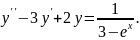
10.
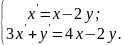
Варіант 16
1. Лінія проходить через точку (0;1). Відрізок будь-якої її нормалі, розташований між осями координат, ділиться точкою, до якої проведена нормаль, у відношенні 2:3. Знайти рівняння лінії.
2.
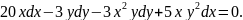
3.
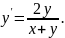
4.
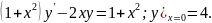
5.
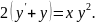
6.
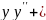
7.
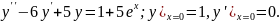
8.
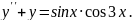
9.
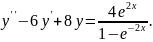
10.
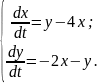
Варіант 17
1. Лінія проходить через точку М{2;1). Відрізок будь-якої її дотичної між точкою дотику і віссю Oу ділиться в точці перетину з віссю Ох у відношенні 1:2. Знайти рівняння лінії.
.
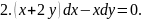
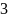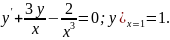
4.
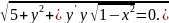
5.
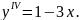
6.
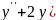
7.
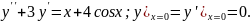
8.
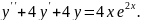
9.
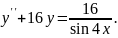
10.
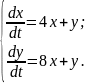
Варіант 18
1. За законом Ньютона швидкість охолодження тіла в повітрі пропорційна різниці між температурою тіла і температурою повітря. Якщо температура повітря дорівнює 20°С і тіло за годину охолоджується від 100 до 30°С, то через скільки хвилин (з початку охолодження) його температура знизиться до 60°С ?
2.
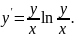
3.
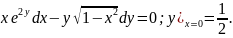
4.
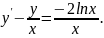
5.
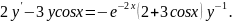
6.
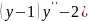
7.
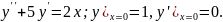
8.
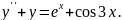
9.
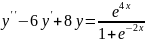
10.
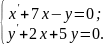
Варіант 19
1. Лінія проходить через точку М(-1;1). Відрізок будь-якої її дотичної між точкою дотику і віссю ординат ділиться точкою перетину з віссю абсцис у відношенні 3:1. Знайти рівняння лінії.
2.
3.
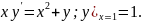
4.
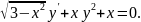
5.
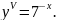
6.
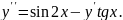
7.
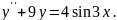
8.
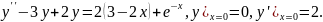
9.
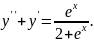
10.
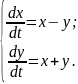
Варіант 20
1. Знайти рівняння лінії, яка проходить через точку М0(1;1) та має властивість таку, що кутовий коефіцієнт дотичної до будь-якої точки цієї лінії вдвічі більше кутового коефіцієнта прямої, яка поєднує точку дотику з початком координат.
2.
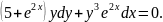
3.
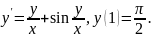
4.
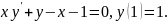
5.
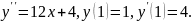
6.
7.
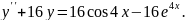
8.
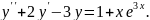
9.
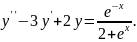
10.
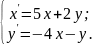
Варіант 21
1.
Знайти
рівняння кривої, яка проходить через
точку М(1;2),
якщо кутовий коефіцієнт дотичної до
будь-якої точки цієї кривої дорівнює
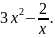
2.
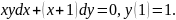
3.
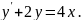
4.
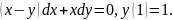
5.
6.
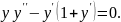
7.
8.
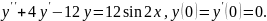
9.
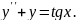
10.
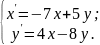
Варіант 22
1. Знайти криву, яка проходить через точку М(2;5), якщо відрізок будь-якої дотичної до цієї кривої, розташований між осями координат, поділяється точкою дотику навпіл.
2.
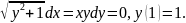
3.
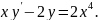
4.
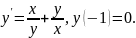
5.
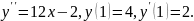
6.
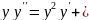
7.
8.
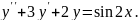
9.
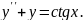
10.
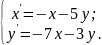
Варіант 23
1. Знайти криву, яка проходить через точку М(1;-1), якщо кутовий коефіцієнт дотичної у будь-якої точки М(х;у) на дві одиниці масштабу менше абсциси точки дотику.
2.
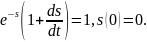
3.
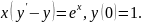
4.
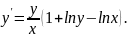
5.
6.
7.
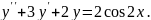
8.
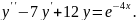
9.
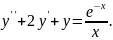
10.
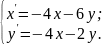
Варіант 24
1. Знайти рівняння кривої для якої трикутник, який утворюється віссю Oу, дотичною до кривої у будь-якій точці та радіусом-вектором точки дотику є рівнобічний (основою трикутника є відрізок дотичної від точки дотику до осі Oу).
2.
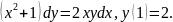
3.
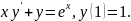
4.
5.
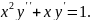
6.
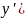
7.
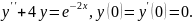
8.
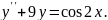
9.
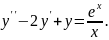
10.
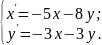
Варіант 25
1. Матеріальна точка масою 2г занурюється у рідину без початкової швидкості. Сила опору рідини пропорційна швидкості занурення, коефіцієнт пропорційності k = 2. Знайти залежність швидкості від часу. Знайти швидкість через 2с після початку занурення.
2.
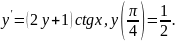
3.
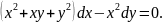
4.
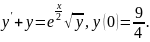
5.
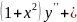
6.
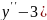
7.
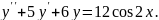
8.
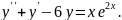
9.
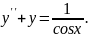
10.
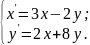
Варіант 26
1. Моторний човен рухається у спокійній воді зі швидкістю V = 12 км/год. На повному ходу його мотор був вимкнутий і через 10с швидкість човна зменшилася до V1= 6 км/год. Опір води пропорційний швидкості руху човна. Знайти швидкість човна через 1хв після зупинки мотора.
2.
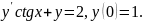
3.
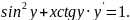
4.
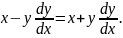
5.
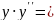
6.
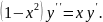
7.
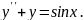
8.
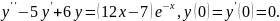
9.
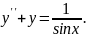
10.
Варіант 27
1. Крива проходить через точку М(2;-1) та має таку властивість, що кутовий коефіцієнт дотичної у будь-якій її точці пропорційний квадрату ординати точки дотику з коефіцієнтом пропорційності k = 3. Знайти рівняння кривої.
2.
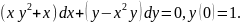
3.
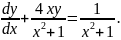
4.
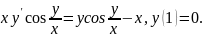
5.
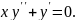
6.
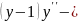
7.
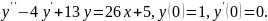
8.
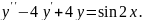
9.
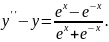
10.
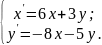
Варіант 28
1. Крива проходить через точку М(1;2) та має властивість, що добуток кутового коефіцієнта дотичної у будь-якій її точці на суму координат точки дотику дорівнює подвійній ординаті цієї точки. Знайти рівняння кривої.
2.
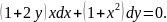
3.
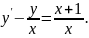
4.
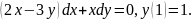
5.
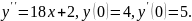
6.
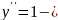
7.
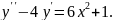
8.
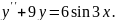
9.
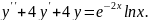
10.
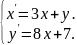
Варіант 29
1. Крива проходить через точку М(1;2) та має таку властивість, що відношення ординати будь-якої її точки до абсциси пропорційне кутовому коефіцієнту дотичної до кривої в цій же точці з коефіцієнтом пропорційності k = 3. Знайти рівняння кривої.
2.
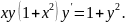
3.
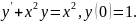
4.
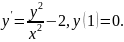
5.
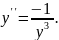
6.
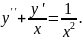
7.
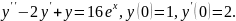
8.
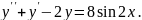
9.
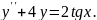
10.
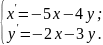
Варіант 30
1. Крива проходить через точку М(2;4) та має таку властивість, що відрізок який відсікається дотичною на осі Ох, проведеною у будь-якій точці кривої, дорівнює кубу абсциси точки дотику. Знайти рівняння кривої.
2.
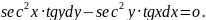
3.
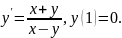
4.
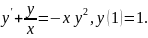
5.
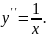
6.
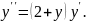
7.
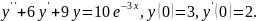
8.
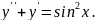
9.
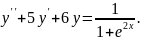
10.
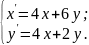
Варіант 31
1. Знайти криві, для яких площа трикутника, який утворюється оссю Ох, дотичною та радіусом-вектором точки дотику, дорівнює 4.
2.
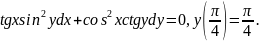
3.
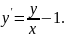
4.
5.
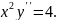
6.
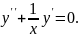
7.
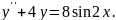
8.
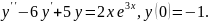
9.
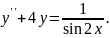
10.
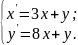
Варіант 32
1. Знайти криву, у кожній точці якої дотична перпендикулярна до радіуса-вектора точки дотику.
2.
.
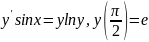3.
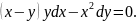
4.
5.
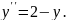
6.
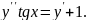
7.
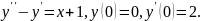
8.
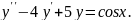
9.
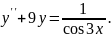
10.
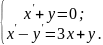
Варіант 33
1. Знайти рівняння руху тіла, якщо воно рухається прямолінійно з прискоренням а = 2м/с2 . До моменту початку відліку (t = 0) тіло рухалось зі швидкістю 7 м/с та пройшло шлях 24м. Знайти шлях тіла за 15с.
2.
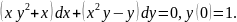
3.
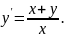
4.
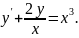
5.
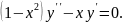
6.
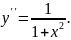
7.
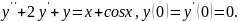
8.
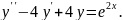
9.
10.
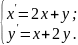
Варіант 34
1. Знайти рівняння кривої, яка проходить через точку М(1;1) та має таку властивість, що кутовий коефіцієнт дотичної у будь-якій точці М кривої вдвічі більше кутового коефіцієнта радіуса-вектора точки М.
2.
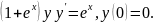
3.
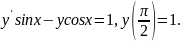
4.
5.
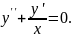
6.
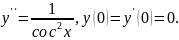
7.
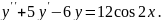
8.
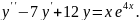
9.
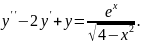
10.
Варіант 35
1. Знайти криву яка проходить через точку М(-1;4) та має таку властивість, що проекція відрізка нормалі між віссю Ох і точкою дотику на вісь Ох має постійне значення, яке дорівнює 4.
2.
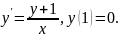
3.
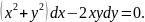
4.
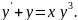
5.
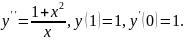
6.
7.
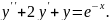
8.
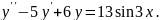
9.
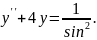
10.
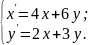
Варіант 36
1. Матеріальна точка рухається по прямій зі швидкістю, зворотно пропорційною пройденому шляху. У початковий момент руху точка знаходилась на відстані 5м від початку відліку та мала швидкість Y0 = 20 м/с. Визначити пройдений шлях та швидкість точки через 10с після початку руху.
2.
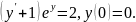
3.
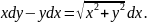
4.
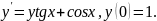
5.
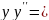
6.
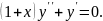
7.
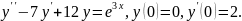
8.
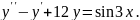
9.
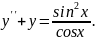
10.
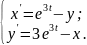
Варіант 37
1. Човен уповільнює свій рух під дією опору води, який пропорційний швидкості човна. Початкова швидкість човна дорівнює 2 м/с, а його швидкість через 4с дорівнює 1 м/с. Через скільки секунд швидкість човна дорівнюватиме 0,25 м/с? Який шлях може пройти човен до зупинки?
2.
3.
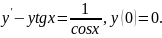
4.
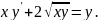
5.
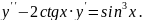
6.
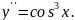
7.
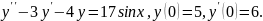
8.
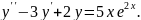
9.
10.
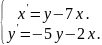
Варіант 38
1. Знайти рівняння кривої, яка проходить через точку М{4;4) та має таку властивість, що відрізок будь-якої дотичної, розташований між точкою дотику та віссю Ох, поділяється віссю Oу навпіл.
2.
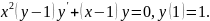
3.
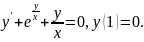
4.
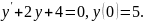
5.
6.
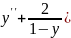
7.
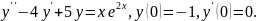
8.
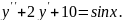
9.
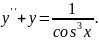
10.
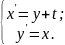
Варіант 39
1. Знайти рівняння руху тіла, якщо його швидкість пропорційна пройденому шляху і тіло проходить 100м за 10с, а 200м за 15с.
2.
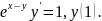
3.
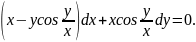
4.
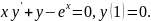
5.
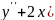
6.
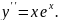
7.
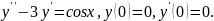
8.
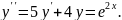
9.
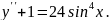
10.
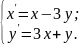
Варіант 40
1. Знайти рівняння кривої, яка проходить через точку М(9;9) та має таку властивість, що кутовий коефіцієнт будь-якої дотичної вдвічі менше кутового коефіцієнта радіуса-вектора точки М.
2.
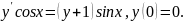
3.
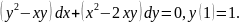
4.
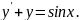
5.
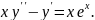
6.
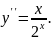
7.
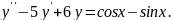
8.
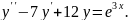
9.
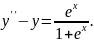
10.