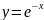2.4.Рівняння Бернуллі

Нелінійне диференціальне рівняння першого порядку, яке має вигляд

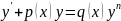(18)

де n ≠ 0; n ≠ 1, називається рівнянням Бернуллі (ліва частина цього рівняння збігається з лівою частиною лінійного рівняння). Рівняння Бернуллі за допо­могою заміни 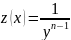перетворюється до лінійного рівняння відносно функції z(х). Але на практиці доцільно це рівняння зразу розв'язувати за до­помогою заміни (14).

Приклади розв'язування диференціальних рівнянь першого порядку

Приклад 1. Знайти загальний розв'язок рівняння

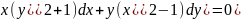
Розв'язування. Визначаємо, що маємо диференціальне рівняння з відокремлюваними змінними(нагадує вираз(7)). Зводимо рівняння до вигляду (6):

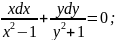
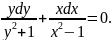
Інтегруємо отриману рівність:

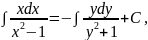
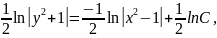
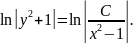
У цьому прикладі доцільно було довільно сталу С замінити на .

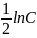Далі отримуємо 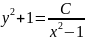,звідки загальний розв'язок приймає вигляд

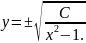
Приклад 2. Знайти частинний розв'язок рівняння 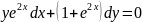коли .

Розв'язування. Маємо рівняння з відокремлюваними змінними. Ділимо рівняння на 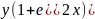,отримуємо .

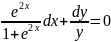Інтегруємо цей вираз і визначаємо:

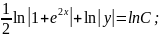
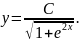
Підставляємо початкову умову в отриманий загальний розв'язок:

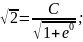C = 2.

Частинний розв'язок приймає вигляд

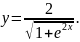
Приклад 3. Розв'язати рівняння

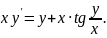
Розв'язування. Шляхом ділення рівняння на змінну х отримуємо однорідне ди­ференціальне рівняння (похідна залежить від відношення ):

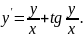
Робимо заміну:

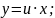
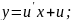
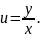
Підставляємо ці значення у задане рівняння і розв'язуємо отримане диференці­альне рівняння з відокремлюваними змінними:

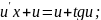
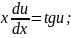
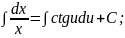
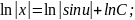
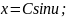
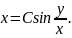
Отримали загальний інтеграл рівняння.

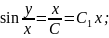
Звідси 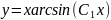— загальний розв'язок.

Приклад 4. Знайти загальний розв'язок рівняння

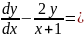
Розв'язування. Визначаємо, що маємо лінійне диференціальне рівняння (13). Робимо заміну

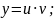
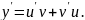
Після підстановки отримуємо:

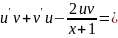
Послідовно розв'язуємо наступні два рівняння:

1)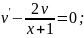 2)

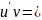
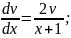
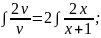
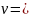
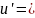
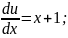
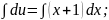
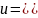
Загальний розв'язок рівняння:

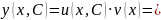
Приклад 5. Знайти розв’язок задачі Коші

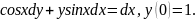
Розв'язування. Поділивши обидві частини рівняння на добуток 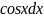, отри­муємо лінійне диференціальне рівняння:

Робимо заміну:

Маємо

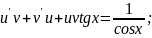
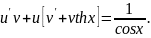
1)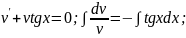 2)

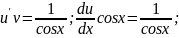
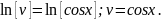
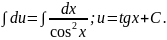
Загальний розв'язок:

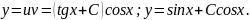
Знайдемо значення сталої C, при якому частинний розв'язок задовольняє поча­ткову умову:

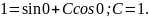
Частинний розв’язок:

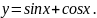
Приклад 6. Розв’язати рівняння

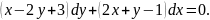
Розв'язування. Враховуючи ,що рівняння приводимо до (12):

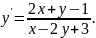
Визначаємо, що

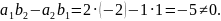
Знаходимо точку перетину прямих:

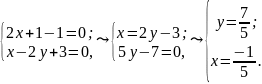
Маємо

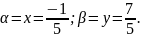
Робимо заміну

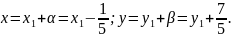
Тоді і задане рівняння приймає вигляд

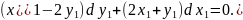
Отримали однорідне диференціальне рівняння. Покладаємо:

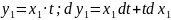
Розв'язуємо отримане рівняння з відокремлюваними змінними:

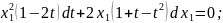
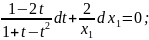
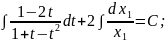
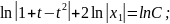
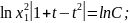
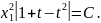
Підставляючи значення t,x₁,y₁ дістаємо загальний розв'язок рівняння:

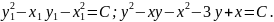
3.Диференціальні рівняння вищих порядків метод зниження порядку

3.1.Рівняння y⁽ⁿ⁾ = (x)розв'язується шляхом інтегрування п разів по­слідовно:

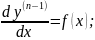
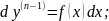
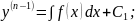
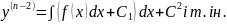
3.2.Рівняння 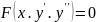,тобто рівняння другого порядку, яке не має змінної y, розв'язують шляхом зниження його порядку за допомогою заміни 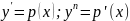.Отримуємо рівняння першого порядку відносно змін­них р і х. Знаходимо його розв'язок 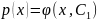і потім шукану функцію у(х) шляхом його інтегрування:

.

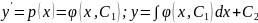3.3.Рівняння другого порядку, в якому відсутня змінна х, тобто рів­няння по аналогії розв'язують за допомогою заміни:

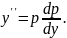
Приклад 7. Знайти загальний розв'язок рівняння у^m - х- sin2x.

Розв'язування. Маємо рівняння третього порядку, яке приводимо до вигляду 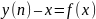і потім тричі послідовно інтегруємо:

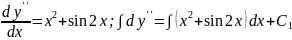
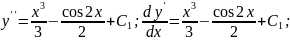
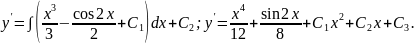
Приклад 8. Розв'язати рівняння

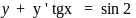
Розв’язування. Це рівняння другого порядку, в якому відсутня змінна у . Зни­жуємо його порядок за допомогою підстановки y' = р(х); у" = р’(х). Одержуємо лі­нійне рівняння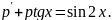

Розв'язок цього рівняння шукаємо у вигляді p = u - v.

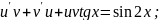
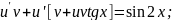
1)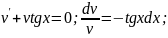 2)

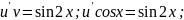
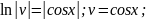
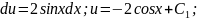
Повертаючись до змінної у, отримуємо рівняння

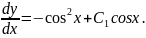
Його розв'язок після інтегрування:

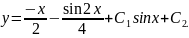
Приклад 9. Знайти частинний розв'язок рівняння 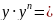, який задо­вольняє умовам: y(0) = 1; y’(0) = -1.

Розв'язування. Рівняння другого порядку, яке не має змінної х. Поклавши 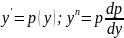після підстановки дістанемо диференціальне рівняння з відо­кремлюваними змінними

1)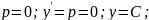 2)

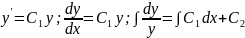
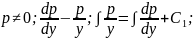
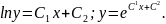
Знайшли загальний розв'язок рівняння. Для знаходження частинного розв'язку треба визначити значення С₁ і С₂ на основі початкових умов. Маємо:

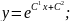
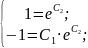
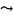
Частинний розв'язок рівняння приймає вигляд