
- •План самостійного вивчення студентами навчального матеріалу з курсу
- •Для спеціальності 5.080405 “Розробка програмного забезпечення”
- •Література
- •1.Загальні означення
- •2.Диференціальні рівняння першого порядку
- •2.1.Диференціальні рівняння з відокремленими і відокремлюваними змінними
- •2.2.Однорідні рівняння
- •2.3.Лінійні диференціальні рівняння
- •2.4.Рівняння Бернуллі
- •3.Диференціальні рівняння вищих порядків метод зниження порядку
- •4.1.Лінійні однорідні диференціальні рівняння із сталими коефіцієнтами
- •4.2.Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •4.2.1.Метод невизначених коефіцієнтів
- •4.2.2.Метод варіації довільних сталих
- •5.Системи диференціальних рівнянь
- •6.Розв'язування геометричних та фізичних задач
- •Варіанти індивідуальних завдань
- •Література
2.2.Однорідні рівняння
Функція f(x; у) називається однорідною п -го виміру, якщо має місце тотожність при будь-якому значенні λ :
f(λx,λy) = λn · f(x,y)
Наприклад,
функція
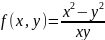 є однорідною нульового виміру, тому
що
є однорідною нульового виміру, тому
що
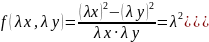
Рівняння у’ = f{x,у) є однорідним диференціальним рівнянням першого порядку, якщо f(х,у) - однорідна функція нульового виміру.
Довільне
однорідне диференціальне рівняння
можна перетворити до виразу
тобто
похідну визначити як функцію відношення
змінних

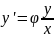 (9)
(9)
Однорідні диференціальні рівняння розв'язують за допомогою заміни
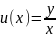 ,
(10)
,
(10)
звідки
y = u · x; y’ = u’ · x +u. (11)
Вирази (11) підставляють у рівність (9) і отримують рівняння з відокремлюваними змінними відносно и(х) і x.
Рівняння вигляду M(x,y)dx +N(x,y)dy = 0 буде однорідним, якщо М(x,у) і N(x,y) - однорідні функції однакового виміру, наприклад:
(2х + 3y)dx + (х - 2y)dy = 0,
(х2 + у2 )dx - 2xydy.
До однорідного диференціального рівняння зводиться рівняння, яке має вигляд:
y’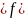 )
(12)
)
(12)
Якщо a1b2 – a2b1 = 0 ,рівність (12) перетворюють до однорідного рівняння (9) за допомогою заміни x= x1 + α; y1 + β, де (α,β) – точка перетину прямих і a1x + b1y + c1 = 0 і a2x + b2y + c2 = 0.
Коли a1b2 – a2b1 = 0 , то підстановка a1x + b1y = t дозволяє отримати рівняння з відокремлюваними змінними.
2.3.Лінійні диференціальні рівняння
Рівняння
y’ + p(x) · y = q(x), (13)
в якому невідома функція у і її похідна y’ входять до рівняння у першому степеню і не множаться між собою, називається лінійним диференціальним рівнянням першого порядку.
Розв'язок у(х) цього рівняння шукають у вигляді добутку двох невідомих функцій и(х) і v(x), тобто
y = u · v. (14)
Тоді похідна функції приймає вигляд
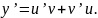 (15)
(15)
Значення у(х) і y’ підставляють у рівняння (13) і отримують вираз:
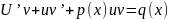 (16)
(16)
або
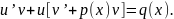 (17)
(17)
Функцію v визначають із умови, що вираз в дужках дорівнює нулю, тобто розв'язують рівняння, яке буде завжди з відокремлюваними змінними:
v
+ p(x)v = 0;
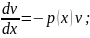
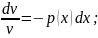
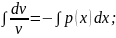
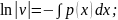
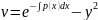 (C =
0).
(C =
0).
Потім
значення v
підставляють
у рівняння
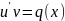 і з отриманого диференціального рівняння
теж з відокремлюваними змінними знаходять
загальний
розв'язок
і з отриманого диференціального рівняння
теж з відокремлюваними змінними знаходять
загальний
розв'язок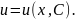 Значення V
і и
підставляють у рівність (14) і визначають
загальний розв'язок лінійного
диференціального рівняння.
Значення V
і и
підставляють у рівність (14) і визначають
загальний розв'язок лінійного
диференціального рівняння.
