1.1.2. Пластинчатый конечный элемент

В общем случае в качестве пластинчатых конечных элементов выступают трех- и четырехугольные пластины, работающие как на изгиб, так и на растяжение/сжатие в плоскости. На рис. 1.2 изображен треугольный пластинчатый конечный элемент.

Пластинчатый конечный элемент, также как и стержневой, считается тон­ким, так что изгиб пластинчатого элемента описывается гипотезой Кирхгофа [3,4]. На практике это означает, что толщина моделируемой пластинчатой конструкции должна быть не менее чем в пять раз меньше ее максимального линейного размера.

Каждый из узлов такого конечного элемента имеет пять степеней свободы. три поступательных перемещения и два изгибающих поворота вокруг осей X и Y. На рис. 1.2 показаны

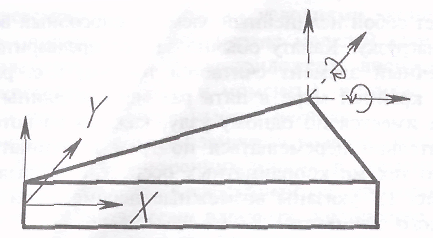
Рис. 1.2. Внешний вид изгибаемого пластинчатого треугольного конечного элемента

перемещения и повороты вокруг осей X и Y для одного из узлов.

Для того чтобы матрица жесткости ансамбля не вырождалась, в узлы пластинчатого конечного элемента добавляется фиктивная жесткость — поворот вокруг оси Z. Таким образом, в дальнейшем можем считать, что каждый узел пластинчатого конечного элемента, также как и у стержня, имеет шесть степеней свободы.

1.1.3. Объемные (сплошные) конечные элементы

Наиболее распространенными формами объемных конечных элементов являются четырехузловой тетраэдр, шестиузловая треугольная призма и восьмиузловой гексаэдр (рис. 1,3—1,4).

С точки зрения точности расчета наилучшей будет модель, подвергнутая разбиению на восьмиузловые конечные элементы, хотя погрешность вычислений при применении других типов конечных элементов не превышает допустимые МКЭ нормы. Кроме того, следует иметь в виду, что генераторы разбиения трехмерной области на конечные элементы большинства имеющихся на сегодняшний день конечно-элементных пакетов производят разбиение таких областей на тэтраэдрические элементы. Во входящем в состав АРМ WinMachine редакторе

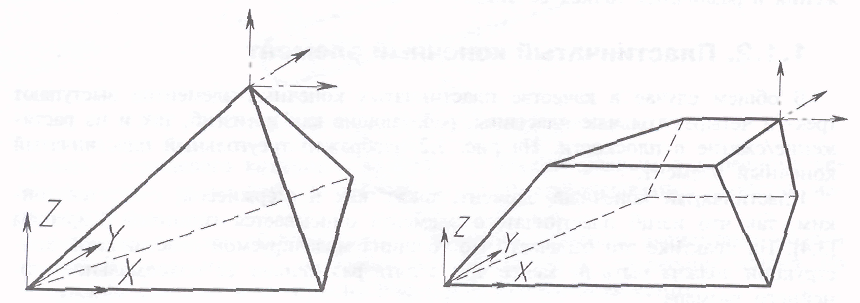
Рис. 1.3. Объемный четырехузловой Рис.1.4. Объемный восьмиузловой

конечный элемент в виде тетраэдра конечный элемент в виде гексаэдра

трехмерных моделей АРМ Studio, с помощью которого модель конструкции создается и готовится к расчету, также предусмотрено разбиение на четырехузловые тэтраэдрические элементы.

С помощью объемных элементов моделируются конструкции (или их составные части), имеющие соизмеримые размеры по различным координатам, т. е. которые не могут быть адекватно описаны стержневыми и пластинчатыми конечными элементами.

Каждый узел объемного конечного элемента обладает только тремя поступательными степенями свободы, вращательные степени свободы отсутствуют. Тогда количество строк (и столбцов) матрицы жесткости модели, состоящей только из объемных конечных элементов, равно числу узлов, умноженному на три.

Поскольку узлы объемных конечных элементов имеют только три степени свободы, то их можно рассматривать как сферические шарниры, которые сводят к нулю все приложенные внешние моменты. Значит, каждый конечный элемент передает соседним элементам только усилия и линейные перемещения, но не момент и угол поворота. Поэтому задавать силовые факторы в узлах объемного конечного элемента в виде моментов не следует, даже если программа формально позволяет это сделать — при расчете они все равно будут проигнорированы.

Если все же возникает необходимость в приложении внешних моментов, то их можно задавать в виде некоторой пары сил, линии действия которых проходят через узлы конечных элементов.

Эту же особенность узлов объемных конечных элементов нужно учитывать при формировании соединения объемных конечных элементов со стержневыми или пластинчатыми.

Довольно важным является вопрос о выборе тех или иных типов конечных элементов при моделировании конструкции, тем более что иногда этот выбор далеко не очевиден. Часто бывает, что одна и та же конструкция может быть смоделирована различными типами элементов, например, и пластинчатыми, и объемными. Если моделируемый объект достаточно «толстый», то в этом случае от использования объемных конечных элементов можно ожидать большей точности, поскольку у них отсутствуют ограничения, связанные с соотношением толщины и других размеров. С другой стороны, моделирование тонкого объекта пластинчатыми элементами позволит повысить точность расчета за счет того, что узлы пластины имеют шесть степеней свободы против трех в объем­ных элементах. Поэтому дать однозначный совет, какие типы элементов пред­почтительнее использовать в каждом конкретном случае, весьма затруднительно, да и критерии такой оптимизации могут быть различными. Некоторые общие рекомендации сформулированы выше, но выбор остается за пользователем.