9.3. Деформационный расчет

Деформационный расчет называют также геометрически нелинейным расче­том или расчетом с учетом осевых составляющих нагрузок. Как правило, он дает более точные результаты по сравнению со статическим расчетом. Дело в том, что статический расчет имеет одну особенность — перемещения элемен­тов модели считаются малыми, и дополнительные силовые факторы, возни­кающие вследствие таких перемещений, не учитываются.

Возникновение дополнительных силовых факторов поясним на примере. Рассмотрим вертикальный стержень, в нижнем узле которого имеется опора в виде заделки, а к верхнему узлу приложена произвольная сила F (рис. 9.8). Под действием этой силы произойдет смещение верхней части стержня на ве­личину 5 в горизонтальной плоскости. Точка приложения силы F тоже сме-

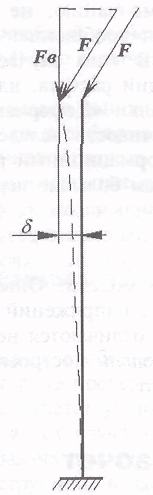
Рис. 9.8. К пояснению сути деформационного расчета

шается на величину 5, и у вертикальной составляющей этой силы f_b появля­ется дополнительный изгибающий момент относительно точки опоры, рав­ный |F_Ex5|. При статическом расчете такой момент не учитывался, его учет воз­можен только при проведении деформационного расчета.

Деформационный расчет не может выполняться одновременно со статичес­ким, поскольку эти типы расчетов используют одни и те же инструменты для визуализации результатов. Однако при проведении деформационного расчета автоматически происходит и расчет на устойчивость с учетом геометрической нелинейности и больших перемещений. Несмотря на то, что опция «Устой­чивость» диалогового окна «Расчет» неактивна, результаты анализа устойчн-

вости конструкции доступны для просмотра, о чем свидетельствует активный пункт «Устойчивость» в меню «Результаты».

Параметры деформационного расчета можно задать в полях ввода вкладки «Деформационный расчет» диалогового окна «Установки» (см. рис. 9.4). В дан­ном случае задаем только «Точность деформационного расчета» и «Максималь­ное количество итераций деформационного расчета». По умолчанию эти вели­чины равны 0,0001 и 20 соответственно.

Просмотр результатов деформационного расчета аналогичен просмотру ре­зультатов статического расчета (см. главу 3) и расчета на устойчивость (см. п. 9.2.3). Здесь подчеркнем только некоторые особенности деформационно­го расчета.

• Деформационный расчет, также как и расчет на устойчивость, прово­ дится итерационным методом при заданном максимальном числе итера­ ций и определенной точности. Если в результате выполнения 20 итера­ ций, установленных по умолчанию, не будет достигнута заданная точ­ ность расчета, то появится сообщение: «Количество итераций превысило максимально допустимое». В этом случае следует или увеличить макси­ мальное количество итераций расчета, или уменьшить его точность в со­ ответствующих полях вкладки «Деформационный расчет».

• Если модель теряет устойчивость вследствие действия на нее слишком больших нагрузок, то деформационный расчет сходиться не будет, и по­ явится сообщение «Слишком большие перемещения». В этом случае вели­ чины действующих на модель силовых факторов нужно уменьшить.

• В большинстве случаев из сравнения результатов деформационного и ста­ тического расчетов можно сделать вывод о корректности и работоспо­ собности рассматриваемой модели. Опыт показывает, что если резуль­ таты расчета максимальных напряжений при проведении статического и деформационного расчетов отличаются не более чем на 2-5-3%, то это сви­ детельствует о том, что модель построена грамотно и будет вполне ра­ ботоспособной, и наоборот.