8.2.1. Задание действующих на стержни распределенных нагрузок в глобальной системе координат

В п. 2.4.4.3 задание распределенных нагрузок на стержни в локальной системе координат стержня иллюстрировалось примером конструкции, модель которой изображена на рис. 2.5. При этом все стержни модели были параллельны и имели одинаковую ориентацию собственных локальных систем координат. На практике, однако, гораздо чаще встречается более сложная задача: стержни непараллельны, их локальные системы координат (после установки требуемой ориентации поперечных сечений) различны, а вот направление действующей на них нагрузки одинаково.

Если распределенную нагрузку задавать описанным в п. 2.4.4.3 способом, то для каждого из стержней придется вычислить проекции нагрузки на оси соответствующей локальной системы координат. Это весьма неудобно и требует выполнения значительных по объему вспомогательных расчетов.

Для упрощения решения такой задачи в АРМ Structure3D предусмотрен режим задания распределенных нагрузок на стержень в глобальной системе координат. Этот инструмент позволяет задать распределенную нагрузку, действующую на один стержень или группу стержней, и разложить ее по осям локальной системы координат каждого стержня,

В качестве примера рассмотрим пирамиду, на стержни боковых ребер которой в направлении сверху вниз действует вертикальная распределенная нагрузка определенной интенсивности. Прежде чем задавать действующую нагрузку, посмотрим, как расположены локальные системы координат стерж-

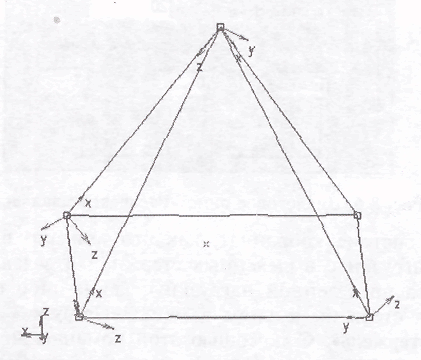
Рис. 8.5. Модель пирамиды с показом локальной системы координат каждого из ребер

ней. Для этого следует сначала выделить нужную группу стержней, а потом воспользоваться режимом «Ориентация сечения» (см. п. 2.4.2.4). На рис. 8.5 видно, что в данном случае и сами стержни, и их локальные системы координат ориентированы произвольным образом.

Далее действуем стандартно: выделяем те элементы, на которые действует распределенная нагрузка, выбираем в меню «Нагрузки» пункт «Глобальная на стержень» и в появившемся диалоговом окне «Распределенная сила» (рис. 8.6) задаем значение этой силы и ее направление в глобальной системе координат.

Направление действия силы задается вектором с координатами (X,Y,Z), величины которых записываются в соответствующие поля ввода. Поскольку по условию к боковым ребрам нужно приложить вертикальную силу, действующую сверху вниз, т. е. противоположно положительному направлению оси Z, то в поле «Z:» достаточно ввести любое отрицательное число. Если направление действия вектора внешней силы будет произвольно, то должны быть введены соответствующие значения его проекций на другие оси.

Значение силы также может быть как положительным (если вектор силы коллинеарен заданному), так и отрицательным.

После нажатия кнопки «ОК» к выделенным стержням будет приложена распределенная сила, действующая в заданном направлении, но разложенная по осям локальной системы координат каждого стержня (рис. 8.7). Обратите внимание, что рассматриваемая нагрузка имеет проекции по трем направлен» локальной системы координат: осевому и двум поперечным.

Редактировать введенную таким образом нагрузку можно двумя способами: или работая с каждой отдельной составляющей каждого отдельного стер-

Рис. 8.6. Диалоговое окно «Распределенная сила»

жня в локальной системе координат, как это описано в главе 2, или удаляя распределенные нагрузки с выделенных стержней и задавая новые.

Для удаления распределенной нагрузки с каких-либо стержней нужно вначале выделить эти стержни, а затем в меню «Нагрузки» выбрать пункт «Удалить нагрузки на стержень». С помощью этой команды могут быть удалены все нагрузки, действующие в локальной системе координат всех выделенных стер-

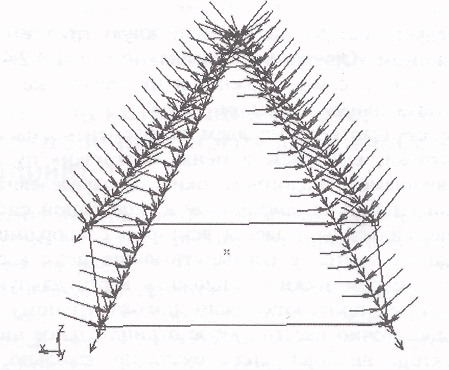
Рис. 8.7. Распределенная сила в глобальной системе координат

жней. Перед удалением программа задаст вопрос Следует ли удалять нагрузки только из активного загружения? При положительном ответе нагрузки будут удалены только из активного загружения, при отрицательном — из всех.