5. Правило симпсона
Сложные эпюры надо разбивать на простые, у которых известны площади и положения центров тяжести. Однако такой подход вызывает затруднения при расчетах, поэтому здесь лучше применять правило Симпсона:
![]()
Здесь l – длина участка; а, b, с, d – крайние, h, e – средние ординаты обеих эпюр. Произведения ас, he, bd принимаются положительными, если обе парные ординаты имеют один знак, отрицательными, – если разные знаки.
Формула Симпсона дает точный результат как для случая «сопряжения» двух прямолинейных эпюр (рис., а), так и для случая «сопряжения» квадратной параболы с прямой (рис., б).
Cредние ординаты на прямолинейных участках эпюр легко находятся как полусуммы крайних ординат, а на криволинейных участках средние ординаты должны быть вычислены по уравнениям квадратной параболы.

К правилу Верещагина
Таблица 1
Формулы для определения площадей эпюр
и положений их центров тяжести
Нагружение |
Вид эпюры изгибающего момента |
zc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Парабола (квадратная) с вершиной в т.А
|
|
|
|
Парабола (квадратная)
|
|
|
|
Парабола (кубическая) с вершиной в т.А
|
|
|
|
Парабола (кубическая) с вершиной в т.А
|
|
|
|
Парабола (квадратная) с вершиной в т.А
|
|
|
Таблица 2
Внимание!
Эпюры М в табл. 2 и табл. 4 необходимо зеркально перевернуть
(они построены по - машиностроительному, а не по - строительному)

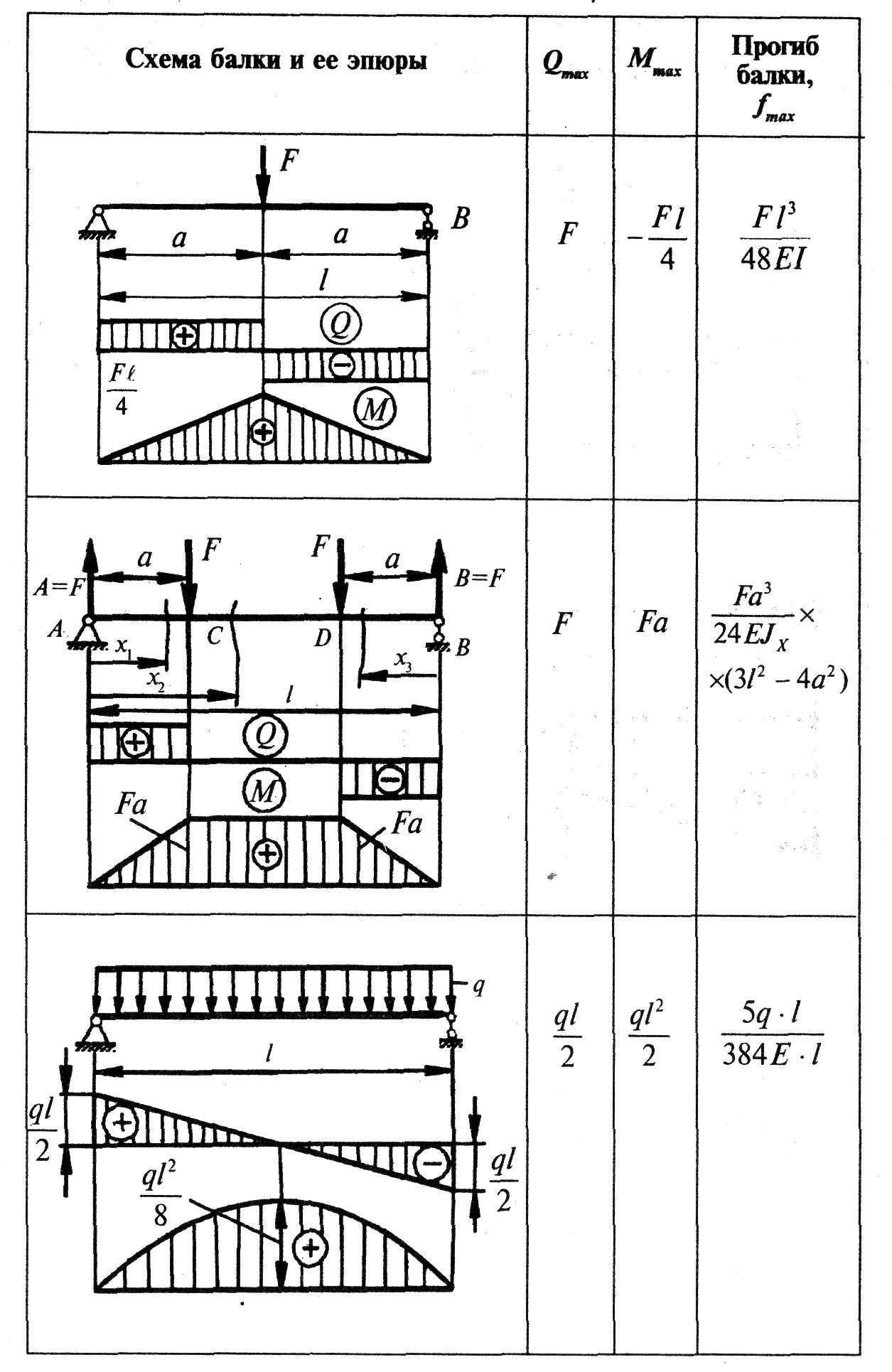
В схемах, показанных в табл. 2, ω означает площадь эпюры моментов, а f - наибольший изгибающий момент на соответствующей эпюре моментов.
Таблица 3
Формулы для определения прогибов и углов
поворотов характерных сечений балки

Таблица 4
Эпюры и перемещения балки
Fl3/3EJ