2. Оценка достоверности модели и статистической значимости параметров

Для проверки правильности полученных результатов применяем стандартную функцию «ЛИНЕЙН».

0,73949 0,263614 0,408791 0,027077 0,02825 0,019127 0,999897 0,004084 #Н/Д 33908,72 7 #Н/Д 1,13132 0,000117 #Н/Д

Далее находим оцененный коэффициент детерминации. Оцененный коэффициент детерминации – это коэффициент, у которого соответствующие суммы квадратов скорректированы по их степени свободы.

_

R² = 1 – (1 – R²) (2.1)

По этой формуле находим оцененный коэффициент детерминации и он составит 0,999867.

Для проверки адекватности многофакторной регрессионной модели используется F–критерий Фишера. При этом базовая гипотеза статистики имеет вид H0: β1 = β2 =…= βm = 0 против альтернативной гипотезы H1: хотя бы одно значение βi отлично от нуля.

Используя функцию в Excel «FРАСПОБР», находим F критическое, оно составит 4,74 – модель адекватна.

Для оценки статистической значимости параметров многофакторной регрессии следует построить t–статистику для каждого из параметров.

(2.2)

t0 =	21,37291
t1 =	9,331293
t2 =	27,31013

По встроенной в excel функции СТЬЮДРАСПОБР находим t критическое.

t kp =

2,364624

По этому можно сделать вывод что все параметры многофакторной регрессии статистически значимые.

Для того чтобы определить, как найденные оценки параметров многофакторной регрессии связаны с параметрами классической регрессии, необходимо построить интервалы доверия для параметров линейной и степенной моделей:

β_i = b_i + t_α/2σ_bi (2.3)

1,45977	<=β0<= 1,550225
1,234823	<=β1<= 1,368427
2,030839	<=β2<= 2,158895

3. Прогнозирование экономических показателей по модели многофакторной регрессии

Если построенная модель адекватна реальной действительности, то ее можно использовать для прогнозирования зависимой переменной модели, т.е. для прогнозирования объема выпуска продукции.

Точечный прогноз для модели выпуска продукции (линейной и степенной) на плановый период, указанный в исходных данных, т.е. в (n + k)–период определяется по формуле:

_^

Y_n+k = A₀+a₁x_1,n+k+a₂x_2,n+k (3.1)

Таким образом y_пр для линейной функции составит 33,86643701.

А y_пр для степенной –31,89995

.

П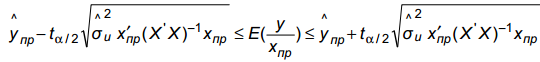 остроение интервалов доверия для математического ожидания объема выпуска продукции выполняется так:

(3.2)

где x' _пр = {1;x_1,пр; x_2,пр }

Таким образом, получим интервалы доверия для математического ожидания:

33,77505

<= E(Ypr) <=

33,95781921

Интервальный прогноз для определения объема выпуска продукции на плановый период для линейной и степенной моделей определяют по формуле:

(3.3)

Рассчитав его в excel, получим:

22,65748

<= Y pr <=

45,07539282

Далее находим ошибку прогноза для линейной и степенной моделей.

Для этого оценим сначала:

– среднеарифметическую абсолютную ошибку прогноза для линейной и степенной моделей:

(3.3)

где

– среднеквадратичную ошибку прогноза для линейной и степенной моделей:

MSE = ((u8)²+(u9)²+(u10)²)/3; (3.4)

– относительную ошибку прогноза для линейной и степенной моделей:

(3.5)

– коэффициент несоответствия Тейла для линейной и степенной моделей:

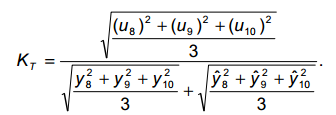(3.6)

Рассчитав по данным формулам показатели получаем, что:

MAE =0,02

MSE = 0,0005

MAPE = 0,045

Кт = 0,0007

Можно сделать выводы, что точность прогноза отличная.

Вычислим отношение ожидаемого уровня выпуска продукции, полученного на базе линейной и степенной моделей:

Eпр = Yпр.ст-Yпр.лн (3.7)

Получим Eпр = -1,97