Решение

Ёмкостное сопротивление x_С = = = 39,81 Ом.

Амплитудное значение напряжения на ёмкости

u_Cm = I_m x_C = 1039,81 = 398,1 B.

Действующие значения

I = = = 7,07 A, u_C = = = 281,5 B.

Действующие значения напряжений на активных сопротивлениях

u_r1= I r₁ = 7,0710 = 70,7 B, u_r2= I r₂ = 7,0720 = 141,4 B.

II-й закон Кирхгофа в векторной форме при одном токе I имеет вид u_r1+u_r2+u_C = u, в соответствии с которым построена векторная диаграмма цепи (рис. 3.4,б).

Из прямоугольного треугольника напряжений (наружный треугольник)

u = = = 352 B,

 = arctg = arctg = -53.

Мгновенное значение напряжения сети

u(t)= U_msin(ωt+ψ_i+) = u sin(ωt+15+(-53)) = 352 sin(ωt – 38) B.

Напряжение на конденсаторе по фазе отстаёт от тока на 90, его мгновенное значение u_C(t)= 398,1sin(ωt – 75) B.

Напряжение на участке r₂-C, приложенное к ваттметру и вольтметру, рассчитаем по треугольнику напряжений u₂-u_r2-u_C:

u₂ = u_W = = = 315 B.

Вольтметр схемы рис. 3.4,а измеряет действующее значение напряже-ния u₂ = 315 B.

Показание ваттметра: P_W = u_W I_W cos .

В нашем примере I_W = I, поэтому

P_W = u₂Icos ₂ = I(u₂cos ₂)= Iu_r2= IIr₂ = I ²r₂ = P₂ – активная мощность, потребляемая сопротивлением r₂, и P₂ = 7,07²20 = 1000 Bт.

З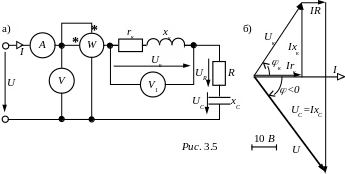 АДАЧА 3.4. Найти токи и напряжения в электрической цепи рис. 3.5,а, если: активное сопротивление катушки r_к = 4 Ом, индуктивное сопротивле-ние катушки х_к = 6 Ом, активное сопротивление реостата R = 2 Ом, ёмкост-ное сопротивление конденсатора х_С = 14 Ом, напряжение сети переменного тока U = 50 В. Построить векторную диаграмму цепи.

Решение

Ток цепи I, измеряемый амперметром А:

I = = = = 5 А.

Угол сдвига фаз цепи _вх = arctg = arctg = -53,13 < 0.

Вольтметр V измеряет входное напряжение U = 50 В.

Напряжение на катушке измеряется вольтметром V₁:

U_к = = I×Z_к = I× = 5× = 36 В.

Напряжение на реостате: U_R = I×R = 5×2 = 10 В,

напряжение на конденсаторе U_C = I×х_С = 5×14 = 70 В.

Векторная диаграмма цепи построена на рис. 3.5,б.

Ваттметр измеряет активную мощность цепи

Р = U×I×cos_вх = I ²×(r_к + R) = 5²×(4 + 2) = 150 Вт.

Обращаем внимание на то, что в последовательной цепи при наличии разнородных реактивных элементов (индуктивного и ёмкостного), напряже-ние на реактивном элементе может быть больше напряжения сети:

U_C = 70 В > U = 50 В.

ЗАДАЧА 3.5. В условиях задачи 3.4 при неизменном напряжении сети и параметрах r_к, х_к, R в широких пределах изменяется сопротивление кон-денсатора х_С(0).

Построить резонансные кривые I(х_С), U_L(х_С), U_С(х_С).

Решение

Ток в последовательной цепи рис. 3.5,а:

I = = А,

напряжение на индуктивности U_L = I×х_L = I×6 В,

напряжение на ёмкости

U_С = I×х_С =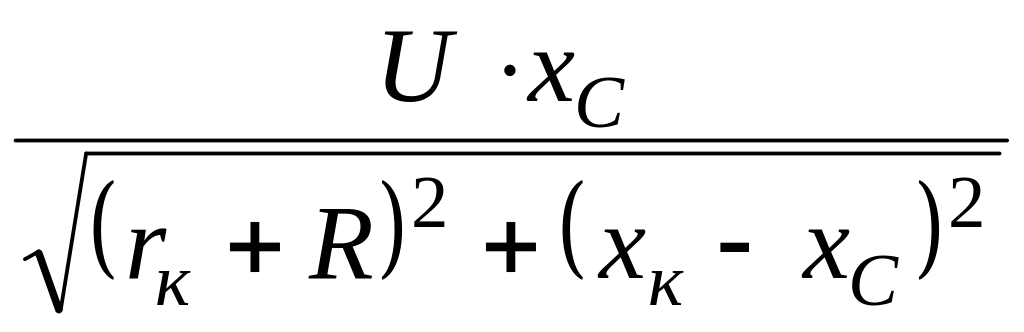 = 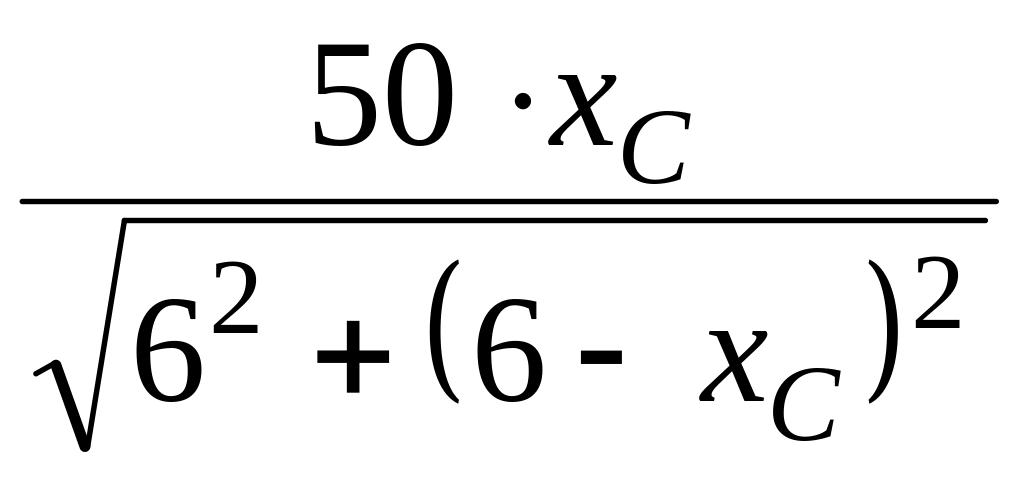В.

Результаты расчёта резонансных кривых сведены в табл. 3.3.

Таблица 3.3

хС, Ом	0	2	4	6	8	10	12	14	20	30	
I, А	5,89	6,93	7,9	8,33	7,9	6,93	5,89	5	3,28	2,02	0
UL, В	35,4	41,6	47,4	50	47,4	41,6	35,4	30	19,7	12,1	0
UС, В	0	13,9	31,6	50	63,2	69,3	70,7	70	65,6	60,6	U = 50

В табл. 3.3 выделена колонка, когда х_к=х_С=6 Ом и в цепи наступает резонанс напряжений U_L=U_С. При этом входное сопротивление цепи минимальное Z_{вх min} = r_к+R = 6 Ом,

а ток максимальный I_max = = = 8,33 A.

Кривая напряжения U_L повторяет по форме кривую тока, так как х_к=const, и тогда U_Lmax = I_max×х_к = 8,33×6 = 50 В.

Найдём максимальное значение U_Сmax в зависимости от х_С, исследовав кривую U_С(х_С) на максимум.

Координата х_С при U_С = U_Сmax определится уравнением

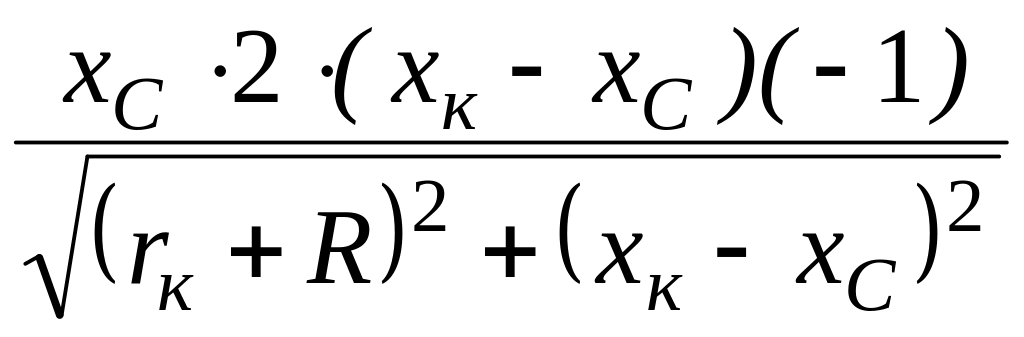= 0 или – = 0,

(r_к+R)² + х_к² – 2 х_к х_С + х_C² + х_к х_С – х_C² = 0,

откуда = =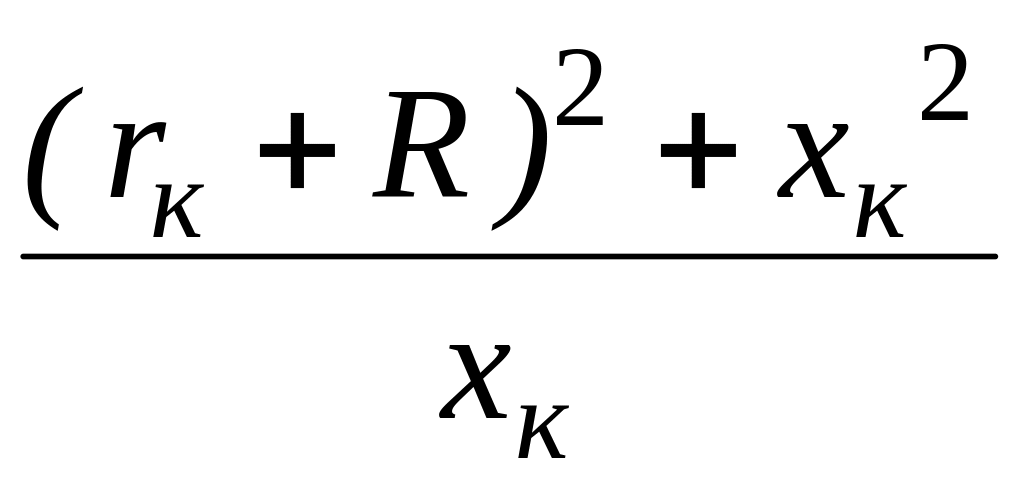 = 12 Ом.

Р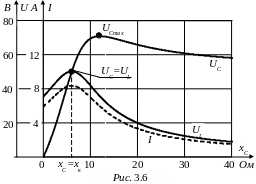 езонансные кривые приведены на рис. 3.6.

ЗАДАЧА 3.6. Определить показания приборов в схеме рис. 3.7,а, мгновенное значение тока i₁ в неразветвлённой части схемы, построить векторную диаграмму, если:

u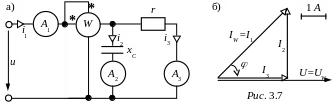 (t)= 200sin(ωt+25) В, r = 50 Ом, х_С = 50 Ом.