4. Інтеграл і його застосування
Варіант 5
Завдання 1 – 6 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну , на вашу думку , відповідь.
1. Знайдіть дві первісні для функції f (x) = 4 x3.
А |
Б |
В |
Г |
Д |
4х4 + 1 4х4 – 2 |
х4 + 1 х4 – 3 |
х4 + 3 х4 – 3x |
|
12х2 + 1 12х2 + 4 |
2. Знайдіть загальний вигляд первісної для функції f (x) = 8х
А |
Б |
В |
Г |
Д |
2х4 + С |
8х2 + С |
4х2 + С |
4х2 + х |
4х + С |
3. Для функції f знайдіть первісну F, якщо f(x) = 2х4, F(1) = 1.
А |
Б |
В |
Г |
Д |
0,2х5 + 0,8 |
2х5 - 1 |
0,5х5 + 0,5 |
х5 + 1 |
0,4х5 + 0,6 |
4. Обчисліть
інтеграл
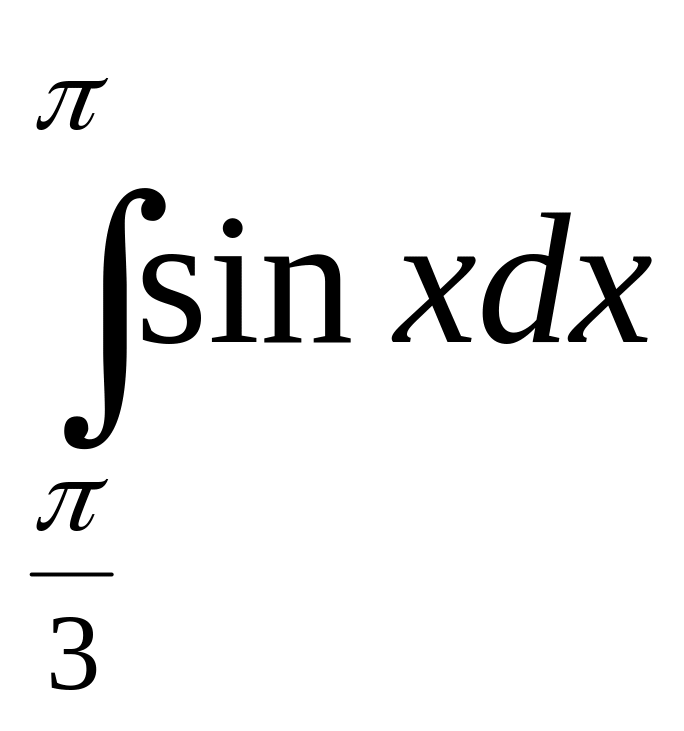
А |
Б |
В |
Г |
Д |
-1,5 |
|
|
1,5 |
-1,5 |
5.
Обчисліть інтеграл
А |
Б |
В |
Г |
Д |
14 |
9 |
15,5 |
16,5 |
11 |
6.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Розв’яжіть завдання 7. Відповідь запишіть десятковим дробом.
7. Знайдіть площу фігури, обмеженої лініями у = (х + 2)2 ; у = 0; х = 3 .
4. Інтеграл і його застосування
Варіант 6
Завдання 1 – 6 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну , на вашу думку , відповідь.
1. Знайдіть дві первісні для функції f (x) = 4 x3.
А |
Б |
В |
Г |
Д |
6х - х 6х –х + 1 |
х3 - 2 х3 + 4 |
х3 – х2 + 1 х3 – х2 + 4 |
х3 – х + 1 х3 – х + 3 |
3х3 – х 3х3 – х + 1 |
2. Знайдіть загальний вигляд первісної для функції f (x) = 12х
А |
Б |
В |
Г |
Д |
4х3 + С |
3х4 + С |
12 + С |
6х2 + С |
12х2 + С |
3. Для функції f знайдіть первісну F, якщо f(x) = 2х3, F(2) = 5.
А |
Б |
В |
Г |
Д |
х4 + 3 |
х4 - 11 |
|
|
6х + 7 |
4. Обчисліть
інтеграл
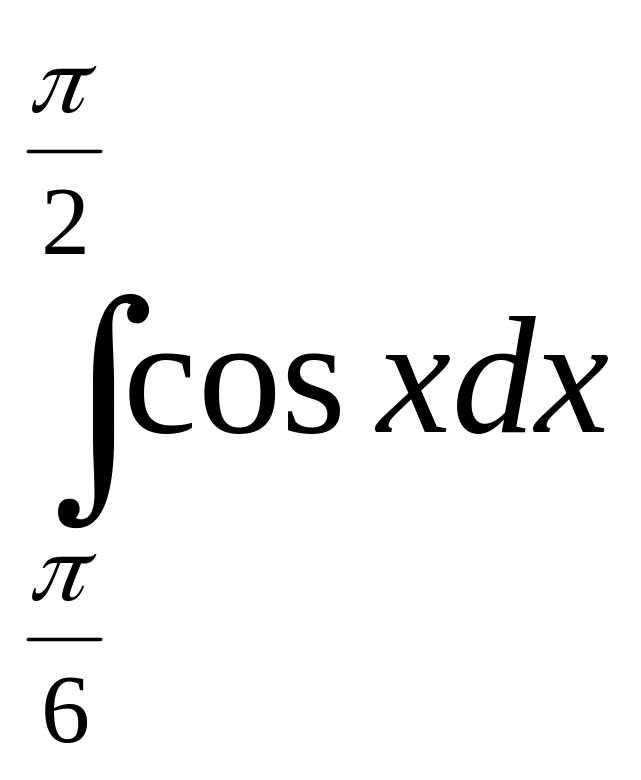
А |
Б |
В |
Г |
Д |
1,5 |
-1,5 |
0,5 |
-0,5 |
0 |
5.
Обчисліть інтеграл
А |
Б |
В |
Г |
Д |
32 |
30 |
24 |
28 |
25 |
6.
А |
Б |
В |
Г |
Д |
|
|
|
|
|
Розв’яжіть завдання 7. Відповідь запишіть десятковим дробом.
7. Знайдіть площу фігури, обмеженої лініями у = х2 + 3 ; у = 0; х = -1; х = 2 .