Исходные данные.
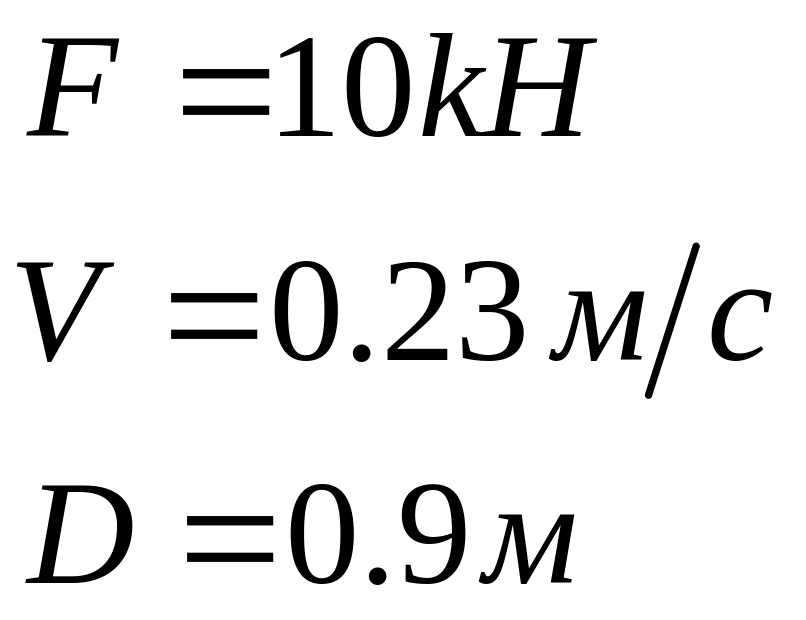
Где F- тяговое усилие в цепи конвейера; V- скорость движения цепи;
D- диаметр звездочки цепи конвейера.
Двигатель
Муфта с упругим элементом
Корпус
Муфта кулачково-дисковая
Вал
Подшипник
Редуктор цилиндрический 2-х ступенчатый
U1=24
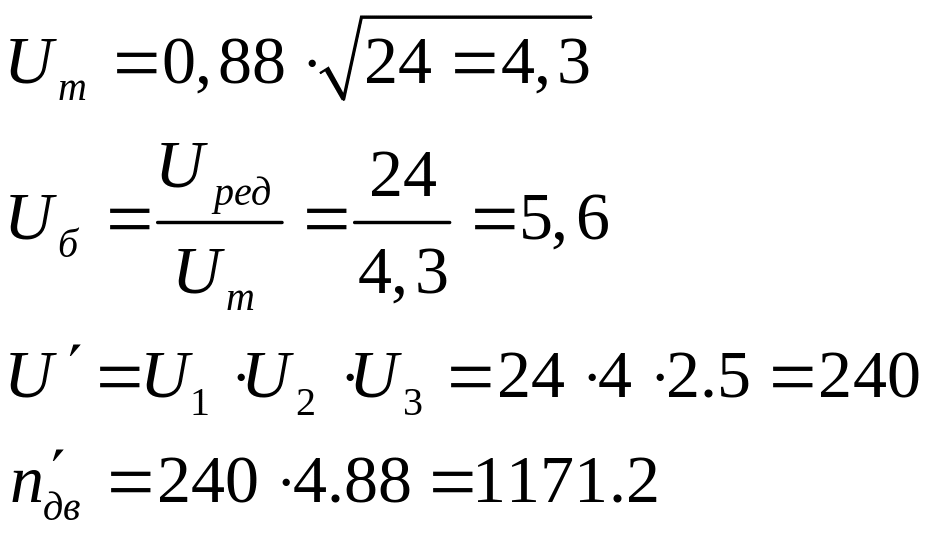
Определяем КПД привода
Цилиндрическая
передача закрытая
Коническая передача
открытая
Муфта с упругим элементом
Муфта кулачково-дисковая
Подшипники качения
Цилиндрическая
передача открытая
Подшипники скольжения
Определим потребительную мощность двигателя
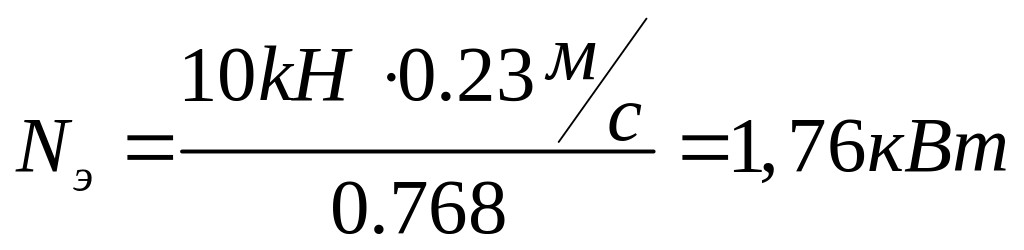
Выбираем по ГОСТ
;
;
тип двигателя: 4А90L4
Определяем действительное передаточное отношение
Определим частоту вращения всех валов привода
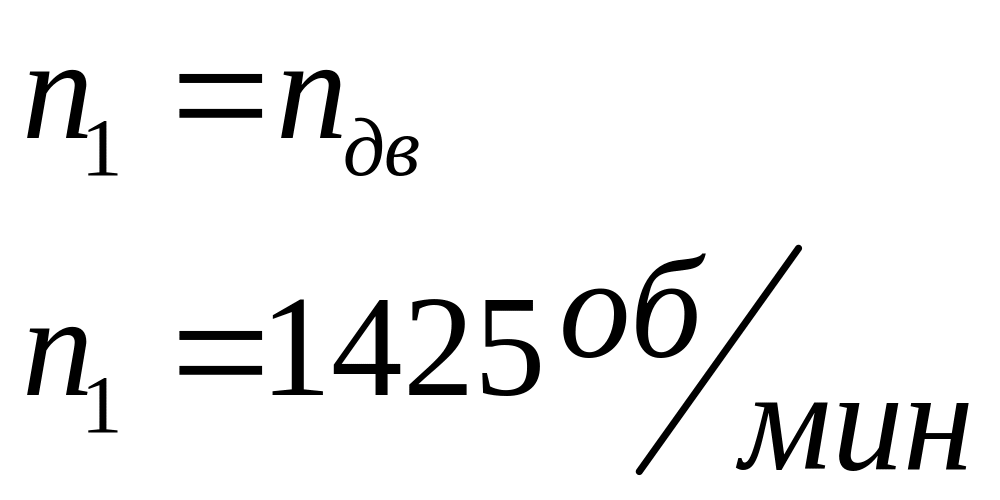
Определим мощности передаваемые валами:
Определяем крутящие моменты на каждом валу привода
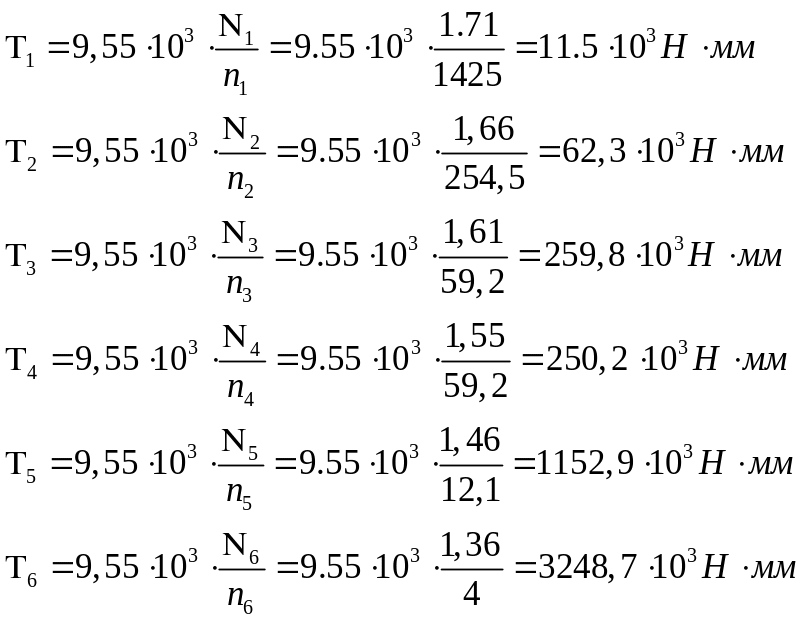
Расчёт зубчатой конической передачи.
Для шестерни
сталь 45
Термическая обработка: нормализация
Твердость: НВ215
Для колеса
сталь 45
Термическая обработка: нормализация
Твердость: НВ 200
Проектировочный расчёт.
Проектировочный расчёт закрытых передач (передач редукторов) проводится по условию контактной выносливости активных поверхностей зубьев для предотвращения их усталостного выкрашивания.
Межосевое расстояние
,
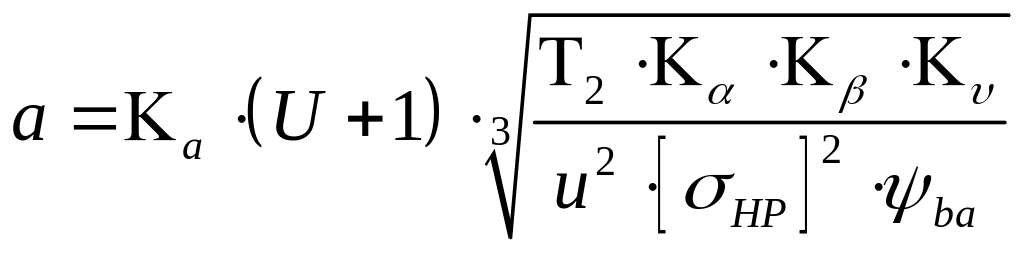где
- внешнее конусное расстояние, мм
U– передаточное число,
- крутящий момент
на колесе,
,
- допускаемое
контактное напряжение, МПа,
- коэффициент,
учитывающий распределение нагрузки
между зубьями,
- коэффициент,
учитывающий распределение нагрузки по
ширине венца,
- коэффициент,
учитывающий динамическую нагрузку,
возникающую в зацеплении,
- вспомогательный
коэффициент.
Вспомогательный коэффициент :
Для косозубых
цилиндрических передач при
,
Коэффициент
:
Для косозубых передач =1,1
Вспомогательный
параметр
:
Отражает зависимость рабочей ширины зацепления относительно среднего диаметра шестерни
определяется по таблице для консольного расположения шестерни относительно опор =0,8;
Коэффициент
:
Ориентировочные
значения коэффициента определяются по
таблице по параметру
для консольного расположения шестерни
относительно опор. В нашем случае при
и
=0,8
коэффициент
.
Коэффициент
:
При
примем
.
Допускаемое контактное напряжение:
Допускаемое
напряжение определяется , обычно, для
материала колеса, так как
.
,
где
- предел контактной
выносливости, соответствует эквивалентному
числу циклов перемен напряжений, МПа,
- коэффициент
безопасности,
- коэффициент,
учитывающий шероховатость рабочих
поверхностей зубьев,
-
коэффициент, учитывающий влияние
окружной скорости.
- коэффициент
долговечности (определяется из
гистограммы),
,
,
,
Принимаем min допустимое контактное напряжение
Проверочный расчёт на контактную прочность.
Расчёт проводится при действии максимальной (пусковой) нагрузки для предотвращения остаточной деформации или хрупкого разрушения поверхностного слоя зубчатых колёс.
Условие прочности:
,
где
- контактное
напряжение при действии максимальной
нагрузки, МПа.
- допускаемое
напряжение при действии максимальной
нагрузки, МПа.
- предел текучести,
МПа.
,
- условие выполняется.
Геометрические параметры колёс.
Число зубьев шестерни и колеса:
Из условия
неподрезания зубьев
.
Для закрытых
передач рекомендуется число зубьев
шестерни выбирать
,
для скоростных передач и тихоходных -
.
В нашем случае,
число зубьев шестерен:
.
Число зубьев
колеса:
.
Модуль передачи
;
.
Межосевое расстояние
мм;
мм.
Рабочая ширина зацепления
Проверим зубья
для предотвращения усталостного излома.
Определяем коэффициент формы зуба
в зависимости от
.
Для косозубой передачи
находим по эквивалентному числу:
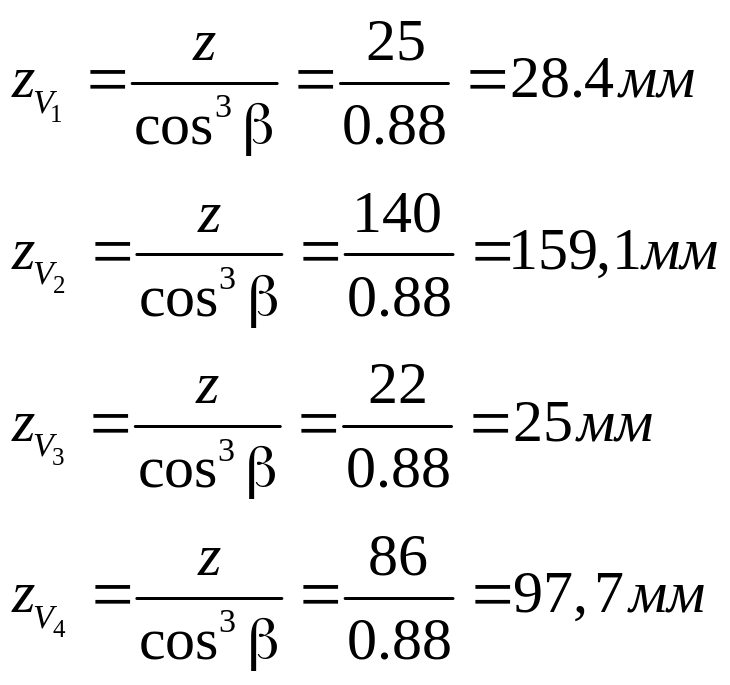
Коэффициент, учитывающий форму зуба:
.
Определяем наиболее слабый элемент конструкции по минимальному соотношению:
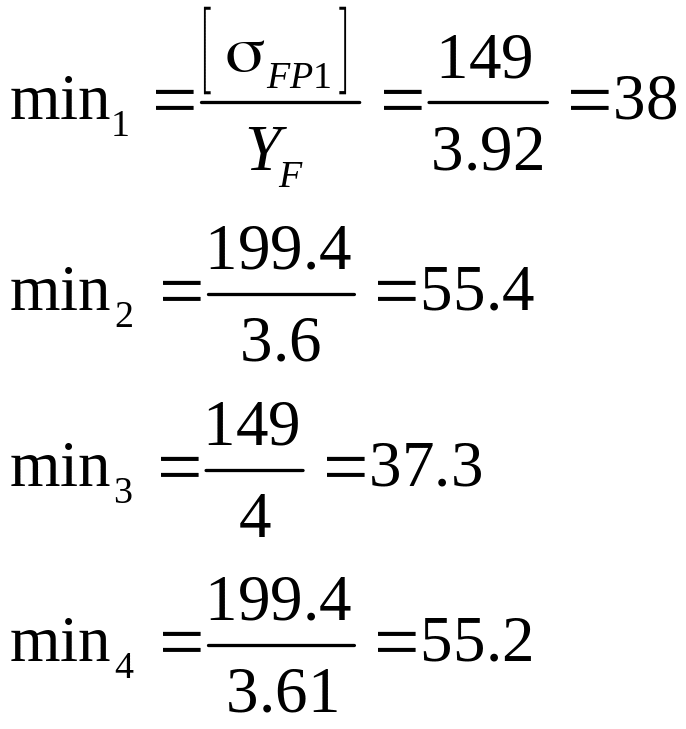
Наиболее слабым элементом передачи является шестерня на валу №2 редуктора.
Для наиболее слабого элемента определяем напряжения изгиба, действующие в ножке зуба:
Проведем проверочный расчет для предотвращения остаточной деформации или хрупкого излома зубьев при действии максимальной нагрузки. Определим максимальное допускаемое напряжение изгибу:
Определяем наиболее слабый элемент передачи:
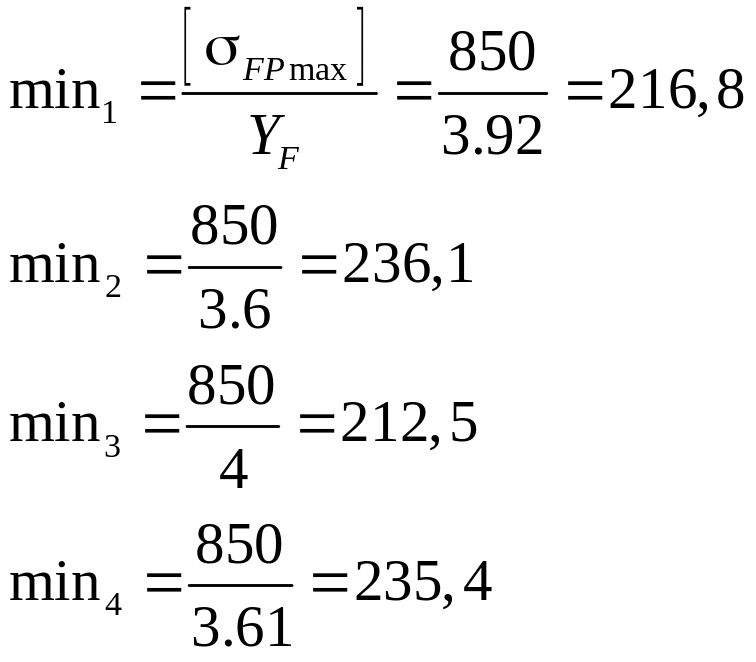
Максимальное
напряжение изгибу при действии
максимальной нагрузки
:
Проведем сравнение:
- условие выполняется.