2.5. Метод коллокаций
В методе коллокаций неизвестные параметры находятся из условия равенства нулю невязки в точках коллокации. Внесем аппроксимирующую функцию (2.2.2) в дифференциальное уравнение (2.1.1)
(2.5.1)
и
потребуем, чтобы невязка
была равна нулю в двух точках коллокации
при x1=l/2
и x2=l
( очевидно, что при этом число удерживаемых
членов ряда должно быть равно числу
точек коллокации):
(2.5.2)
или после подстановки значений синусов
(2.5.3)
Решим систему способом Крамера.
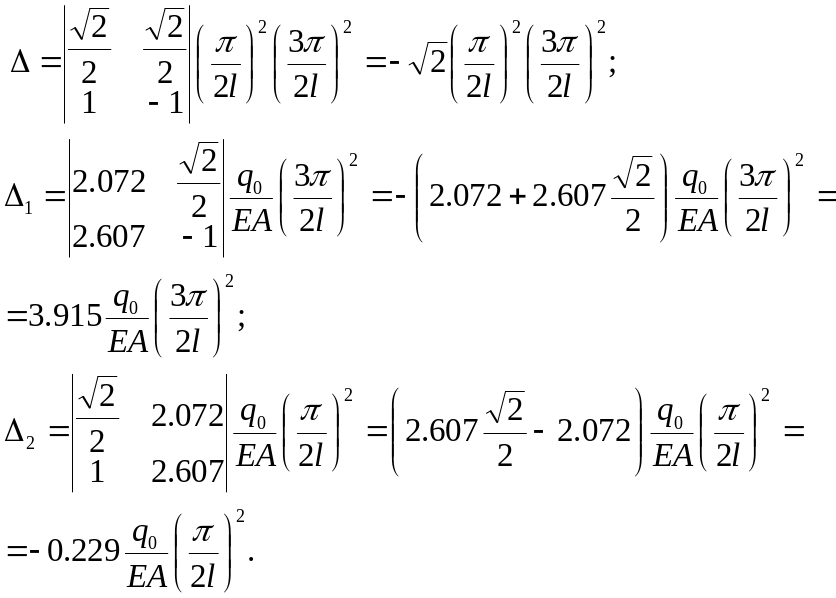(2.5.4)
Найдем численные значения неизвестных параметров, приводя к размерности точного решения:
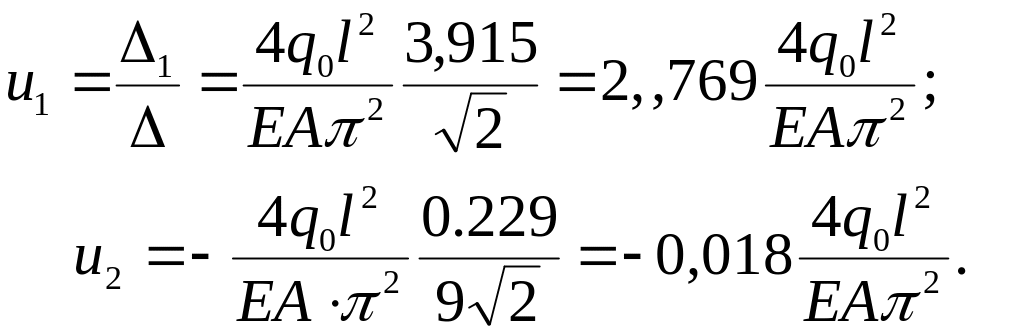(2.5.5)
Выражение для продольного перемещения примет вид:
(2.5.6)
Дифференцируя и умножая на жесткость растяжения-сжатия ЕА, приходим к выражению для продольного усилия:
(2.5.7)
Результаты счета при двух точках коллокации представлены в таблице 4 и рис. 10, 11.
Таблица 4
|
0 |
0,25 |
0,5 |
0,75 |
1,0 |
|
0 (0) |
1,047 (1,174) |
1,945 (2,040) |
2,552 (2,594) |
2,787 (2,787) |
|
2,715 (3,377) |
2,538 (2,606) |
1,996 (1,819) |
1,013 (0,963) |
0 (0) |
Рис. 10. Изменение продольного перемещения по длине стержня (метод коллокаций).
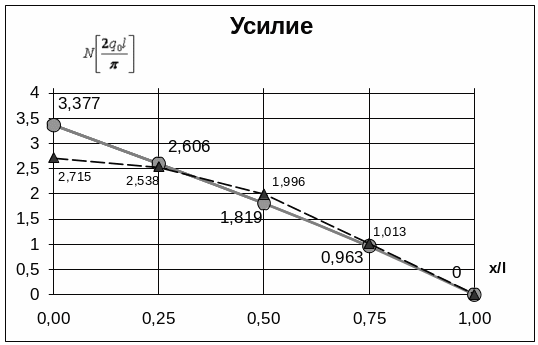
Рис. 11. Изменение нормального усилия по длине стержня (метод коллокаций).
2.6. Метод конечных элементов
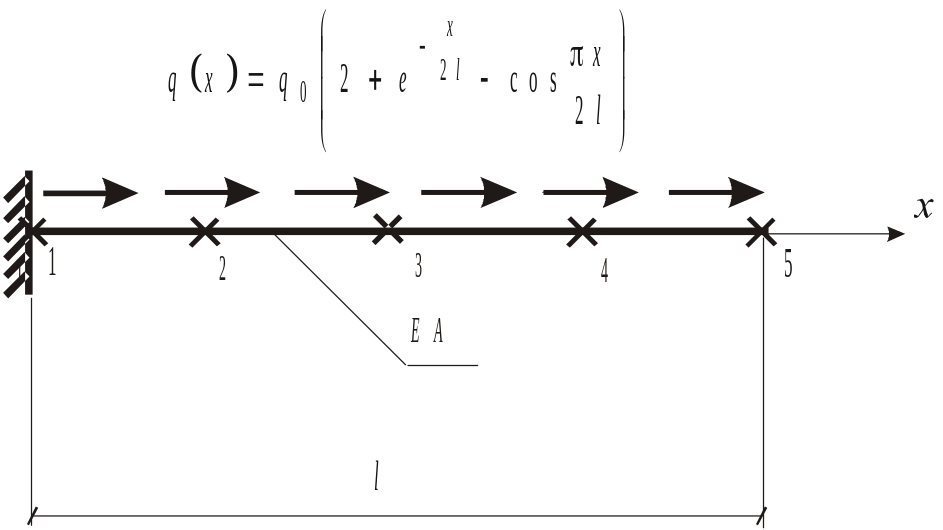
Рис. 12. Разбиение стержня на элементы
Для отдельного конечного элемента матрица жесткости имеет вид:
,
(2.6.1)
матрица преобразования нагрузки (грузовая матрица)-
,
(2.6.2)
вектор внешних нагрузок:
.
(2.2.3)
Матричное уравнение метода перемещений в конечноэлементной форме
.
(2.6.4)
Здесь: матрица жесткости всей системы – [K], формирующаяся в соответствии с топологией системы; вектор неизвестных узловых перемещений – {U}; грузовой вектор системы -
,
(2.6.5)
содержащий грузовую матрицу системы – [B] и вектор внешних нагрузок системы – {Q}.
Учитывая число участков (конечных элементов), запишем (2.6.4) для нашего примера в раскрытом виде:
.
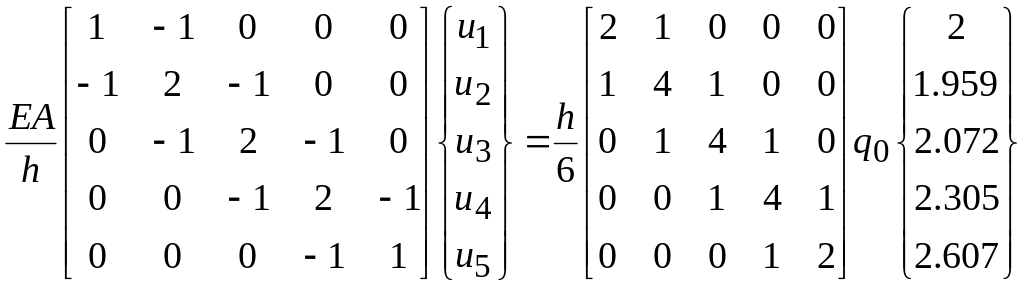(2.6.6)
Умножая матрицу преобразования на вектор узловых значений нагрузки, перепишем (2.2.6) в виде:
.
(2.6.7)
Геометрическое граничное условие (u1=0) учтем, обнуляя строку и столбец с общим диагональным элементом – множителем при u1 (сам диагональный элемент при этом не обнуляется) и соответствующие элементы грузового вектора. Система (2.6.7) приобретет окончательный вид:
.
(2.6.8)
Выполним прямой ход снизу:
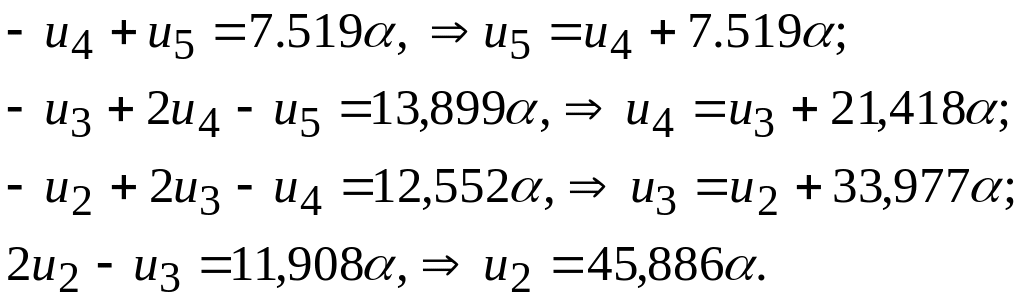(2.6.9)
Выполним обратный ход, приводя к размерности точного решения
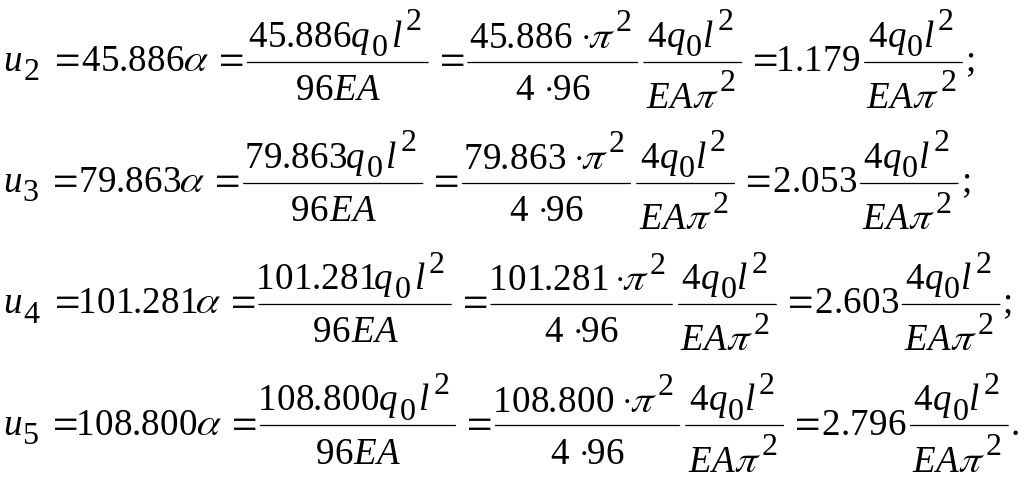(2.6.10)
Осуществим переход к нормальным усилиям с помощью соотношения:
.
(2.6.11)
Первый элемент:
.
(2.6.12)
Второй элемент:
.
(2.6.13)
Третий элемент:
.
(2.6.14)
Четвертый элемент:
.
(2.6.15)
Воспользуемся дифференцирующей матрицей
.
(2.6.16)
Результаты расчета представим в виде таблицы 3 и графиков (рис. 8,9).
Таблица 5
|
0 |
0,25 |
0,5 |
0,75 |
1,0 |
|
0 (0) |
1,179 (1,174) |
2,053 (2,040) |
2,603 (2,594) |
2,796 (2,787) |
|
3,002 3,392 (3,377) |
2,223 2,613 (2,606) |
1,403 1,813 (1,819) |
0,491 0,947 (0,963) |
- 0,036 (0) |
(…) – точное решение; * - решение в рамках МКЭ; ** - решение с помощью дифференцирующей матрицы.
Рис. 13. Изменение перемещения по длине стержня (метод конечных элементов)
Рис. 14. Изменение продольного усилия по длине стержня (метод конечных элементов)
PROGRAM GAUSS1;
{Решение систем уравнений методом Гаусса }
uses crt;
const
n=5;
A: array [1..n,1..n] of real=((2,-1,0,0),(0,-1,2,-1,0),(0,0-1,2,-1),(0,0,0,-1,2),(0,0,0,-1,1));
B: array [1..n] of real=(11.908,12.552,13.899,7,519,0);
var
i,j,k: integer;
H: real;
X: array [1..n] of real;
BEGIN
clrscr;
for i:=1 to n-1 do begin
for j:=i+1 to n do begin
A[j,i]:=-A[j,i]/A[i,i];
for k:=i+1 to n do begin
A[j,k]:=A[j,k]+A[j,i]*A[i,k];
end;
B[j]:=B[j]+A[j,i]*B[i];
end;
end;
X[n]:=B[n]/A[n,n];
for i:=n-1 downto 1 do begin
H:=B[i];
for j:=i+1 to n do begin
H:=H-X[j]*A[i,j];
end;
X[i]:=H/A[i,i];
end;
writeln;
writeln(' Номер точки Перемещение ');
for i:=1 to n do begin
writeln;
writeln(' i=',i,' X[i]=', X[i]:7:4);
end;
readln;
END.