
- •Вариант 00-в
- •1. Точное решение
- •2.1. Приближенное решение (метод конечных разностей)
- •2.2. Метод Бубнова-Галеркина
- •Дифференциальное уравнение упругого равновесия растяжения-сжатия стержня имеет вид:
- •Запишем аппроксимирующую функцию
- •2.3. Метод Ритца-Тимошенко
- •2.4. Метод наименьших квадратов
- •2.5. Метод коллокаций
- •2.6. Метод конечных элементов
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
Вятский Государственный Университет
Инженерно-строительный факультет
Кафедра строительных конструкций
ЗАЧЕТНАЯ РАБОТА
По курсу «Математическое моделирование в строительстве»
(Вариант В – образец)
Выполнил ст-т гр. С-
___________________
Принял преподаватель
___________________ Буравлев В.Ф.
Киров 2010
Вариант 00-в

Рис. 1. Расчетная схема
1. Точное решение
Дифференциальное уравнение равновесия имеет вид:
![]() (1.1)
(1.1)
Дважды интегрируем
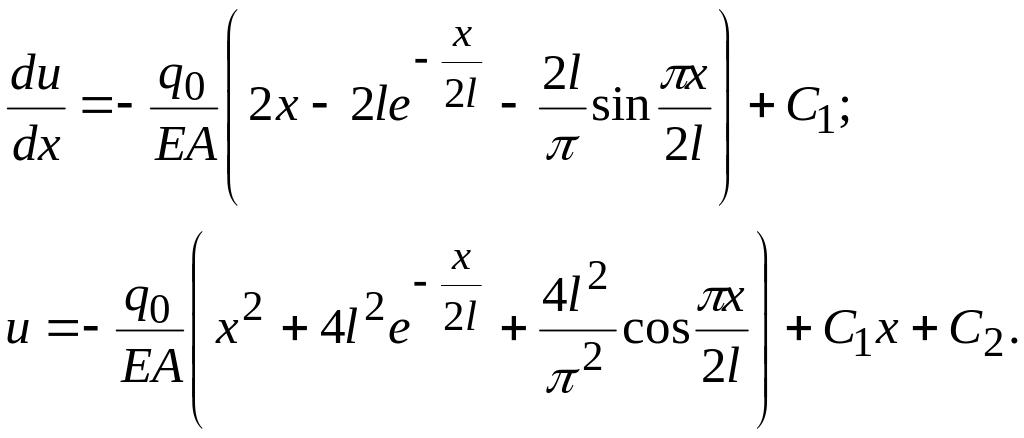 (1.2)
(1.2)
Удовлетворяем геометрическому граничному условию на левом торце
![]()
откуда
![]() .
(1.3)
.
(1.3)
Удовлетворяем статические граничные условия на правом торце
![]()
откуда
![]() (1.4)
(1.4)
Внося полученные константы интегрирования (1.3) и (1.4) во второе соотношение (1.2), приходим к выражению для продольного перемещения
 (1.5)
(1.5)
Умножая на EА и беря производную по x, получим выражение для нормального усилия
 (1.6)
(1.6)
Произведем расчет перемещений и усилий по формулам (1.5( и (1.6) c помощью программы на языке программирования «Pascal» в пяти равноотстоящих точках и сведем результаты расчета в таблицу 1.
PROGRAM STTRB;
uses crt;
const
qo=1.0; l=1.0; EA=1.0; m=4;
var i: integer;
qoln,qolu,dx,x,x3: real;
u,N: array[1..m+1] of real;
BEGIN
clrscr;
qoln:=2*qo*l/pi;
qolu:=2*qoln*l/(pi*EA);
dx:=l/m;
p2:=pi/2;
pi2:=sqr(pi);
writeln;
writeln(' Результаты расчета');
writeln;
writeln('Номер точки Координата Перемещение Усилие');
for i:=1 to m+1 do
begin
x:=dx*(i-1)/l;
p2x:=p2*x;
ex:=exp(-x/2);
xp:=pi*(1-exp(-1/2)-1;
u[i]:={qolu*}(-sqr(p2x)-pi2*ex-cos(p2x)+p2*x*xp+1+pi2);
N[i]:=-{qoln*}(-pi*x+pi*ex+sin(p2x)+xp);
writeln;
writeln(' i=',i,' x=',x:5:3,' u=',u[i]:7:4,' N=',N[i]:7:4);
end;
readln;
END.
Представим результаты расчета в виде таблицы 1 и графиков (рис. 2 и 3)
Таблица 1
|
0 |
0,25 |
0,5 |
0,75 |
1,0 |
|
0 |
1,174 |
2,040 |
2,594 |
2,787 |
|
3,377 |
2,606 |
1,819 |
0,963 |
0 |
.

Рис. 2. Изменение перемещения по длине стержня (точное решение)

Рис. 3. Изменение продольного усилия по длине стержня (точное решение)
2.1. Приближенное решение (метод конечных разностей)
Обозначим узловые точки (1-5) в местах разбиения стержня на четыре элемента и введем законтурную точку 6 (рис. 4).

Рис. 4. Разбиение стержня на элементы
Запишем дифференциальное уравнение в конечно-разностной форме
 (2.1.1)
(2.1.1)
Здесь введено обозначение
![]() (2.1.2)
(2.1.2)
Запишем уравнение для всех внутренних точек, причем для крайней правой точки 5 запишем статическое граничное условие через законтурную точку 6:
 (2.1.3)
(2.1.3)
Выполним
прямой ход, учитывая левое геометрическое
граничное условие
![]() :
:
 (2.1.4)
(2.1.4)
Выполним
обратный ход, раскрывая
![]() и приводя результат к размерности
точного решения:
и приводя результат к размерности
точного решения:
 (2.1.5)
(2.1.5)
Осуществим переход к нормальным усилиям с учетом размерностей для перемещений и усилий в точном решении при помощи соотношения
![]() ,
(2.1.6)
,
(2.1.6)
где черта над u обозначает, что берутся только ее численные значения.
 (2.1.7)
(2.1.7)
Воспользуемся соотношением, осуществляющем переход к усилиям с помощью дифференцирующей матрицы
![]() ,
(2.1.8)
,
(2.1.8)
которое в раскрытом виде с учетом числа элементов (h=l/4) и размерностей, использованных для перемещений и усилий в точном решении, запишется так:
 .
(2.1.9)
.
(2.1.9)
Результаты расчета представим в виде таблицы 2 и графиков (рис. 5,6).
Таблица 2
|
0 |
0,25 |
0,5 |
0,75 |
1,0 |
|
0 (0) |
1,178 (1,174) |
2,054 (2,040) |
2,611 (2,594) |
2,812 (2,787) |
|
2,862 3,384 (3,377) |
2,146 2,615 (2,606) |
1,413 1,823 (1,819) |
0,514 0,975 (0,963) |
- 0,060 (0) |
(…) – точное решение; * - решение в рамках МКР; ** - решение с помощью дифференцирующей матрицы.

Рис.
5. Изменение перемещения по длине стержня
(метод конечных разностей)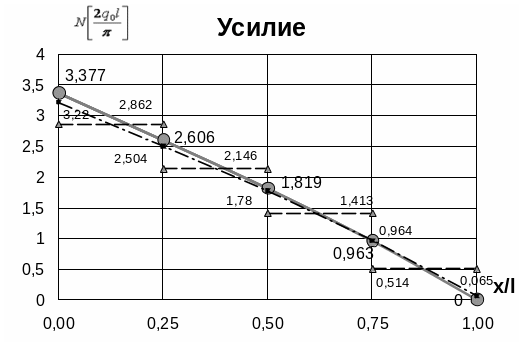 Рис. 6. Изменение продольного усилия по
длине стержня (метод конечных разностей)
Рис. 6. Изменение продольного усилия по
длине стержня (метод конечных разностей)
Текст программы для решения системы уравнений

