Тема 2.3. Основы математической статистики

Статистика, строгая муза, Ты реешь над каждой судьбой. Никто для тебя не обуза, Никто не обижен тобой.

В. Шефнер [13]

Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи. В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей – свойства и взаимосвязи этих величин (распределений).

Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.

При этом возникают, например, следующие вопросы: если мы наблюдаем одну случайную величину – как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении? Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин,– что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?

Часто бывает возможно высказать некие предположения о распределении, спрятанном в «черном ящике», или о его свойствах. В этом случае по опытным данным требуется подтвердить или опровергнуть эти предположения («гипотезы»). При этом надо помнить, что ответ «да» или «нет» может быть дан лишь с определенной степенью достоверности, и чем дольше мы можем продолжать эксперимент, тем точнее могут быть выводы. Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента. Примером такого эксперимента может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.

Предметом исследования в математической статистике является совокупность объектов, однородных относительно некоторых признаков.

Например, физическая подготовленность мальчиков 10 лет г. Уссурийска; пловцы – мастера спорта России.

Совокупность из всех объектов, объединенных этими признаками, называется генеральной (или общий ряд данных). Задачей исследования является изучение признаков генеральной совокупности, которые определяются влиянием некоторых случайных факторов. Например, изучение физической подготовленности мальчиков 10 лет г. Уссурийска.

Для решения задач исследования проводится эксперимент (измерение, тестирование, анкетирование), в результате которого получают значение некоторой случайной величины (результаты тестирования, количество баллов). Если в эксперименте участвуют все объекты генеральной совокупности, то такое обследование называют сплошным.

На практике обычно применяют выборочный метод, который заключается в том, что из генеральной совокупности случайным образом извлекают n элементов. Эти элементы называются выборочной совокупностью или выборкой. Количество элементов в выборке называется ее объемом. Исследователь изучает и анализирует выборочную совокупность и на основании полученных показателей делает вывод о параметрах генеральной совокупности.

Допустим, из генеральной совокупности извлечена выборка объемом n, измерена некоторая величина Х, в результате чего получен ряд значений х₁, х₂, . . . х_n. Этот ряд называется простым статистическим рядом.

Пример: измерена масса тела 10 девочек 6 лет. Полученные данные образуют простой статистический ряд:

24, 22, 23, 28, 24, 23, 25, 27, 25, 25.

Отдельные значения статистического ряда называются вариантами. Если варианта х_i появилась m раз, то число m называют частотой, а ее отношение к объему выборки m/n – относительной частотой.

Последовательность вариант, записанная в возрастающем (убывающем) порядке, называется ранжированным рядом.

Пример: ранжированный ряд:

22, 23, 23, 24, 24, 25, 25, 25, 27, 28.

Таблица, в первой строке которой записаны все значения величины (варианты), во второй – соответствующие им частоты, называется таблицей распределения.

Пример: таблицы распределения:

Х	22	23	24	25	27	28
m	1	2	2	3	1	1

Графическим изображением таблицы распределения является полигон.

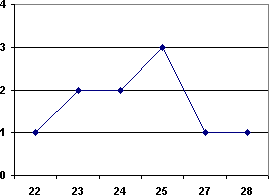
Для его построения на оси О_Х откладывают значения вариант, на оси О_У – соответствующие им частоты. Точки с координатами (х_i; m_i) соединяют отрезками, полученная ломаная линия называется полигоном частот.

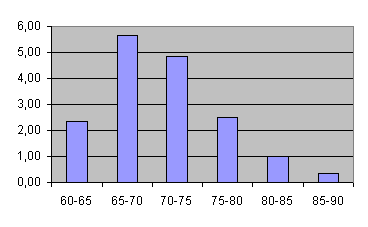
В том случае, если выборка представлена большим количеством различных значений непрерывной случайной величины, то группировку данных проводят в виде интервального вариационного ряда. Для этого диапазон варьирования признака разбивают на несколько (5-10) равных интервалов и указывают количество вариант, попавших в каждый интервал.

Графическим изображением интервального вариационного ряда является гистограмма. Для ее построения на оси О_Х откладывают интервалы шириной h, на каждом интервале строят прямоугольник высотой m/h. Величина m/h называется плотностью частоты. Гистограмма является эмпирическим аналогом графика дифференциальной функции распределения.

Есть несколько числовых характеристик выборки:

1. Размах выборки – это разница между минимальной и максимальной вариантой. На графике – это длина области определения полигона. На графике размах равен 28-22=6.

Размах

2. Мода выборки – это наиболее часто встречающаяся ее варианта. На графике – это наивысшая точка или наивысшие точки, так как мода может быть и не одна. На графике мода равна 25.

Мода

3. Среднее значение – это такое значение, которое усредняет все различные результаты, заменяя полную, но объемную информацию одним-единственным числом. Есть три способа его нахождения.

1. Сложить все результаты, входящие в выборку и полученную сумму разделить на количество всех результатов (стандартный способ). Например: (24+22+23+28+24+23+25+27+25+25):10=24,6.

2. Каждую варианту умножить на ее кратность, сложить все полученные результаты и поделить найденную сумму на сумму всех кратностей – объем выборки (самый популярный в статистике). Например: (22·1+23·2+24·2+25·3+27·1+28·1):10=24,6.

3. Каждую варианту умножить на ее частоту, затем сложить все полученные произведения (похоже на нахождение математического ожидания). Например: 22·0,1+23·0,2+24·0,2+25·0,3+27·0,1+28·0,1=24,6.

4. Дисперсия – оценивает степень разброса, отклонения от среднего значения, неоднородность группы. Есть два способа ее нахождения.

1. Из значения каждой варианты вычесть среднее значение, полученные разности возвести в квадрат и умножить на соответствующее значение кратности, затем сложить все полученные произведения и результат поделить на объем выборки. Например:

(22²·1+23²·2+24²·2+25²·3+27²·1+28²·1):10-24,6²=

=(484+1058+1152+1875+729+784):10-605,16=608,2-605,16=3,04

2. Квадрат значений каждой варианты умножить на ее кратность, сложить все полученные результаты и поделить найденную сумму на объем выборки, затем из получившегося числа вычесть квадрат среднего значения. Например:

(22²·0,1+23²·0,2+24²·0,2+25²·0,3+27²·0,1+28²·0,1)-24,6²=

=(48,4+105,8+115,2+187,5+72,9+78,4)-605,16=608,2-605,16=3,04

5. Среднее квадратичное отклонение – также оценивает степень разброса, отклонение от среднего значения и равно корню квадратному из дисперсии. Например: 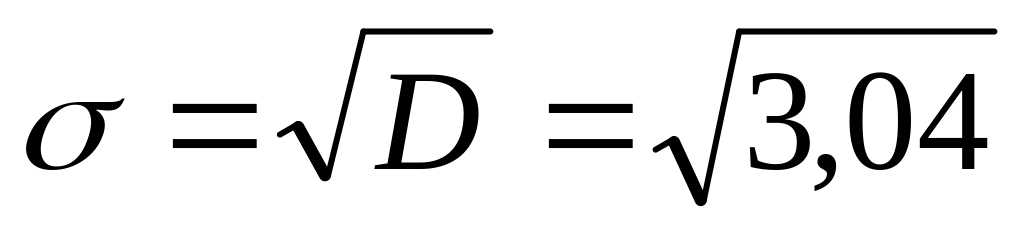=1,74. [1]

Задачи

94. Абитуриенты на четырех вступительных экзаменах набрали в сумме такие количества баллов: 17, 12, 19, 16, 18, 17, 13, 13, 19, 20, 18, 13, 12, 20, 20, 13, 17, 17, 16, 19. Составьте ранжированный ряд данных.

95. Составьте таблицу распределения для выборки из задания 1.

96. Выписали месяцы рождения группы 2сб. Получился такой ряд: 3, 12, 11, 7, 10, 7, 11, 5, 12, 3, 3, 3, 12, 11, 10, 10, 7, 7, 12, 11. Составьте таблицу распределения.

97. Изобразите по данным из задания 1 полигон. Укажите моду и размах.

98. Изобразите по данным из задания 2 гистограмму.

99. В колледже культуры провели опрос: «Какой шоколадный батончик вы больше любите?» Ответы были следующие: 10 человек ответили «Пикник», 8 человек – «Твикс», 12 человек – «Сникерс», 5 человек «Марс», 9 человек «Баунти», 3 человек – «Милки Вей», 1 человек – «Несквик». Изобразите данные опроса графически.

100. Класс написал контрольную работу со следующими результатами: две двойки, четыре тройки, восемь четверок и шесть пятерок. Найти средний балл, разброс класса в оценках и сделать вывод о том, как в среднем класс справился с работой?

101. Для украшения зала к празднику «День знаний» организаторы купили шарики по разной цене: по 2 рубля 30 шариков, по 3 рубля – 30, по 4 рубля – 20, по 5 рублей – 20. Найдите среднюю цену за один шарик и разброс в цене. Изобразите данные с помощью полигона, укажите размах и моду.

102. В группе у двух человек по 9 грамот, у трех человек по 8 грамот, у четырех человек по 5 грамот и у одного человека 2 грамоты. Найти среднее количество грамот на группу, и неоднородность распределения в группе наград.

103. Оценки по дисциплине «Народный танец» за 2 семестр в группе хореографов таковы: четыре пятерки, шесть четверок, семь троек. Сделайте вывод о среднем балле и неоднородности группы.

104. В одном из магазинов перед праздником День студента была акция для студентов: возьми мороженного столько, сколько захочешь! Один из представителей торговой марки наблюдал за покупателями: сколько же штук мороженного возьмет каждый из участников акции. Результаты были такими: 1 мороженное взяли 20 человек, 2 мороженных – 30 человек, 3 мороженных – 20 человек, 4 мороженных – 15 человек, 5 мороженных 10 человек, 6 мороженных – 5 человек. Сколько мороженных в среднем взял каждый из студентов и каков разброс в их количестве?

105. Один класс написал контрольную работу со следующими результатами: две двойки, четыре тройки, восемь четверок и шесть пятерок. Другой класс написал эту же контрольную работу с такими результатами: шесть двоек, три тройки, четыре четверки, семь пятерок. Какой из классов в среднем лучше справился с работой, в каком ученики однороднее?

106. Сравните результаты итоговой аттестации двух групп:

1 группа	2	3	4	5	2 группа	2	3	4	5
	2	3	4	1		2	3	3	2

Сделайте вывод по каждой группе, изобразите сравнительные данные аттестации с помощью гистограммы.

94. На мероприятии «День здоровья» каждый из участников команды делал по одному выстрелу по мишени. Р

Результаты таковы:

Группа 1ХФ

Количество очков	10	9	8	7	6	5	4	3	2	1
Количество человек	1	5	2	2	3	4	2	0	0	1

Группа 1СБ

Количество очков	10	9	8	7	6	5	4	3	2	1
Количество человек	3	4	3	1	0	0	1	1	1	6

Какая из групп показала в среднем лучше результат, а какая из групп оказалась однороднее? Покажите данные на полигоне, для каждой группы указав моду и размах.