14) Парабола. Каноническое уравнение.

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директри­сой (см. рис. 60). В выбранной системе фокус F имеет координаты  , а уравнение директрисы имеет вид   , или  .

Пусть   — произвольная точка параболы. Соединим точку Μ с F. Проведем отрезок ΜΝ пер­пендикулярно директрисе. Согласно определению параболы MF = ΜΝ. По формуле расстояния между двумя точками на­ходим:

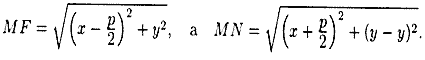
Следовательно,

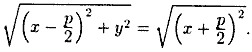
Возведя обе части уравнения в квадрат, получим

т. е.

 

15) Директриса эллипса и гиперболы

Директрисами гиперболы называются две прямые,уравнения которых в канонической для гиперболы системе координатимеют вид

                                       .

Так как  , то  .

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .

            Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

16) Полярное уравнение кривой второго порядка.

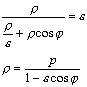             (3)

 Уравнение (3) называется уравнением кривой второго порядка в полярных координатах. При  >1 кривая является эллипсом, при  >1 - ветвью гипиерболы, при  =1 - параболой.

17) Преобразования дпск

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).

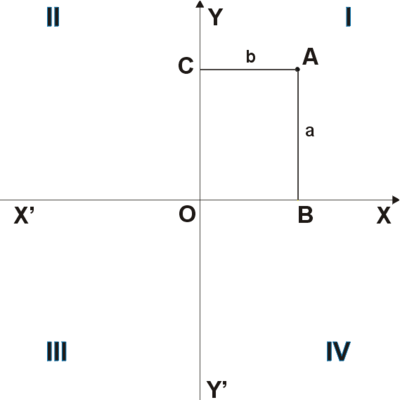
Рис. 1

Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

18) Упрощение обшего уравнения второй степени

Общее уравнение линии второго порядка имеет вид

Ax² + 2Bxy + Cy² + Dx + Ey + F = 0.

Задача упрощения этого уравнения состоит в том, чтобы в преобразованном уравнении были устранены: 1) член, содержащий произведение текущих координат, и 2) члены, содержащие первые степени двух координат или, по крайней мере, одной из них.

В том случае, когда уравнение линии второго порядка содержит произведение текущих координат, упрощение его следует начинать с поворота осей без изменения начала координат и надлежащим выбором угла поворота добиться того, чтобы из преобразованного уравнения был устранен член, содержащий произведение текущих координат. Преобразование координат в этом случае будем вести по формулам

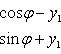
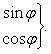
Если после устранения из преобразованного уравнения члена с произведением текущих координат в нем останутся члены с первыми степенями текущих координат, то последующим параллельным переносом осей можно, как это было показано, привести уравнение к каноническому виду.