1 Линейные операции над векторами. Пространство Rn

Суммой a + b двух векторов a и b называется вектор, идущий

из начала вектора a в конец вектора b при условии, что вектор b

приложен к концу вектора a. Правило сложения двух векторов, содержащееся в этом определении, называется правилом треугольника

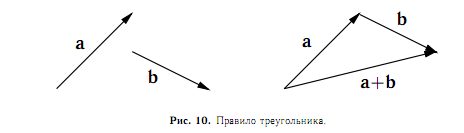
Сложение векторов коммутативно:  .

Сложение векторов ассоциативно:  .

1. a + b = b + a (переместительное свойство);

2. (a + b) + c= a + (b + c) (сочетательное свойство);

Из свойства 1. следует еще одно правило сложения векторов, называемое пра-

вилом параллелограмма: если векторы a и b приложены к общему началу и на

них построен параллелограмм, то сумма a +b (или b+a) этих векторов пред-

ставляет собой диагональ параллелограмма, идущую из общего начала векторов

a и b.

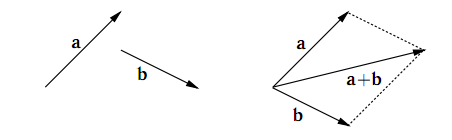
Свойства 1. - 2. позволяют распространить правило сложения на сумму

любого конечного числа векторов. При этом нет необходимости производить

сложение последовательно, фиксируя каждый промежуточный результат; сумма

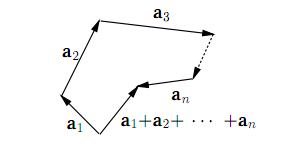
любого числа векторов может быть построена с помощью следующего правила:

если приложить вектор a2 к концу вектора a1, вектор a3 к концу вектора a2, · · ·

вектор an к концу вектора an−1, то сумма a1+a2+· · · +an будет представлять

собой вектор, идущий из начала вектора a1 в конец вектора an. Это правило

сложения, проиллюстрированное на рис. 12 называется правилом замыкания

ломаной до многоугольника

Разностью a - b вектора a и вектора b называется такой вектор

c, который в сумме с вектором b дает вектор a.

Непосредственно из определения и из правила треугольника сложения век-

торов вытекает следующее правило построения разности a - b: разность a - b

приведенных к общему началу векторов a и b представляет собой вектор,

идущий из конца вычитаемого вектора b в конец уменьшаемого вектора a.

Произведением αa (или aα) вектора a на вещественное число α

называется вектор b, коллинеарный вектору a, имеющий длину,

равную |α|·|a| , и имеющий направление, совпадающее с направле-

нием вектора a в случае α > 0 и противоположное направлению

вектора a в случае α < 0.

Операция умножения вектора на число обладает следующими свойствами:

1. α (a +b) = αa + αb (распределительное свойство числового сомно-

жителя относительно суммы векторов);

2. (α + β)a = αa+ βa (распределительное свойство векторного сомножи-

теля относительно суммы чисел);

3. α (β a)= (αβ)a (сочетательное свойство числовых сомножителей).

Определение. Пусть X — векторное пространство (над R). Скалярное произведение в

X — это функция, обладающая свойствами:

(1) Симметричность: (x; y) = (y; x) для любых x; y € X.

(2) Линейность по каждому аргументу (билинейность): (ax; y) = a(x; y), (x + y; z) =

(x; z) + (y; z) для любых x; y; z € X, a € R. Линейность по второму аргументу следует из

симметричности.

(3) Положительная определенность: (x; x) > 0 при всех x € X \ {0},

Евклидово пространство — это векторное пространство с заданным на нем скалярным

произведением.

2 Базис и координаты над векторы.

3 Скалярное произвеление

4 Векторное произведение

5 Смешанное произведение

6 Плоскость в пространстве

7) Нормированное уравнение плоскости

8) Прямая в пространстве

9) Системы координат

Система координат – опорная система для определения положения точек в пространстве или на плоскостях и поверхностях относительно выбранных осей, плоскостей или поверхностей.

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении осиY'Y вверх, ось X'X смотрела направо.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.