Т.А. Волкова, С.С. Соколов

Производная

(задания для выполнения расчетно-графических работ)

Федеральное агентство морского и речного транспорта

Федеральное бюджетнОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

высшего профессионального образования

Санкт-Петербургский государственный университет водных коммуникаций

Т.А. Волкова, С.С. Соколов

производная

(задания для выполнения расчетно-графических работ)

Рекомендовано Редакционно-издательским советом

Санкт-Петербургского государственного университета водных коммуникаций

Санкт-Петербург

2012

УДК 517.2

ББК 22.161

Рецензент:

Кандидат технических наук, доцент кафедры «Математика»

А.С. Кобелева

Т.А. Волкова, С.С. Соколов

ПРОИЗВОДНАЯ (ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ): учебно-методическое пособие – СПб.: СПГУВК, 2012 – 59с.

Учебно-методическое пособие содержит задания для выполнения расчетно-графических работ по курсу «Математика» и «Математический анализ» студентами, обучающимися на специальностях: 010501.65 «Прикладная математика и информатика», 090105.65 «Комплексное обеспечение информационной безопасности автоматизированных систем», 230201.65 "Информационные системы и технологии", - а также по направлениям бакалавриата: 010400.62 «Прикладная математика и информатика», 090900.62 «Информационная безопасность», 230400.62 "Информационные системы и технологии".

УДК 517.2

ББК 22.161

@Санкт-Петербургский государственный

университет водных коммуникаций, 2012

СОДЕРЖАНИЕ

Y

Задания 5

Производная 40

Основные свойства производной 40

Таблица производных 41

Производная параметрически заданной функции 44

Производная показательно-степенной функции 46

Вычисление приближенного значения функции с помощью дифференциала 47

Геометрический и механический смыслы производной 48

Геометрический смысл производной 48

Механический смысл производной 51

Исследование функций и построение графиков 52

Четность и нечетность функции 53

Условия монотонности функции 53

Экстремумы функции 54

Выпуклость и вогнутость функции. Точки перегиба 55

Асимптоты 57

Список используемой литературы 63

Задания Вариант 1

1. Найти производную функции .

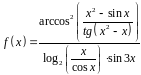2. Найти производные первого и второго порядка функции, заданной параметрически: .

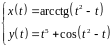3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции в точке .

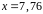5. Закон движения материальной точки имеет вид 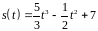. В какой момент времени скорость ее движения будет равна 42 м/с?

6. Исследовать функцию 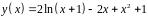и построить эскиз ее графика.

Вариант 2

1. Найти производную функции: .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

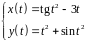3. Найти производную функции .

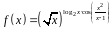4. С помощью дифференциала приближенно вычислить значение функции 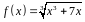в точке .

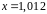5. Закон движения материальной точки имеет вид 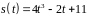. В какой момент времени скорость ее движения будет равна 190 м/с?

6. Исследовать функцию и построить эскиз ее графика.

Вариант 3

1. Найти производную функции: .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

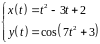3. Найти производную функции .

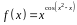4. С помощью дифференциала приближенно вычислить значение функции 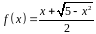в точке .

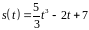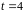5. Закон движения материальной точки имеет вид . Найти скорость ее движения в момент времени c.

6. Исследовать функцию 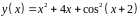и построить эскиз ее графика.

Вариант 4

1. Найти производную функции: .

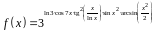2. Найти производные первого и второго порядка функции, заданной параметрически: .

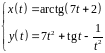3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции в точке .

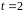5. Закон движения материальной точки имеет вид . Найти скорость ее движения в момент времени c.

6. Исследовать функцию 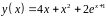и построить эскиз ее графика.

Вариант 5

1. Найти производную функции: .

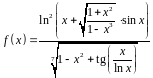2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции в точке .

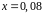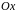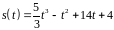5. По оси движутся две материальные точки, законы движения которых имеют вид и . В какой момент времени их скорости будут равными?

6. Исследовать функцию 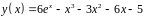и построить эскиз ее графика.

Вариант 6

1. Найти производную функции .

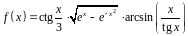2. Найти производные первого и второго порядка функции, заданной параметрически: .

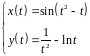3. Найти производную функции .

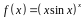4. С помощью дифференциала приближенно вычислить значение функции в точке .

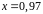5. Закон движения материальной точки имеет вид 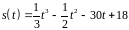. В какой момент времени скорость ее движения будет равна нулю?

6. Исследовать функцию 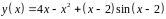и построить эскиз ее графика.

Вариант 7

1. Найти производную функции .

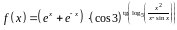2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

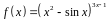4. С помощью дифференциала приближенно вычислить значение функции в точке .

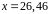5. Тело движется по прямой по закону 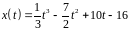. Определить скорость и ускорение движения тела. В какие моменты времени оно меняет направление движения?

6. Исследовать функцию 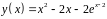и построить эскиз ее графика.

Вариант 8

1. Найти производную функции

.

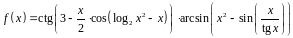2. Найти производные первого и второго порядка функции, заданной параметрически: .

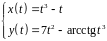3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции 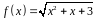в точке .

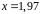5. Закон движения материальной точки имеет вид 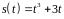. Найти скорость ее движения в момент времени с.

6. Исследовать функцию и построить эскиз ее графика.

Вариант 9

1. Найти производную функции .

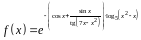2. Найти производные первого и второго порядка функции, заданной параметрически: .

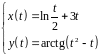3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции в точке .

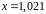5. Определить угловой коэффициент касательной к кривой 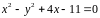в точке .

6. Исследовать функцию 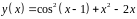и построить эскиз ее графика.

Вариант 10

1. Найти производную функции .

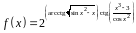2. Найти производные первого и второго порядка функции, заданной параметрически: .

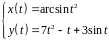3. Найти производную функции .

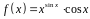4. С помощью дифференциала приближенно вычислить значение функции в точке .

5. В какой точке крив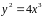ой касательная к графику ее функции перпендикулярна прямой ?

6. Исследовать функцию 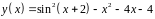и построить эскиз ее графика.

Вариант 11

1. Найти производную функции

.

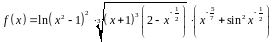2. Найти производные первого и второго порядка функции, заданной параметрически: .

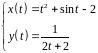3. Найти производную функции .

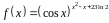4. С помощью дифференциала приближенно вычислить значение функции 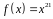в точке .

5. Записать уравнение касательной к кривой в точке с абсциссой .

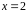6. Исследовать функцию 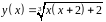и построить эскиз ее графика.

Вариант 12

1. Найти производную функции

.

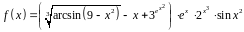2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

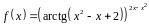4. С помощью дифференциала приближенно вычислить значение функции 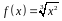в точке .

5. Записать уравнение касательной к кривой 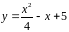в точке с абсциссой .

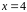6. Исследовать функцию 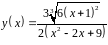и построить эскиз ее графика.

Вариант 13

1. Найти производную функции

.

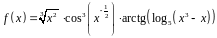2. Найти производные первого и второго порядка функции, заданной параметрически: .

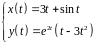3. Найти производную функции .

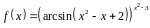4. С помощью дифференциала приближенно вычислить значение функции 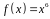в точке .

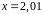5. Записать уравнение касательной к кривой в точке с абсциссой .

6. Исследовать функцию 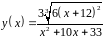и построить эскиз ее графика.

Вариант 14

1. Найти производную функции .

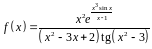2. Найти производные первого и второго порядка функции, заданной параметрически: .

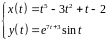3. Найти производную функции .

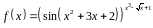4. С помощью дифференциала приближенно вычислить значение функции в точке .

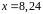5. Записать уравнение касательной к кривой 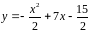в точке с абсциссой .

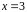6. Исследовать функцию и построить эскиз ее графика.

Вариант 15

1. Найти производную функции

.

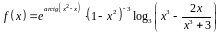2. Найти производные первого и второго порядка функции, заданной параметрически: .

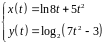3. Найти производную функции .

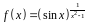4. С помощью дифференциала приближенно вычислить значение функции 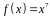в точке .

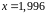5. Записать уравнение нормали к кривой 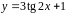в точке с абсциссой .

6. Исследовать функцию 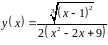и построить эскиз ее графика.

Вариант 16

1. Найти производную функции .

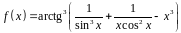2. Найти производные первого и второго порядка функции, заданной параметрически: .

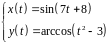3. Найти производную функции .

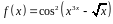4. С помощью дифференциала приближенно вычислить значение функции в точке .

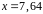5. Записать уравнение нормали к кривой в точке с абсциссой .

6. Исследовать функцию 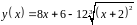и построить эскиз ее графика.

Вариант 17

1. Найти производную функции

.

2. Найти производные первого и второго порядка функции, заданной параметрически: .

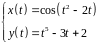3. Найти производную функции .

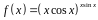4. С помощью дифференциала приближенно вычислить значение функции в точке .

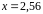5. Записать уравнение касательной к кривой 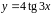в точке с абсциссой .

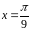6. Исследовать функцию 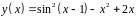и построить эскиз ее графика.

Вариант 18

1. Найти производную функции .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

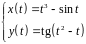3. Найти производную функции .

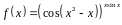4. С помощью дифференциала приближенно вычислить значение функции 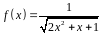в точке .

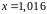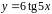
5. Записать уравнение нормали к кривой в точке с абсциссой .

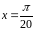6. Исследовать функцию 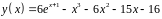и построить эскиз ее графика.

Вариант 19

1. Найти производную функции

.

2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

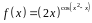4. С помощью дифференциала приближенно вычислить значение функции в точке .

5. Записать уравнение касательной к кривой в точке с абсциссой .

6. Исследовать функцию и построить эскиз ее графика.

Вариант 20

1. Найти производную функции .

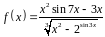2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

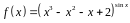4. С помощью дифференциала приближенно вычислить значение функции в точке .

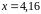5. Выяснить, в какой точке кривой касательная составляет с осью угол .

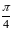6. Исследовать функцию 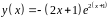и построить эскиз ее графика.

Вариант 21

1. Найти производную функции

.

2. Найти производные первого и второго порядка функции, заданной параметрически: .

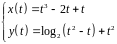3. Найти производную функции .

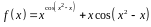4. С помощью дифференциала приближенно вычислить значение функции в точке .

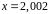5. Выяснить, в какой точке кривой касательная составляет с осью угол .

6. Исследовать функцию и построить эскиз ее графика.

Вариант 22

1. Найти производную функции .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

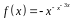4. С помощью дифференциала приближенно вычислить значение функции 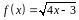в точке .

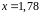5. Выяснить, в какой точке кривой касательная cоставляет с осью угол .

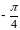6. Исследовать функцию 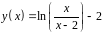и построить эскиз ее графика.

Вариант 23

1. Найти производную функции .

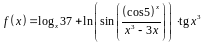2. Найти производные первого и второго порядка функции, заданной параметрически: .

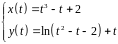3. Найти производную функции .

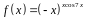4. С помощью дифференциала приближенно вычислить значение функции в точке .

5. Выяснить, в какой точке кривой 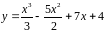касательная составляет с осью угол .

6. Исследовать функцию 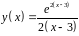и построить эскиз ее графика.

Вариант 24

1. Найти производную функции .

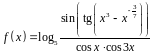2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

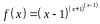4. С помощью дифференциала приближенно вычислить значение функции в точке .

5. Найти точки на кривой 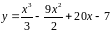, в которых касательные параллельны оси .

6. Исследовать функцию 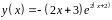и построить эскиз ее графика.

Вариант 25

1. Найти производную функции .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции 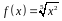в точке .

5. Найти точку на крив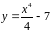ой , касательная в которой параллельна прямой .

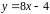6. Исследовать функцию 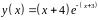и построить эскиз ее графика.

Вариант 26

1. Найти производную функции .

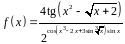2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

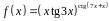4. С помощью дифференциала приближенно вычислить значение функции 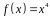в точке .

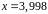5. Найти точку на крив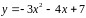ой , касательная в которой перпендикулярна прямой .

6. Исследовать функцию 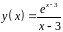и построить эскиз ее графика.

Вариант 27

1. Найти производную функции .

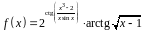2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции 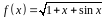в точке .

5. Найти точку на кривой , касательная в которой параллельна прямой .

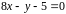6. Исследовать функцию и построить эскиз ее графика.

Вариант 28

1. Найти производную функции .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

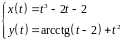3. Найти производную функции .

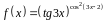4. С помощью дифференциала приближенно вычислить значение функции 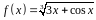в точке .

5. Найти точку на кривой 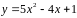, касательная в которой перпендикулярна прямой .

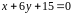6. Исследовать функцию и построить эскиз ее графика.

Вариант 29

1. Найти производную функции .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

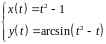3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции 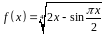в точке .

5. Найти точку на крив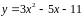ой , касательная в которой параллельна прямой .

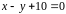6. Исследовать функцию 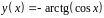и построить эскиз ее графика.

Вариант 30

1. Найти производную функции .

2. Найти производные первого и второго порядка функции, заданной параметрически: .

3. Найти производную функции .

4. С помощью дифференциала приближенно вычислить значение функции в точке .

5. Найти точку на крив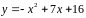ой , касательная в которой параллельна прямой .

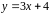6. Исследовать функцию 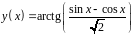и построить эскиз ее графика.

Вариант 31

1. Найти производную функции .

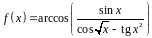2. Найти производные первого и второго порядка функции, заданной параметрически: .

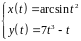3. Найти производную функции .

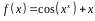4. С помощью дифференциала приближенно вычислить значение функции 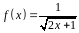в точке .

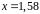5. Закон движения материальной точки имеет вид 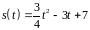. В какой момент времени скорость ее движения будет равна 2 м/с?

6. Исследовать функцию и построить эскиз ее графика.