3. Инструменты анализа временных рядов

В процессе построения временных рядов принято выделять следующие три элемента:

• Уровень автокорреляции (определение её порядка );

• Интегрированность (взятие последовательной разности порядка );

• Компонент скользящей средней (определение её порядка ).

Далее рассмотрим использование коэффициента автокорреляции (Auto-Correlation Coefficient — ACC) и частного коэффициента автокорреляции (Partial Auto-Correlation Coefficient — PACC) для идентификации элементов и в процессе построения модели временных рядов.

Для определения степени интегрирования воспользуемся расширенным тестом Дики-Фуллера

Коэффициент автокорреляции измеряет связь между текущими и прошлыми наблюдениями временных рядов и рассчитывается следующим образом:

, где

— количество лагов (может принимать значение от 1 до );

— коэффициент корреляции порядка ;

.

Таким образом, коэффициент автокорреляции первого порядка будет рассчитан с лагом в один период, то есть учитывать степень связи между значениями, отстоящими на один временной период.

Коэффициент автокорреляции второго порядка будет рассчитан с лагом в два периода, то есть учитывать степень связи между значениями, отстоящими на два временных периода.

Аналогично рассчитываются коэффициенты автокорреляции всех порядков. Затем проводится статистическая проверка для определения, при каких лагах коэффициенты статистически значимы.

Только лаги, являющиеся статистически значимыми, остаются в модели.

Графическое представление коэффициентов автокорреляции будем называть коррелограммой. Если коэффициентов значимы, то тогда коррелограмма быстро убывает до -того значения, то есть на коррелограмме значений будут ненулевыми, а потом быстро убывать до нуля.

Например: коррелограмма стационарного ряда быстро убывает после нескольких первых значений: Если же коррелограмма убывает медленно, то можно предположить нестационарность ряда.

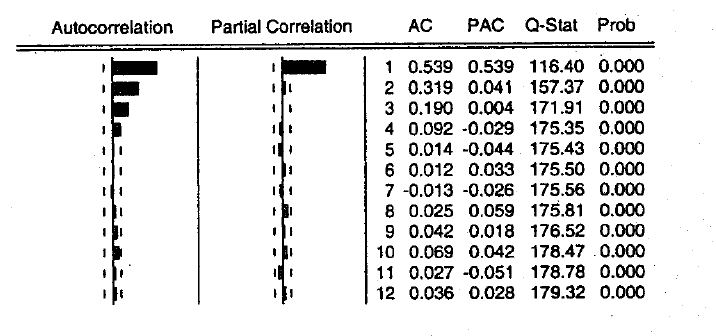
Рис.6 Коррелограмма стационарного ряда

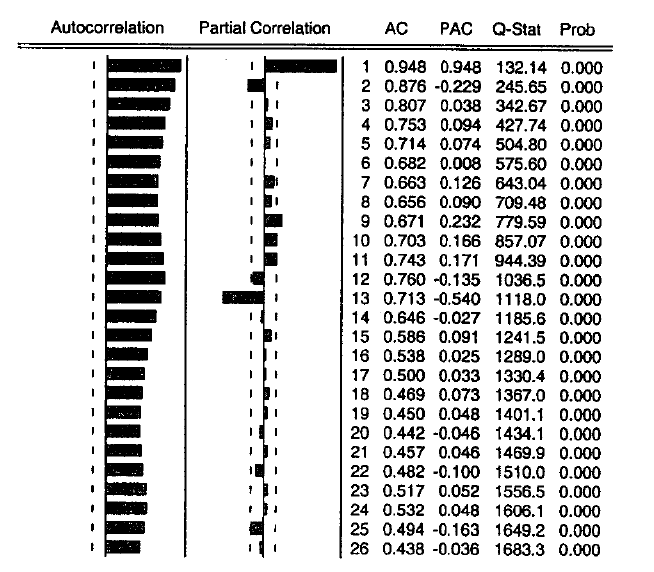
Рис.7 Коррелограмма нестационарного ряда — объем продаж пиротехники (Ряд включает тренд, сезонность и случайную компоненту)

Критерии для проверки значимости коэффициентов автокорреляции

Критерий стандартной ошибки служит для проверки значимости коэффициентов автокорреляции каждого порядка по отдельности:

,

где – размер выборки,

— выборочный коэффициент корреляции порядка .

Критерий Бокса-Пирса ( ) проверяет на значимость все множество коэффициентов как группу.

~ , где

— максимальный рассматриваемый лаг

n – объем выборки.

Два критерия предполагаются из-за существования двух подходов к проверке наличия автокорреляции, в зависимости от ситуации.

Пример: Пусть рассматриваются уровни цен и доходность британских государственных долгосрочных облигаций. Коэффициенты автокорреляции рассчитываются на основе выборки из 900 наблюдений. Тогда стандартная ошибка:

.

Построим гипотезу о равенстве нулю выборочного коэффициента автокорреляции и альтернативную для нее:

: (не значимы);

: (значимы).

Для проверки гипотезы в общем случае необходимо рассчитать значение -статистики. В случае большой выборки можно использовать -статистику (нормальное распределение):

.

Затем для проверки гипотезы на 5% уровне значимости (двухсторонний тест) необходимо сравнить посчитанное значение с критическим табличным значением статистики.

Если , принимается основная гипотеза . Иначе она отвергается.

,

,

,

.

Доверительный интервал будет выглядеть следующим образом:

Лаг,	Функция ACC,
1	0.095
2	0.012
3	0.074
4	-0.009
5	0.022
6	0.031
7	0.080
8	0.068
9	0.011

В данном случае рассматривается временной ряд цен облигаций. Значимыми оказываются коэффициенты корреляции с лагами 1, 3, 7, 8 — . Таким образом, на сегодняшний уровень цен влияют цены, отстающие на 1, 3, 7, 8 лагов (дней, недель, месяцев, лет и так далее).

Построим критерий Бокса-Пирса:

~ , где

— максимальный рассматриваемый лаг (в данном примере ). В нашем случае Q-статистика будет иметь следующее значение:

.

Сравним с .

, значит как группа коэффициенты для лагов в девять периодов являются значимыми.

Частный коэффициент автокорреляции (PACC)

Измеряет связь между текущим значением переменной и лаговыми значениями переменной , когда влияние всех промежуточных переменных устранено (аналог — условная вероятность, условный экстремум). Таким образом частный коэффициент автокорреляции первого порядка будет равен коэффициенту корреляции первого порядка ( ), так как нет промежуточных лагов.

Но ( ), при .

В динамическом процессе частные коэффициенты автокорреляции значимо отличаются от нуля для временных лагов от 1 до р (то есть ). А затем резко падают до нуля.

Если значения частного коэффициента автокорреляции падает по экспоненте, а не опускается резко до нуля, то можно предположить, что ряд содержит процесс скользящей средней (MA).

Критерий для ARMA процессов. Критерий Люнга-Бокса (Ljung-Box, 1978 г.)

Для проверки автокорреляции в рядах, где присутствуют элементы и автокорреляции, и скользящей средней.

Статистика LB:

 , где

— максимальное число временных лагов, рассматриваемых в модели;

— порядок авторегрессии ;

— порядок скользящей средней .

Проверка степени интеграции

Процесс интеграции используется для того, чтобы преобразовать ряд в стационарный с помощью разностей разного порядка. Так как многие методы анализа временных рядов подразумевают, что анализируемый ряд в действительности является стационарным и тогда можно использовать обычный МНК.

Степень интеграции проверяется с помощью критерия Дики-Фуллера (D. A. Dickey, W. A. Fuller, 1976 г., DF-статистика). С помощью этого подхода проверяется, значимо ли отличается коэффициент от единицы в уравнении:

(6),

~ .

Если , то ряд (6) — неустойчивый (случайное блуждание);

В финансах обычно не бывает больше единицы, поскольку это подразумевает взрывные ряды (кризис, дефолт). Такие ряды маловероятны, поскольку давление экономической среды не позволяет переменной принять бесконечно большие значения (см. «Рынок ценных бумаг. Учебное пособие» Пахомов А.В., Пахомова Е.А. стр.69 Влияние рынка опционов на экономическую систему в целом).

Обозначение — описывает интегрированность первого порядка ( ),

— ряд стационарен ( ).

Уравнение (6) для удобства анализа можно преобразовать к следующему виду:

.

Проверим гипотезу о равенстве единице коэффициента :

: ,

обозначим , , тогда

.

обозначим , тогда

(6’).

В таком случае гипотеза : эквивалентна гипотезе : .

Из уравнения (6) следует, что выполняется условие устойчивости. В уравнении (6) и (6’) нет константы и нет тренда. В финансовых рядах часто уместно включить положительную среднюю, потому что рисковые активы подразумевают положительную норму прибыли. Тогда вместо (6) и (6’):

(7),

или (7’).

Третья форма уравнения, уместная в финансах имеет тренд:

(8),

или (8’).

,

или, если записать иначе ,

.

Как показали Дики и Фуллер в случае, если (то есть ) -статистика не распределена по Стьюденту и её распределение не стремится к стандартному нормальному при увеличении размера выборки .

Распределение -статистики при условии ( ) описано Дики и Фуллером для уравнений (6) — (8).

В таблице приведены односторонние критические значения статистики DF для некоторых размеров выборки.

Уровни значимости, p	Размер выборки, n
	25	50	100
	AR-модель (1)
0,025	-2,26	-2,25	-2,24	-2,23
0,050	-1,95	-1,95	-1,95	-1,95
	AR-модель с константой (2)
0,025	-3,33	-3,22	-3,17	-3,12
0,050	-3,00	-2,93	-2,89	-2,86
	AR-модель с трендом и константой (3)
0,025	-3,95	-3,80	-3,69	-3,66
0,050	-3,60	-3,50	-3,45	-3,41

Пример: допустим мы тестируем гипотезу : ( ) для AR-модели с константой (2) при наблюдениях и уровнем значимости 5%. Тогда -статистика равна:

.

Однако, согласно Дики-Фуллеру , то есть гипотеза H₀ реже отвергается при использовании таблицы Дики-Фуллера, чем при использовании таблицы Стьюдента, что может послужить причиной ошибки.

Интересным фактом является то, что критические значения DF остаются справедливыми при статистическом анализе уравнений (6’) — (8’). Тест, соответствующий уравнению с логированными разностями ( ) называется расширенным тестом Дики-Фуллера (augmented DF — ADF).

Модель распределенных лагов (DL)

Эта модель имеет вид:

(9),

.

В случае, когда — детерминированные переменные, а ошибки ~ , то модель (9) удовлетворяет условиям классической линейной регрессии.

Однако на практике при ее оценивании могут встретиться трудности:

• количество коэффициентов , которое требуется оценить, может оказаться слишком велико, если по смыслу задачи ожидается влияние с большим запаздыванием;

• если ряд переменных имеет некоторую структуру (например, сезонность), то тогда это будет означать, что лагированные объясняющие переменные сильно коррелированны между собой, а значит мы попадаем в ситуацию мультиколлинеарности.

Подробнее: матрица данных , где , будет состоять из столбцов, некоторые из которых линейно зависимы между собой, тогда ранг такой матрицы будет меньше чем ее размерность, из чего следует, что ее детерминант близок к нулю, то есть матрица близка к вырожденной, а значит, классический метод МНК не применим.

Для преодоления этих трудностей используют модели, которые приводят к уменьшению числа оцениваемых параметров:

• модели полиномиальных лагов, которые решаются методом Алмона (Almon);

• модели геометрических лагов, которые решаются моделью Койка (Koyck).

Модель полиномиальных лагов

В этой модели коэффициенты из модели (9) считаются функцией от ( ) и аппроксимируются полиномом некоторой степени :

, где (10).

После подстановки (10) в (9) получаем модель, содержащую только неизвестных параметров. Покажем это:

Обозначим:

Таким образом получаем:

(11),

где переменные являются линейными комбинациями переменных , и количество коэффициентов теперь равно .

Чтобы определить порядок полинома требуется ответить на вопрос, каково качество модели (11) по сравнению с качеством модели (9). За качество модели отвечает сумма квадратов остатков (Error Sum of Squares, ESS). Будем обозначать (регрессия без ограничений, unrestricted) для модели (9) и — регрессия с ограничениями, то есть restricted для модели (11) тогда качество модели будет определяться с помощью -статистики:

;

~ .

Числитель — это изменение суммы квадратов остатков в расчете на один отсутствующий параметр. В знаменателе — сумма квадратов остатков в регрессии без ограничений, приходящуюся на одну степень свободы.

Таким образом для того, чтобы модель была хорошей должно выполняться соотношение:

,

Так как числитель не должен отличаться значимо от нуля.

Модель геометрических лагов

В этой модели предполагается, что влияние переменной убывает на один и тот же процент с каждым шагом. Модель имеет вид:

(12),

где .

Модель содержит только три параметра , однако, её оценивание осложняется тем, что коэффициент однозначно оценить не удается. В самом деле, можно получить как коэффициент при или возвести в квадрат коэффициент при , или, возведя коэффициент при в квадрат, и разделить его на коэффициент при . То есть существует много различных и противоречивых способов, поскольку все они будут давать различные значения .

Оценку этой модели можно произвести например с помощью процедуры Хилдреда-Лу (Hildreth-Lu). Перебирая с некоторым шагом значения и для каждого находим МНК-оценки уравнения (12). В результате такой процедуры оценивание сводиться к оцениванию парной регрессии и можно найти и . Из всех регрессий выбирается такая регрессия с таким , при котором . Есть и другие способы оценивания этой модели, однако они требуют метода максимального правдоподобия.

1