Лекция 7. Многокритериальная оптимизация

7.1 Общие положения обоснования критериев оптимизации с позиции компромисса.

Методы принятия компромиссных решений широко применяются в практике оптимизации многокритериальных задач. Обычно решение задачи многокритериальной оптимизации заключается в поиске наилучшего компромиссного решения [**,**].

В области компромиссных решений нельзя достигнуть одновременного улучшения решения по всем критериям. Область компромиссов является областью оптимальных решений по Парето (итальянский специалист в области политической экономии капитализма). При этом оптимальными по Парето являются решения, имеющие по всем критериям не худшие, а по одному из них лучший показатель, чем другие альтернативы. Выделение решений, оптимальных по Парето, обычно позволяет сократить количество рассматриваемых альтернатив.

Покажем формирование области компромиссных решений на примере определения оптимального значения одной непрерывной переменной по двум критериям (рис. 7.1)

Рис. 7.1 Формирование области компромиссных решений на примере определения оптимального значения одной непрерывной х переменной по двум критериям: К₁ и К₂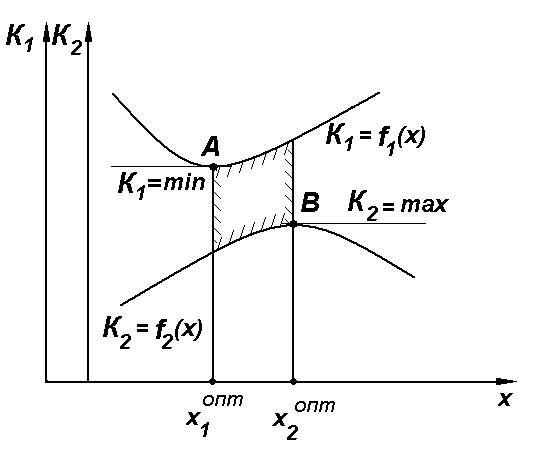

По первому критерию оптимальным решением является х₁^opт, которое соответствует минимуму функции f₁(х) в точке А, по второму – х₂^opт, соответствующее максимуму функции f₂(х). Оптимальные значения оптимизируемой переменной заключены на отрезке оси абсцисс между локальными по одному из критериев оптимами х₁^opт и х₂^opт. Заштрихованная область между вертикальными линиями, проходящими через точки экстремальных значений целевых функций и ограниченная сверху и снизу графиками целевых функций К₁ = f₁(х) и К₂ = f₂(х), является областью компромиссов.

Критериев в многокритериальных задачах может быть значительно больше. Рассмотрим общие положения в решении таких задач.

Сначала определяются критерии оптимизации в порядке их важности: W₁, W₂, W₃,..., W_n.

Будем считать, что каждый из них нужно обратить в минимум или максимум. Сначала найдем решения, обращающие в минимум (максимум) главный критерий оптимизации W₁.

Следующей операцией является назначение некоторой «уступки» ΔW₁, которую, исходя из практических соображений и точности, можно допустить для уменьшения (увеличения) второго критерия – W₂.

На значения параметра W₁ накладываются ограничения:

.

(7.1)

С учетом (7.1) находится наименьшее (наибольшее) значение критерия W₂.

Далее такую операцию осуществляют для оставшихся критериев W₃, W₄,…,W_n.

Положительной стороной этого подхода является наглядность того, ценой какой «уступки» в одном показателе приобретается выигрыш в другом.

Недостатком данного метода, как и вообще всех компромиссных методов, является субъективность.

Общей проблемой в решении многокритериальных задач является то, что отдельные критерии нельзя свернуть в единый отклик, т.к. критерии имеют различную природу и, следовательно, различную размерность. Поэтому необходимо привести все частные критерии к одной размерности или сделать их безразмерными.

Различают три основных подхода в принятии компромисса.