Лекция 6. Системный анализ при оптимизации инвестиций в геологоразведочные работы

6.1 Общая постановка динамической задачи оптимизации

В экономических задачах, организации и управления производством управление обычно заключается в оптимальном распределении на каждом этапе производственных заданий, ресурсов, финансов и т.д. При этом этапом планирования (решения задачи) является временной отрезок (год, сутки, месяц и т.д.), т.е. большинство задач планирования и управления являются динамическими.

Например, планируется работа геологоразведочного объединения, включающего ряд производственных единиц П₁, П₂,…,П_i,…,П_к на период времени t = 1,2,…, Т лет.

В начале периода (состояние S_о) система характеризуется определенным количеством оборотных и основных фондов, трудовыми ресурсами и т.д. На развитие объединения дополнительно выделено К средств, которое определяет конечное состояние системы S_к.

Необходимо так распределить дополнительные средства по годам и производственным единицам, чтобы к концу рассматриваемого периода Т суммарный доход объединения W был бы максимальным.

Управляемые переменные х_it – количество средств выделенное i-му предприятию в год t.

Распределение средств по производственным единицам в год t – x_1t, x_2t,…,x_it,…,x_кТ характеризует управление на этапе t – u_t.

Совокупность управлений по годам выразится системой:

u1(x11, x21,…,xk1), u2(x12, x22,…,xk2), ………………..…, ut(x1t, x2t,…,xkt), …………….……., uT(x1T, x2T,…,xkT).

(6.1)

Каждому распределению средств по годам соответствует определенный доход w_t, причем общий доход W за Т лет зависит от совокупности управлений, т.е.

.

(6.2)

Итак, задача состоит в определении управления на каждом этапе, чтобы общий доход геологоразведочного объединения был максимален. Найдя оптимальное управление на каждом этапе t=1, 2,…, Т (в каждый год), мы найдем и оптимальное решение всей задачи.

В динамических задачах из множества допустимых управлений u=(u₁, u₂,…,u_t,…,u_T) надо найти оптимальное, при котором система переходит из начального состояния в конечное таким образом, что процесс протекает наиболее эффективно (т.е. критерий оптимальности W достигает максимума или минимума).

Общую математическую постановку динамической оптимизационной задачи можно представить следующим образом:

W=w (x₁,u₁)+…+w (x_t,u_t)+…+w (x_T,u_T)max, (6.3)

x_t+1=f(x_t,u_t), , (6.4)

{x_t,u_t} , (6.5)

где х_t – вектор состояния, а u_t – вектор управления.

Выражение (6.4) показывает, что последующее состояние х_t+1 определяется предшествующим x_t и управлением u_t на данном этапе.

В частных случаях условия (6.5) могут представлять ограничения на вектор управления u_tU_t и вектор состояния x_tX_t.

6.2 Геометрическая интерпретация динамической задачи оптимизации

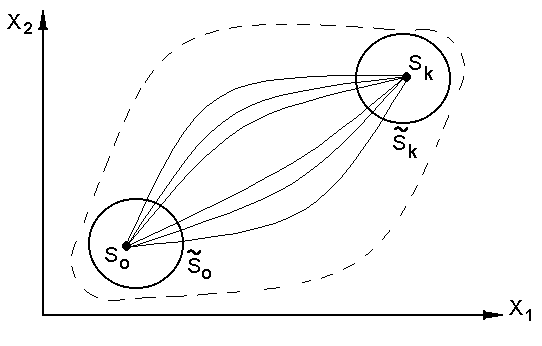
Динамическая задача оптимального управления имеет следующую геометрическую интерпретацию (рис. 6.1). Найти такую траекторию перемещения точки S в фазовом пространстве, при которой перемещение точки из начального состояния S_о в конечное S_к произойдет внутри области возможных состояний системы и критерий эффективности W примет оптимальное значение.

Рис. 6.1 Графическая интерпретация задачи динамического программирования

Фазовое пространство – это область, в которой находятся возможные траектории перемещения точки из начального состояния S_о в конечное S_к.