5.2 Графическое решение системы линейных ограничений

Линейное программирование как метод системного анализа рассмотрим на примере графического решения системы линейных ограничений.

Пусть требуется решить систему линейных ограничений (5.2).

Z=x1+x2+1max 5x1+x2  5; 3x1+2x2  6; x1–0.5x2  3; x1+ 2x2  8; x1, x2  0.

(5.2)

Приведем задачу к каноническому виду, введя в каждое неравенство вспомогательную неотрицательную переменную, и решим полученную систему уравнений. После чего исходная задача будет иметь вид (5.3):

Z=x₁+x₂+1 max

y₁= 5x₁+x₂ – 5  0;

y₂=3x₁+2x₂ –6  0; (5.3)

y₃=–x₁+0.5x₂+ 3  0;

y₄= –x₁ – 2x₂ + 8  0.

Рис. 5.1 Графическое решение системы ограничений (4.3), имеющее единственное максимальное значение.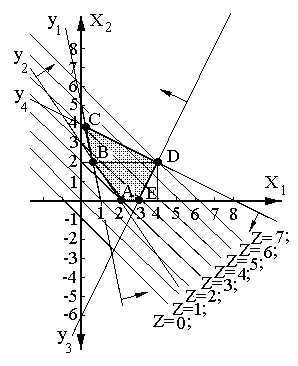

В положительном октанте системы координат х₁, 0, х₂ (рис. 5.1) построим полуплоскости, соответствующие решениям неравенств, и выделим область их пересечения.

Для того, чтобы построить полуплоскость, соответствующую решению неравенства x₁+x₂  5, запишем его в виде уравнения x₁+x₂ = 5, поскольку знак отношения позволяет это сделать. График линейной функции x₁+x₂ = 5 легко построить по двум точкам. При х₁=0; х₂=5. При х₂=0; х₁=1. Область возрастания показана стрелкой. Аналогично строятся полуплоскости, соответствующие решениям остальных трех неравенств. На рис. 5.1 показана выделенная выпуклая область решений ABCDE.

Построим линии уровня целевой функции, покрывающий полученный многогранник решений. Предположим, что целевая функция Z=x₁+x₂+1 имеет значение, равное нулю. Тогда ее можно записать в виде функции х₁+х₂ = – 1. График этой функции легко построить по двум точкам. При х₁=0; х₂= –1. При х₂=0; х₁= –1. Параллельно этому графику будут проходить и все остальные линии уровня целевой функции. Так линия уровня целевой функции, проходящая через начало координат, будет иметь значение Z=1. Следующая расположенная над ней линия уровня целевой функции будет иметь значение Z=2. Таким образом, видно в какую сторону происходит рост целевой функции. Нас интересуют линии уровня целевой функции, покрывающие положительный актант Эвклидова пространства.

Из рисунка видно, что целевая функция достигает максимального значения Z=7 в точке пересечения D линии y₃,y₄, т.е. в вершине многогранника решений при х₁=4 и при х₂=2. При этом выполняются все ограничения.

Из обобщения геометрического решения задачи ЛП на многомерный случай вытекает важнейшая для численного решения теорема о том, что линейная функция задачи ЛП достигает своего единственного максимального значения в крайней точке множества решений. Отсюда следует очень важный вывод, оптимальное решение основной задачи ЛП следует искать среди допустимых базисных решений системы ограничений. В дальнейшем допустимое базисное решение основной задачи ЛП будет называться опорным.

Рис. 5.2 Графическое решение системы ограничений (4.4), когда оптимум достигается в двух и более крайних точках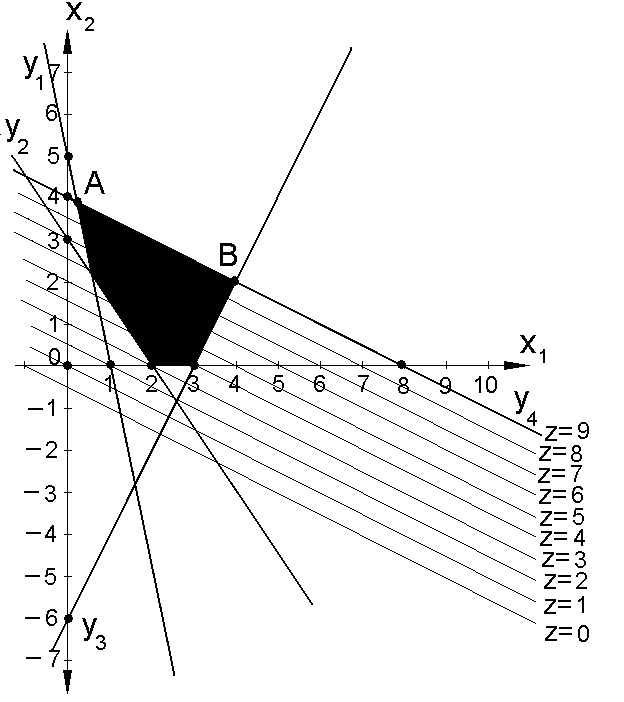

Если еще раз обратиться к вышеприведенному рисунку, то может возникнуть мысль, что при определенных условиях коэффициентов целевой функции линии уровня могут стать параллельны ребру y₄ или y₃ и тогда оптимальное решение станет не единственным. Рассмотрим систему ограничений (5.4).

Z=x₁+2x₂+1 max

5x₁+x₂  5;

3x₁+2x₂  6; (5.4)

x₁–0.5x₂  3;

x₁, x₂  0.

Графическое решение системы ограничений иллюстрирует рис. 5.2.

Здесь целевая функция достигает максимального значения Z=9 не только в вершинах многоугольника А и В, но и во всех точках ребра АВ.

Этот пример показывает, что при решении задачи ЛП может возникнуть случай, когда оптимум достигается в двух и более крайних точках и тогда он достигается и во всех остальных точках, являющихся их выпуклой линейной комбинацией.

Приведем пример, когда решение может оказаться неограниченным.

Рассмотрим систему ограничений (5.5):

Z=x1+x2+1 max 5x1+x2  5; 3x1+2x2  6; x1–0.5x2  3; x1, x2  0.

(5.5)

Графическое решение системы ограничений иллюстрирует рис. 5.3.

Рис. 5.3 Графическое решение системы ограничений (5.5), когда целевая функция неограниченна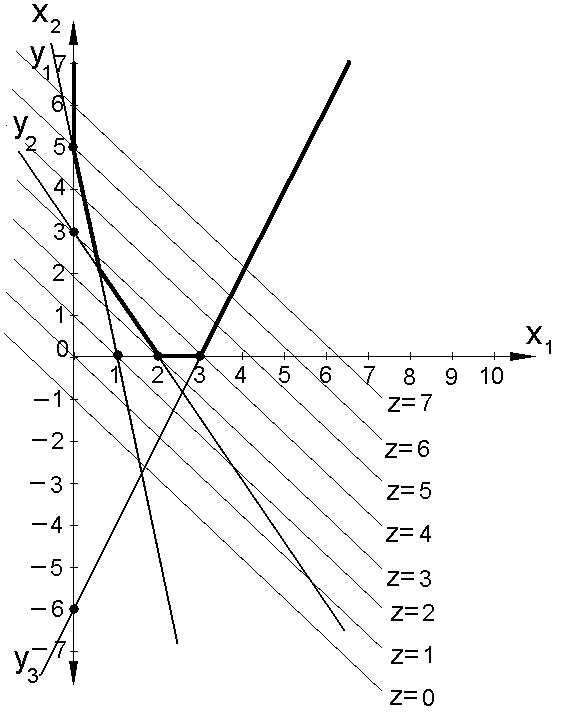

Здесь целевая функция не имеет условного максимума, т.к. многогранник решений незамкнут в направлении роста целевой функции. В этом случае говорят, что целевая функция неограниченно.

Приведем пример системы ограничений (5.6), который отличается от примера (предыдущего) только целевой функцией.

Z=x₁+x₂+1 max

5x₁+x₂  5;

3x₁+2x₂  6; (5.6)

x₁–0.5x₂  3;

x₁, x₂  0;

Графическое решение системы ограничений иллюстрирует рис. 5.4.

Она имеет единственное оптимальное решение х₁=2; х₂=0; Z= –1, т.к. в данном случае многогранник решений замкнут в направлении роста целевой функции.

Если обобщить результаты исследований графических решений систем ограничений (5.3)…(5.5), то можно сделать следующие выводы:

1. Оптимальное решение следует искать среди допустимых базисных решений системы ограничений, т.е. опорных решений.

2. При неограниченном множестве решений целевая функция может бесконечно возрастать (пример – система ограничений (5.5)).

Рис. 5.4 Графическое решение системы ограничений (4.6), когда многогранник решений замкнут в направлении роста целевой функции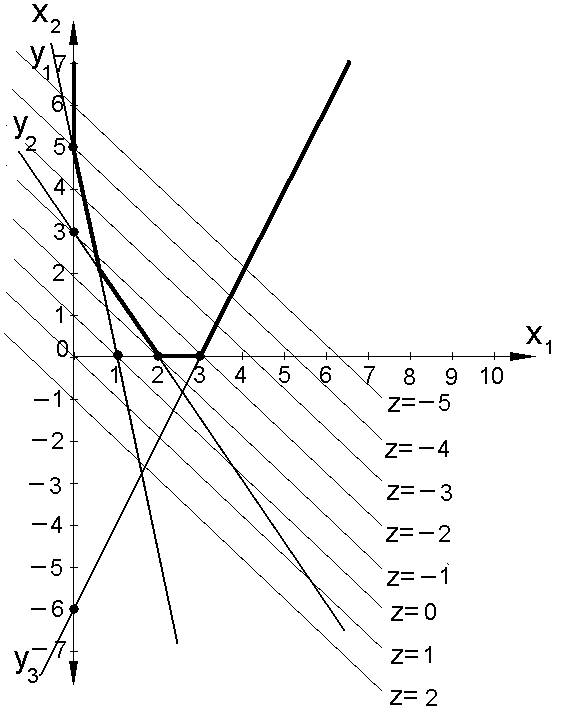

3. Оптимальное решение может быть неединственным, но при этом максимум целевой функции существует хотя бы в двух опорных решениях (пример – система ограничений (5.4)).

Кроме этого задача ЛП может иметь несовместную систему ограничений, если ограничения противоречат друг другу.

После того, как полностью определены возможные исходы решения задачи и возможные точки оптимума, можно выбирать стратегию поиска.

Целенаправленность поиска должна обеспечивать рост целевой функции. Отсюда вытекает еще одно условие стратегии поиска: при переходе от одного опорного решения к другому должен обеспечиваться рост целевой функции.

Данная стратегия направленного поиска предполагает наличие некоторого исходного опорного решения, поэтому весь процесс решения распадается на три этапа:

– поиск исходного базисного решения (на рис. 5.1 это – точка, находящаяся в положительном актанте, но не лежащая внутри многоугольника ABCDE , представляющего собой область возможных допустимых решений);

– поиск опорных решений (на рис. 5.1 это – точки, находящиеся в какой-нибудь из вершин многоугольника ABCDE, но значения целевой функции в них меньше максимального);

– поиск оптимального решения (на рис. 5.1 это – точка, находящаяся в вершине D многоугольника ABCDE, в которой значение целевой функции максимально.

Если задачу с двумя элементами решения можно решить графически (плоская задача), то наличие в линейной модели большего количества элементов решения требует использования аналитического метода решения (симплекс-метода). В настоящее время есть стандартные программы на ЭВМ, позволяющие реализовывать данный метод.