Контрольная работа № 1

по математике

для студентов ИНЭК (заочное отделение)

специальностей М, ГМУ, УП

1 курс, I семестр

Методические указания по выполнению контрольной работы

В соответствии с учебным планом студенты-заочники ИНЭК выполняют задания контрольной работы № 1.

Каждый студент выполняет один вариант контрольной работы № 1. Выбор варианта осуществляется по сумме последних 3-х цифр номера зачетки, причем если в сумме получилось число N, больше 25, то студенты выполняют N-25 вариант. Например, номер зачетки студента № 057809, сумма последних трех цифр 17, следовательно, студент выполняет вариант № 17. Если номер зачетки № 067899, сумма последних трех цифр 26, следовательно, студент выполняет вариант № 1.

Выполняя контрольную работу, студент-заочник должен руководствоваться следующим:

1. Контрольные работы необходимо сдавать на рецензию в сроки, установленные графиком учебного процесса.

2. Контрольную работу следует выполнять в отдельной тетради в клетку (12 или 18 листов). Обложка тетради оформляется по образцу, который нужно получить у методиста.

3. Если при защите контрольной работы преподавателем будет установлено, что контрольная работа выполнена несамостоятельно, или содержит задачи не своего варианта, то она не будет зачтена и студент должен будет или дать все необходимые пояснения по решенным задачам, или выполнить новую контрольную работу по своему варианту.

4. К зачету (экзамену) студент допускается только с зачтенной контрольной работой.

Вопросы для подготовки к зачету (экзамену)

I семестр.

1. Матрицы и действия над ними. Обратная матрица. Ранг матрицы.

2. Определители и их свойства. Решение систем линейных уравнений методом Крамера.

3. Ранг матрицы. Решение систем линейных уравнений методом Гаусса.

4. Векторы (основные понятия) и действия над ними. Скалярное произведение. Векторное произведение. Смешанное произведение.

5. Уравнения прямой на плоскости (общее, каноническое, проходящей через две точки, параметрическое, с угловым коэффициентом). Взаимное расположение двух прямых. Расстояние от точки до прямой.

6. Кривые 2-го порядка на плоскости.

7. Уравнения прямой и плоскости в пространстве. Расстояние от точки до плоскости.

8. Понятие функции, область определения, основные элементарные функции. Классы функций.

9. Предел бесконечной числовой последовательности, предел функции одной переменной.

10. Бесконечно малые и бесконечно большие величины и их свойства. Эквивалентные бесконечно малые.

11. Основные теоремы о пределах. Замечательные пределы.

12. Непрерывность функции одной переменной в точке и на интервале. Свойства непрерывных функций. Точки разрыва и их классификация.

13. Понятие производной функции. Геометрический и физический смысл производной.

14. Основные правила дифференцирования. Таблица производных.

15. Дифференциал функции одной переменной, его геометрический смысл.

16. Производные и дифференциалы высших порядков.

17. Приложения производной к исследованию функций и построению графиков: интервалы монотонности, экстремумы, выпуклость, точки перегиба.

Рекомендуемая литература

1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., 1995.

2. Щипачев В.С. Высшая математика. М., 2001.

3. Высшая математика для экономистов. Под редакцией Кремера Н.Ш., М., 1997.

4. Сборник задач по высшей математике для экономистов. Под редакцией Ермакова В.И. М., 2002.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. М., 2001.

Методические указания при подготовке к выполнению контрольной работы

1. Вычисление определителей

1.1. Определители второго порядка

Определителем второго порядка называется число:

.

Определение показывает несложность вычисления определителей второго порядка.

Примеры.

1.2. Определители третьего порядка

Определителем третьего порядка называется число, которое может быть вычислено по следующему правилу (правило Саррюса): к определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:

_.

Примеры.

а) -

-15-24-24=0

б)

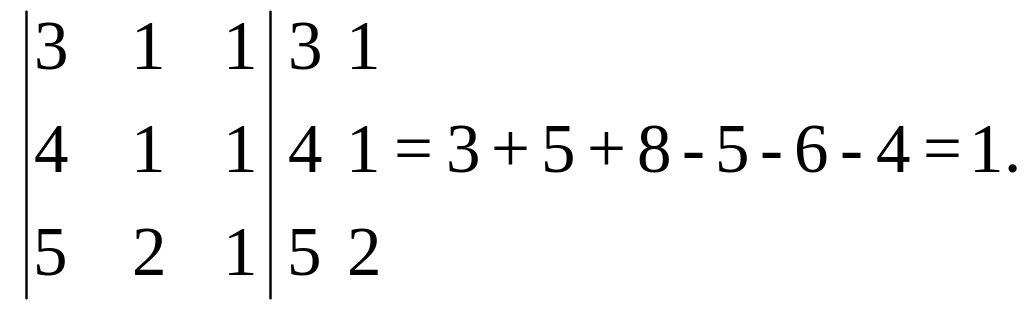
3. Задачи для самостоятельного решения

Вычислить определители второго и третьего порядка:

а) б) ; в)