3.2.2. Синтез регуляторов вентильных электроприводов

Задача синтеза регуляторов вентильных электроприводов рассматривается в данном параграфе на примере электропривода с двухфазным вентильным двигателем. При использовании трёхфазных вентильных двигателей задача синтеза регуляторов может быть решена аналогично после приведения трёхфазного двигателя к двухфазному.

Для решения задачи синтеза регуляторов требуется динамическая модель двухфазного вентильного двигателя. Ранее, в курсе электрических машин было показано, что двухфазный вентильный двигатель описывается следующей системой дифференциальных уравнений:

, (3.6)

, (3.7)

, (3.8)

, (3.9)

, (3.10)

, (3.11)

, (3.12)

где – потокосцепления статорных обмоток и соответственно; – соответственно токи и напряжения обмоток и ; – активное сопротивление статорных обмоток и ; – индуктивность статорных обмоток и ; – максимальное взаимное потокосцепление обмотки (или ), обусловленное ротором, выполненным в виде постоянного магнита; p – количество пар полюсов; – геометрический угол между продольными магнитными осями ротора и обмотки , отсчитываемый против часовой стрелки от оси обмотки к оси ротора; J – сумма моментов инерции вала двигателя и приведённого момента инерции нагрузки; – угловая скорость вращения вала двигателя; – соответственно электромагнитный (вращающий) момент двигателя и приведённый статический момент сопротивления нагрузки.

Непосредственное использование уравнений (3.6) – (3.12) для синтеза регуляторов невозможно. Для решения данной задачи, как и в случае асинхронного двигателя, требуется выполнить преобразование естественных переменных в переменные синхронной системы координат. Будем полагать, что синхронная система координат совпадает с осями d и q, введёнными при рассмотрений вентильного двигателя. Ось d, напомним, направлена по продольной оси ротора, а ось q – по поперечной оси ротора. Тогда следует считать, что

, (3.13)

где – угол поворота синхронной системы координат. Уравнения координатных преобразований в этом случае приобретают вид:

, (3.14)

, (3.15)

, (3.16)

, (3.17)

, (3.18)

, (3.19)

где – статорные соответственно напряжения, токи и потокосцепления в синхронной системе координат (d, q).

Напомним геометрический смысл записанных координатных преобразований на примере преобразований токов и . Нетрудно показать, что если токи и рассматривать как проекции некоторого вектора , расположенного под углом к продольной магнитной оси обмотки или, иначе говоря, по продольной оси ротора, то в координатах (d,q) этот вектор имеет координаты соответственно и . Вектор можно рассматривать, очевидно, как МДС некоторой воображаемой обмотки с единичным витком, продольная магнитная ось которой располагается по продольной оси ротора и, следовательно, вращается вместе с ротором.

Перейдём к подстановке (3.14) – (3.19) в (3.6) – (3.12). Но предварительно вычислим производные и с учетом того, что величины и задаются координатными преобразованиями (3.18) и (3.19). Дифференцируя величины и как сложные функции, получаем:

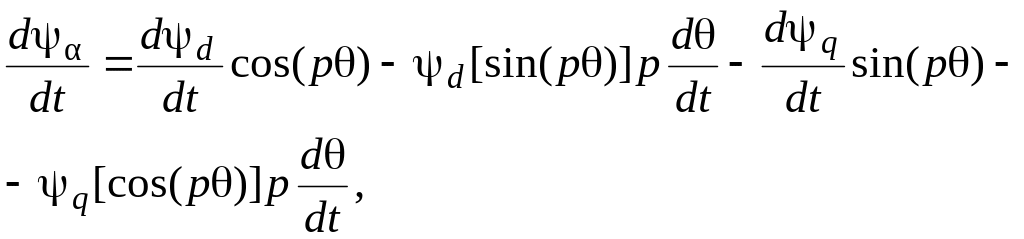(3.20)

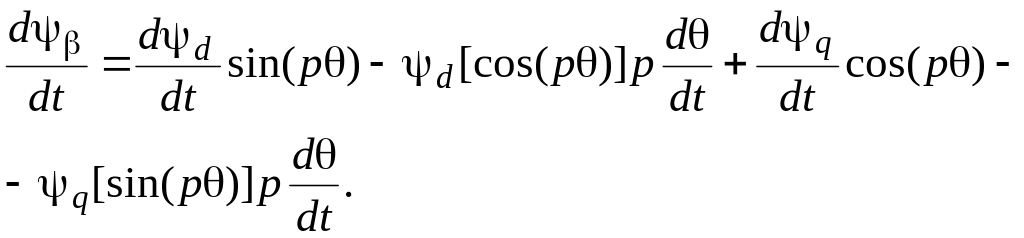(3.21)

Выполним преобразование равенств (3.6) и (3.7). Подставляя (3.20), (3.14) и (3.16) в (3.6), а также (3.21), (3.15) и (3.17) в (3.7), получаем с учётом замены , которая справедлива в силу (3.11), следующую систему уравнений:

(3.22)

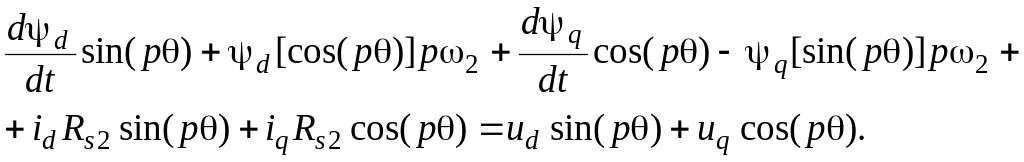(3.23)

Выполним преобразование равенств (3.8) и (3.9). Представляя (3.18) и (3.16) в (3.8), а (3.19) и (3.17) в (3.9), получаем:

, (3.24)

. (3.25)

Упростим равенства (3.22) и (3.23) следующим образом. Вначале умножим (3.22) на cos(p ) и (3.23) на sin(p ), а затем полученные равенства сложим, в результате чего после преобразований получим, что

. (3.26)

Далее умножим (3.22) на [-sin(p )] и (3.23) на cos(p ), а затем полученные равенства сложим, в результате чего после преобразований получим, что

. (3.27)

Упростим равенства (3.24) и (3.25). Вначале умножим (3.24) на cos(p ) и (3.25) на sin(p ), а затем полученные результаты сложим, в результате чего получим, что

. (3.27а)

Далее умножим (3.24) на [- sin(p )] и (3.25) на cos(p ), а затем полученные равенства сложим, в результате чего получим, что

. (3.27б)

Итак, после координатных преобразований исходных уравнений (3.6) – (3.9) приходим к уравнениям (3.26) – (3.27б), которые не содержат периодических коэффициентов.

Продолжим преобразование оставшихся исходных уравнений двигателя (3.10) – (3.12). Уравнения (3.10) и (3.11), очевидно, не изменяются координатными преобразованиями, а уравнение (3.12) после подстановки в него (3.16) и (3.17) преобразуется к виду

.

Таким образом, на основании изложенного приходим к выводу, что уравнения вентильного двигателя в синхронной системе координат имеют следующий вид:

, (3.28)

, (3.29)

, (3.30)

, (3.31)

, (3.32)

, (3.33)

. (3.34)

Продолжим упрощение уравнений вентильного двигателя. С этой целью в уравнениях (3.28) – (3.34) исключим, во-первых, потокосцепления и . Во-вторых, будем полагать для простоты, что вентильный электропривод регулирует только угловую скорость , т.е. не предназначен для регулирования угла . Тогда из уравнений двигателя может быть исключено уравнение (3.33) для угла , т.к. эта величина не входит в другие уравнения вентильного двигателя, записанные в синхронных координатах. С учётом изложенного уравнения (3.28) – (3.34) преобразуются к виду:

, (3.35)

, (3.36)

, (3.37)

. (3.38)

Из уравнения (3.38) следует, что электромагнитный момент М_э не за­висит от тока , т.е. этот ток не создает полезных усилий на валу двига­теля. Ясно, однако, что ток создает электрические потери в обмотках двигателя, протекая по их активным сопротивлениям . Возникает сле­дующая идея: при управлении угловой скоростью застабилизировать ток на нуле­вом уровне, чтобы снизить электрические потери в двигателе.

Из изложенного, таким образом, следует, что вентильный электропри­вод должен иметь, по крайней мере, две обратных связи: одну – по угло­вой скорости и другую – по току . Это означает также, что электропри­вод должен иметь два за­дающих устройства. Одно задающее устройство с выходным сигналом должно определять требуемый за­кон изменения угловой скорости . Другое задающее устройство должно задавать нулевое значение тока . Это означает, что вырабатываемый этим устройством выходной сигнал должны быть равен нулю. Итак, приходим к выводу, что для выходного сигнала должно выполнятся равенство =0.

Построение структурной схемы вентильного электропривода начнем с построения структурной схемы вентильного двигателя, полагая, что угло­вая скорость , ток и ток являются выходными сигналами, а напряже­ния и – управляющими сигналами. С этой целью преобра­зуем уравнения (3.35) – (3.38) к виду:

, (3.39)

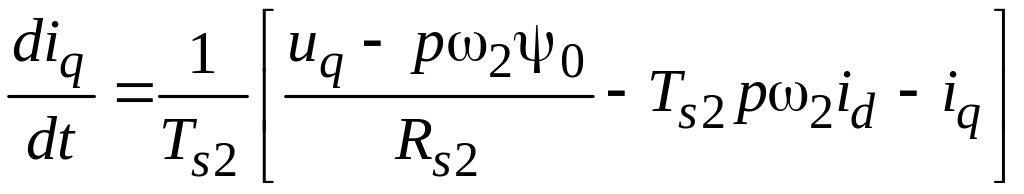, (3.40)

, (3.41)

, где . (3.42)

Уравнениям (3.39) – (3.42), очевидно, соответствует структурная схема вентильного двухфазного двигателя, приведенная на рис.1.

Рис.1. Структурная схема вентильного двухфазного двигателя

в синхронной системе координат

Из этой схемы видно, что на процессы в блоке “Контур регулирования тока ” влияют переменные и . Величина является по сравнению с током весьма инерционной величиной и поэтому не влияет на переходные процессы в контуре регулирования тока . Если обеспечить медленное изменение тока , то ток также не будет влиять на динамику контура регулирования тока . Это означает, что в первом приближении при указанных условиях можно считать контур регулирования тока независимым в динамике от остальной части структурной схемы. Следствием этого свойства является то, что при выборе регулятора тока ( ) можно отбросить возмущающий сигнал (см. рис.1.)

Из структурной схемы вентильного двигателя (см.рис.1) видно также, что если ток =0, то процессы в блоке “Контур регулирования скорости ” не зависят от тока . Это означает, что при выборе регуляторов для контура регулирования скорости можно отбросить возмущающее воздействие .

Приходим, таким образом, к следующему выводу. Для синтеза регуляторов в контуре регулирования тока можно использовать структурную схему, приведенную на рис.2, а для синтеза регуляторов в контуре регулирования скорости можно использовать структурную схему, приведенную на рис.3.

Рис.2. Структурная схема вентильного двигателя для выбора регулятора тока ( )

Рис.3. Структурная схема вентильного двигателя для выбора регулятора угловой скорости (PC) и регулятора тока ( )

При определении передаточной функции регулятора тока ( ) можно воспользоваться любой известной из теории автоматического управления методикой. В частности, можно воспользоваться методикой настройки на технический или симметричный оптимумы при следующих условиях. Во-первых, следует полагать, что быстродействие системы стабилизации тока на нулевом уровне должно быть выше, чем длительность переходных процессов по току и скорости . Во-вторых, следует оценить постоянную времени силового преобразователя, создающего напряжение .

При определении регуляторов системы управления угловой скоростью необходимо обратить внимание на следующее. Структурная схема объекта управления, для которого требуется в этом случае выбирать регуляторы представлена, как это отмечалось выше, на рис.3. Эта структурная схема совпадает, по существу, со структурной схемой двигателя постоянного тока с якорным управлением. Следовательно, здесь могут быть применены все идеи и методики подчиненного управления. Нетрудно видеть, что ток является здесь аналогом якорного тока, а произведение – аналогом противо-ЭДС двигателя постоянного тока. Таким образом, по аналогии с электроприводом постоянного тока с якорным управлением вентильный электропривод должен содержать регулятор скорости (PC) и регулятор тока ( ).

Учитывая изложенное, нетрудно показать, что структурная схема вентильного электропривода в синхронных координатах имеет вид, представленный на рис.4.

Рис.4. Структурная схема вентильного электропривода

с двухфазным двигателем в синхронных координатах

Заметим, что данная структурная схема предназначена, прежде всего для синтеза регуляторов PC, , а также для моделирования процессов в вентильном электроприводе с целью уточнения его динамических свойств после выбора указанных регуляторов.

Для создания реального вентильного электропривода управляющие напряжения и должны быть преобразованы по формулам координатных преобразований в статорные напряжения . Это, во-первых. Во-вторых, для подачи синхронных токов и соответственно на выходы вычитателей токов (см. рис.4) необходимо их получить из реальных статорных токов путем координатных преобразований. С учетом изложенного следует самостоятельно построить функциональную схему вентильного электропривода, включающую схему реального вентильного электродвигателя, схемы координатных преобразователей, датчика положения ротора и силовых преобразовательных устройств.

Выбор регуляторов вентильных электроприводов с трехфазными двигателями может быть произведен аналогично после приведения трехфазного вентильного двигателя к двухфазному. Методика такого приведения аналогична рассмотренной в курсе электрических машин методике приведения асинхронных трехфазных двигателей к двухфазным.

73