36. Закон распределения Пуассона и его характеристики, пример.
ОПР. 7.3. Дискретная случайная величина X имеет закон распределения Пуассона с параметром λ, если она принимает значения 0, 1, 2, …, k, … (бесконечное, но счетное число значений) с вероятностями P(X=k)=(λk/k!)*e-k =Pk(λ).
Если рассмотреть подробнее величину Рn(k), то можно заметить, что в этом выражении есть как бы три переменных: k, n, p. Допустим, что k фиксировано, а n→∞, p→0 притом так, что произведение 𝝀=np есть величина постоянная. При этих предположениях закон распределения Пуассона является предельным случаем биномиального закона и носит название закона редких явлений.
Закон распределения Пуассона выглядит так:
xi |
0 |
1 |
e |
… |
k |
… |
pi |
e-λ |
λ e-λ |
(λ2/2!)* e-λ |
… |
(λk/k!) e-λ |
… |
Определение закона Пуассона задано корректно, так как основное свойство ряда распределения (равенство суммы всех вероятностей единице) выполнено.
Теорема . Математическое ожидание и дисперсия случайной величины X, имеющей закон распределения Пуассона, совпадают и равны λ, т.е. M(X)=D(X)= λ, среднее квадратичное отклонение равно σx=√λ.
Пример. На автоматическую телефонную станцию поступает поток вызовов с вероятностью p=0,8 (вызовов в минуту). Найти вероятность того, что за две минуты (n=2) не придет ни одного вызова.
Решение. Случайная величина X – число вызовов распределена по закону Пуассона с параметром λ=0,8*2=1,6. Тогда P0(λ)=(λ0⁄0!)e-1,6≈0,202.
37. Равномерный закон распределения и его характеристики, пример.
ОПР. Непрерывная
случайная величина X
имеет равномерный закон распределения
на отрезке [a,b],
если ее плотность вероятности постоянна
на этом отрезке и равна нулю вне этого
отрезка, т.е.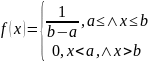
График плотности распределения вероятности непрерывной случайной величины X, имеющей равномерный закон распределения, выглядит так:
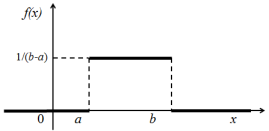
График функции распределения вероятности непрерывной случайной величины X, имеющей равномерный закон распределения, выглядит так:
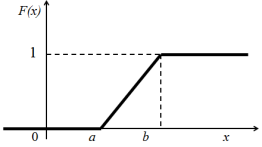
Теорема. Функция
распределения случайной величины X,
имеющей равномерный закон распределения,
имеет вид:
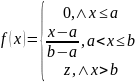
Математическое ожидание случайной величины X, имеющей равномерный закон распределения, равно M(X)=(a+b)/2 ;
Дисперсия случайной величины X, имеющей равномерный закон распределения, равна D(X)=(b-a)2/12 .
Среднее квадратичное отклонение случайной величины X, имеющей равномерный закон распределения, равно σx=(b-a)⁄2√3.
Медиана случайной величины X, имеющей равномерный закон распределения, равна mx=(a+b)⁄2.
Пример. Поезда идут регулярно с интервалом в 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты. Найти мат ожидание и среднее квадратическое отклонение случайной величины Х-времени ожидание поезда.
Решение. Х имеет
равномерное распределение на [0;2].
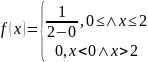
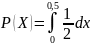=0.25
M(X)=(0+2)/2=1; D(x)=(2-0)2/12=1/3