27 Непрерывные случайные величины. Особенности функции распределения непрерывной случайной величины, примеры.

ОПР. Случайная величина X называется непрерывной, если ее функция распределения является непрерывной в любой точке функцией, а также дифференцируемой всюду, за исключением конечного числа точек.

Теорема . Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю, т.е. P(X=x₁)=0.

Следствие. Если X – непрерывная случайная величина, то вероятность попадания случайной величины в интервал (x₁ , x₂) не зависит от того, является этот интервал открытым или закрытым.

Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле: 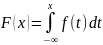функция распределения непрерывной случайной величины – площадь неограниченной слева и справа криволинейной трапеции, но ограниченной сверху кривой распределения, а снизу – осью абсцисс;

Пример. Непрерывная случайная величина имеет плотность вероятности

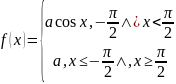
а) Найти коэффициент а; б) построить кривую распределения случайной величины; в) найти вероятность попадания случайной величины в интервал г) найти и построить функцию распределения случайной величины.

Решение. а) Определим коэффициент а из условия

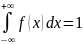
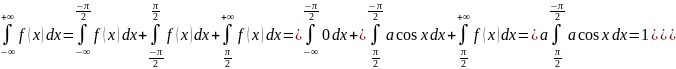
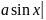_-π/2^π/2=1; 2a=1; a=1/2

б) График кривой распределения имеет вид:

в) Вероятность попадания случайной величины в интервал (0, 𝜋/4) равна

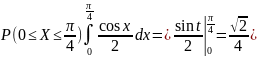
г) Найдем функцию распределения случайной величины

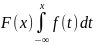
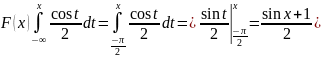
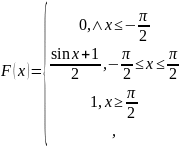
График этой функции имеет вид:

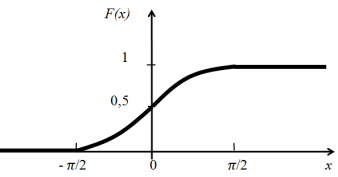
28. Непрерывные случайные величины. Плотность вероятности.

ОПР. Случайная величина X называется непрерывной, если ее функция распределения является непрерывной в любой точке функцией, а также дифференцируемой всюду, за исключением конечного числа точек.

Теорема . Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю, т.е. P(X=x₁)=0.

Следствие. Если X – непрерывная случайная величина, то вероятность попадания случайной величины в интервал (x₁ , x₂) не зависит от того, является этот интервал открытым или закрытым.

Плотность вероятности как производная функции распределения

Рассмотрим вероятность попадания случайной величины на отрезок [x, x+△x]. По формуле P(x₁≤X<x₂)= F(x₂)-F(x₁) эта вероятность равна P(x≤X≤x+△x)=F(x+△x)-F(x), т.е. приращению функции распределения на этом участке. Тогда вероятность, приходящаяся на единицу длины этого участка, по-другому средняя плотность вероятности на участке [x, x+△x] равна

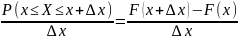
Переходя к пределу при △x⟶0, получим

ОПР. Плотностью вероятности (или плотностью распределения вероятности) f(x) непрерывной случайной величины X называется производная ее функции распределения, т.е. f(x)=F/(x).

Про случайную величину в этом случае говорят, что она распределена с плотностью f(x), а саму плотность вероятности иногда называют дифференциальным законом распределения случайной величины. График плотности вероятности называется кривой распределения.

Основные свойства плотности вероятности

Теорема. Если X – непрерывная случайная величина, а f(x) – ее плотность вероятности, то для нее справедливы следующие свойства:

1. f(x)≥0, т.е. плотность вероятности неотрицательная функция;

2. Вероятность попадания непрерывной случайной величины в интервал [a, b] равен определенному интегралу от ее плотности вероятности в пределах от a до b, т.е.

3. 

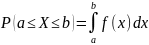
4. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

5. ;

6. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен 1, т.е.

Геометрическое истолкование свойств плотности вероятности таково:

• кривая распределения лежит не ниже оси абсцисс;

• вероятность попадания непрерывной случайной величины в интервал [a, b] – это площадь криволинейной трапеции, ограниченной вертикальными прямыми x=a, x=b, осью абсцисс и кривой распределения;

• функция распределения непрерывной случайной величины – площадь неограниченной слева и справа криволинейной трапеции, но ограниченной сверху кривой распределения, а снизу – осью абсцисс;

• полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.