24. Функция распределения случайной величины, ее свойства.

ОПР. Каждой случайной величине поставим в соответствие некоторую функцию F(x) такую, что при любом значении x₀ она задается равенством F(x₀)=P(X<x₀), т.е. F(x₀) есть вероятность того, что случайная величина X принимает значение, меньшее, чем x₀. Такая функция называется функцией распределения случайной величины X.

Геометрически функция распределения случайной величины X интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки x₀. X<x₀

Приращение функции распределения. Зная функцию распределения F(x), можно найти вероятность любого события вида x₁≤X<x₂. Действительно, для интересующего нас события выполняется неравенство: (X<x₂)=(X<x₁)+ (x₁≤X<x₂). Так как функция распределения, по сути, есть вероятность, то применяя правило сложения вероятностей к последнему неравенству, получим F(x₂)=F(x₁)+P(x₁≤X<x₂). Откуда получаем P(x₁≤X<x₂)= F(x₂)- F(x₁).

По-другому, полученное равенство можно трактовать так: вероятность того, что случайная величина X в результате опыта попадет на участок , равна приращению функции распределения на этом участке.

Вероятность отдельно взятого значения случайной величины

Пусть необходимо посчитать вероятность того, что случайная величина примет значение, равное x₁. Рассмотрим полуинтервал , тогда P(x₁≤X<x₂)= F(x₂)- F(x₁). Станем неограниченно приближать точку x₂ к точке x₁. В пределе получим .

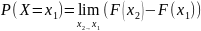Значение этого предела зависит от того, непрерывна функция распределения случайной величины в точке x₁ или нет. Если функция распределения случайной величины в точке x₁ непрерывна, то полученный предел равен нулю, т.е. вероятность того, что случайная величина примет значение, равное x₁, будет равна нулю. Если же в этой точке функция распределения терпит разрыв первого рода, т.е. имеет скачок, то этот предел будет равен величине скачка.

Свойства функции распределения

Теорема .Справедливы следующие свойства функции распределения случайной величины:

1. Функция распределения F(x) является неубывающей, т.е. если x₂>x₁, то F(x₂)≥F(x₁).

2. Справедливы равенства ,

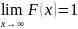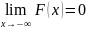
3. Функция F(x) является непрерывной слева при любом x, причем F(x-0)=F(x). Это означает, что, если случайная величина X стремится к точке x слева, то значение функции распределения при таком стремлении совпадает со значением в самой точке x.

4. Вероятность события равна величине скачка функции распределения случайной величины X в точке x₁ (равен этот скачок нулю или нет).

Характеристический признак функции распределения

Существуют ли характеристические свойства, по которым можно судить, что данная функция является функцией распределения некоторой случайной величины?

Теорема. Пусть дана функция F(x), определенная для всех значений x и обладающая свойствами:

1. F(x) не убывает;

2. , .

3. Функция F(x) является непрерывной слева при любом x.

Тогда существует, причем единственная, случайная величина X, функция распределения которой есть F(x).