МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛЖСКИЙ ПОЛИТЕХНЧЕСКИЙ ИНСТИТУТ (филиал)

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

КАФЕДРА “ТЕХНОЛОГИЯ И ОБОРУДОВАНИЕ МАШИНОСТРОИТЕЛЬНЫХ ПРОИЗВОДСТВ”

ПРАКТИКУМ ПО ОПРЕДЕЛЕНИЮ КЛАССА ТОЧНОСТИ ОТЛИВОК

Методические указания к выполнению ОргСРС по дисциплинам «Технологические процессы в машиностроении» и «Технология конструкционных материалов»

РПК “Политехник”

Волгоград

2009

УДК 620.19

ПРАКТИКУМ ПО ОПРЕДЕЛНИЮ КЛАССА ТОЧНОСТИ ОТЛИВОК:

Методические указания к выполнению ОргСРС по дисциплинам «Технологические процессы в машиностроении», «Технология конструкционных материалов» / Сост. Т.С. Тарасова, Е.Ф. Уткин; Волгоград, гос. техн. ун.-т – Волгоград, 2009, 28 с

Излагается краткая теория о причинах, влияющих на точность отливок.

Показана оценка точности выпускаемых отливок на основе использования методов статистического анализа. Рассматривается пример определения класса точности отливки, приводится справочный материал и варианты заданий.

Предназначены в помощь студентам, обучающимся по направлению 551800

«Технологические машины и оборудование» и 552900 «Технология, оборудование и автоматизация машиностроительных производств» при выполнении ОргСРС.

Ил.: 5 Табл.: 7 Библиограф.: 4 назв.

Рецензент: О.А. Тишин

Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета

©Волгоградский

Государственный

Технический

Университет, 2009

1. Цель работы

Изучение проблемы качества отливок определяемой классом точности, обеспечиваемым данным технологическим процессом. Ознакомление с методикой проведения статистического анализа операции. Установление закона распределения размеров отливок и расположения поля рассеяния размеров.

2. Теоретическая часть

Разрабатывая технологию изготовления отливки необходимо решить главную задачу: изготовить изделие в заданном количестве и требуемого качества при минимальных затратах труда, материалов, энергии и минимального воздействия на окружающую среду.

Среди требований, предъявляемых к качеству продукции, особое внимание уделяется размерной точности отливок. Это объясняется следующими причинами:

1. Потерями металла от низкой размерной и весовой точности отливок и увеличенных припусков на механическую обработку.

2. Использованием технологической оснастки, рассчитанной на жесткий допуск размеров, обрабатываемых отливок, устанавливаемой на современном автоматическом металлообрабатывающем оборудовании (станки с ЧПУ).

3. Непосредственной зависимостью надежности, долговечности и работоспособности машин и механизмов, от точности изготовления, как самого изделия, так и отдельных его частей, следовательно, и литых деталей.

4. Стоимостью отливок определяемой их качеством, в том числе и точностью.

Исходя из вышеизложенного, необходимо знать, какой класс точности отливок обеспечивается данным технологическим процессом.

Класс точности отливки оговаривается в чертеже или в технических условиях, однако необходимо периодически экспериментально оценивать реальный класс точности выпускаемых отливок по мере износа литейной оснастки и изменений в технологическом процессе. Такая оценка проводится с использованием методов статистического анализа, так как изготовление сопровождается явлениями случайного характера.

Распределение случайных величии в зависимости от условий могут подчиняться вполне определенным законам. Наибольшее практическое значение в технологии машиностроения имеет закон нормального распределения или закон Гаусса, для которого плотность вероятности или дифференциальная функция распределения:

где x – переменная случайная величина;

- среднее квадратическое отклонение величины x от m_х;

- математическое ожидание величины x (центр группирования);

В практических задачах положение центра группирования характеризует среднее арифметическое значение случайной величины :

где - частота определенных значений ;

- число отдельных значений ;

n - общее число значений ;

Среднее квадратическое отклонение для практических распределений:

.

Таким образом, для того чтобы охарактеризовать распределение случайной величины, надо иметь как минимум две числовые характеристики. Одна из них ( или ) определяет положение центра группирования, другая разброс значений случайной величины около центра группирования.

Характеристиками распределения считают поле рассеяния случайной величины:

и координаты середины поля рассеяния:

В симметричных распределениях центр группирования оказывается совмещенным с .

Дифференциальная функция закона нормального распределения графически изображается холмообразной кривой, симметричной относительно центра группирования, представляемого величинами или ( ) (рис 1). Координата центра группирования определяет положение кривой относительно начала отсчета, а параметр - ее форму и размах.

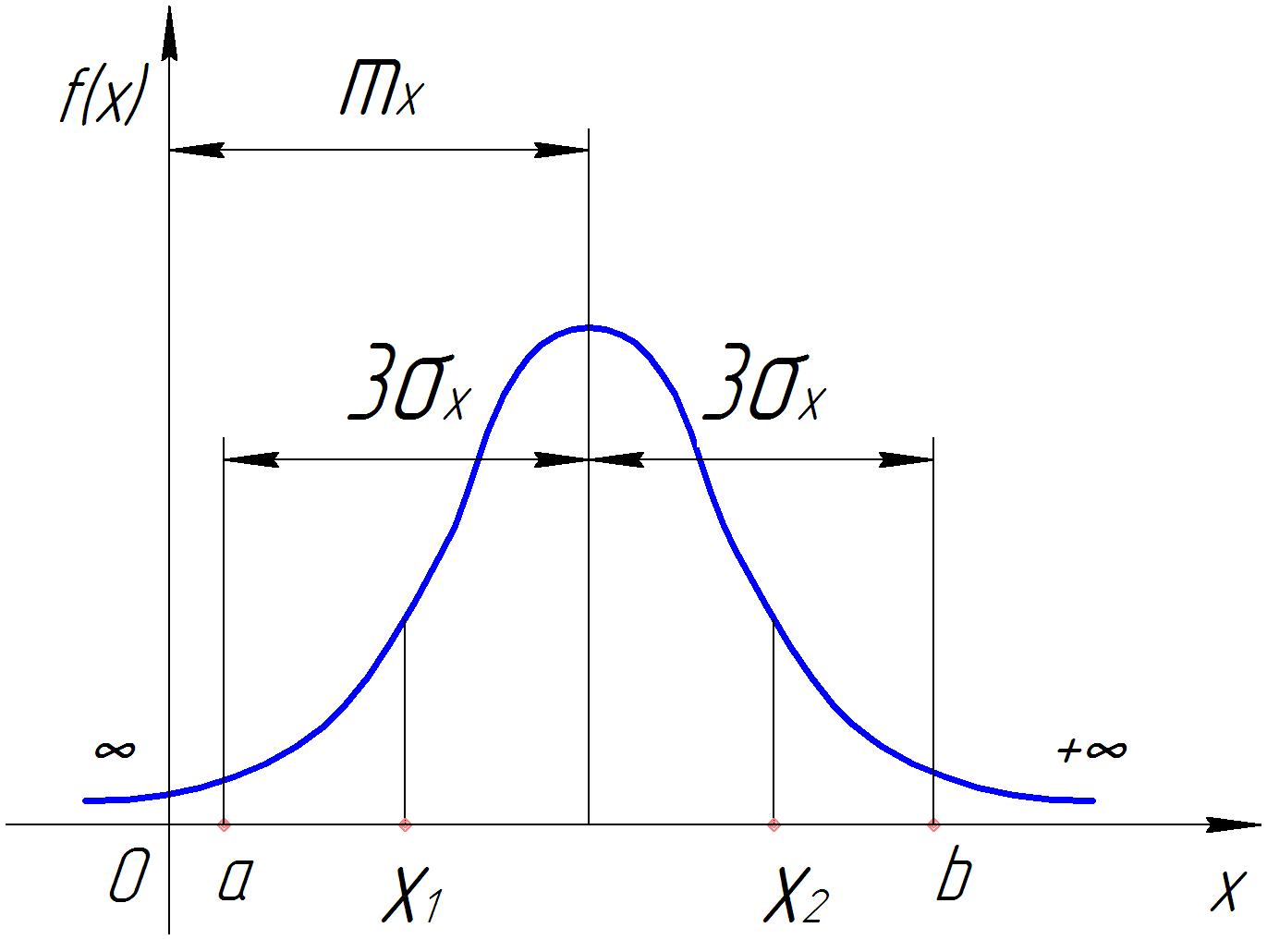
Рис 1. Дифференциальный закон нормального распределения случайной величины.

Функцию или интегральный закон нормального распределения в общем виде можно записать так:

Если изменение случайной величины x следует закону нормального распределения, она может принимать любые значения в пределах .

Поэтому:

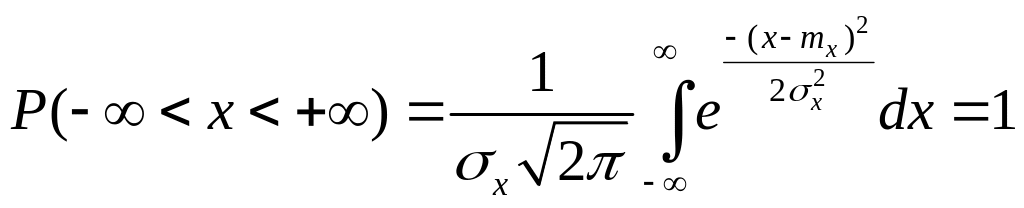
Вероятность =1 представляет собой площадь под дифференциальной кривой закона нормального распределения. Очевидно, что вероятность значений x в любом другом интервале меньше единицы:

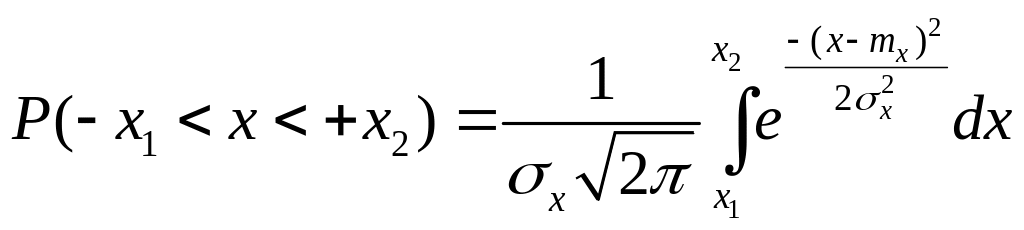
Для облегчения вычисления эту формулу, с помощью нормирующего множителя , можно привести к виду:

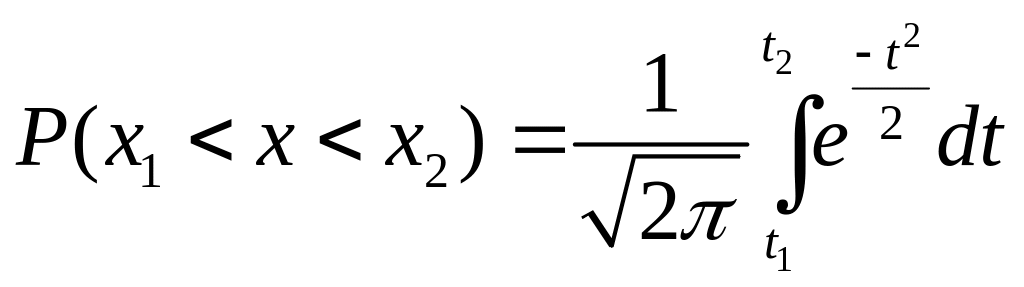
Интеграл называют нормированной функцией Лапласа и его значение для различных приводятся в таблицах, именуемых «Значения функции Лапласа». При использовании таблиц решение задачи по определению вероятности того, что случайная величина x находится в пределах , сводится к нахождению разности между двумя значениям функции Лапласа:

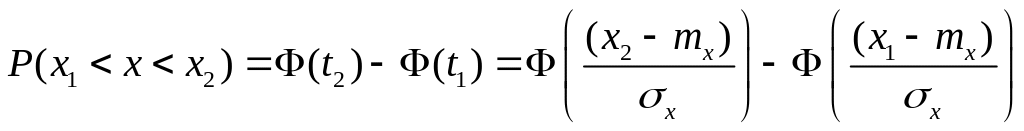
Считают, что практическая зона рассеяния случайной величины x, подчиняющейся закону нормального распределения, лежит в пределах и составляет . При и значения

и

Следовательно:

.

Согласно таблицам, содержащим значения функции Лапласа, . Это означает, что вероятность нахождения случайной величины вне указанного интервала q=1 - P = 1 - 0.9973 = 0.0027, то есть очень мала.

Ограничение величины рассеяния 6 объясняется объективными экономическими причинами, обусловленными уровнем развития науки и техники. В ряде случаев используют и более широкие пределы, например .

Распределение случайной величины по нормальному закону является следствием действия многих факторов, носящих случайных характер, имеющих примерно одинаковую степень активности и независящих или слабо зависящих один от другого. Такой комплекс условий не всегда оказывается полным. Его нарушение, даже в какой- то степени, приводят к отклонению закона распределения от нормального.

Одной из форм таких отклонений может быть несимметричность кривой рассеяния (рис. 2), характеризуемая коэффициентом асимметрии , учитывающим смещение центра группирования относительно координаты середины поля ­­­­рассеяния :

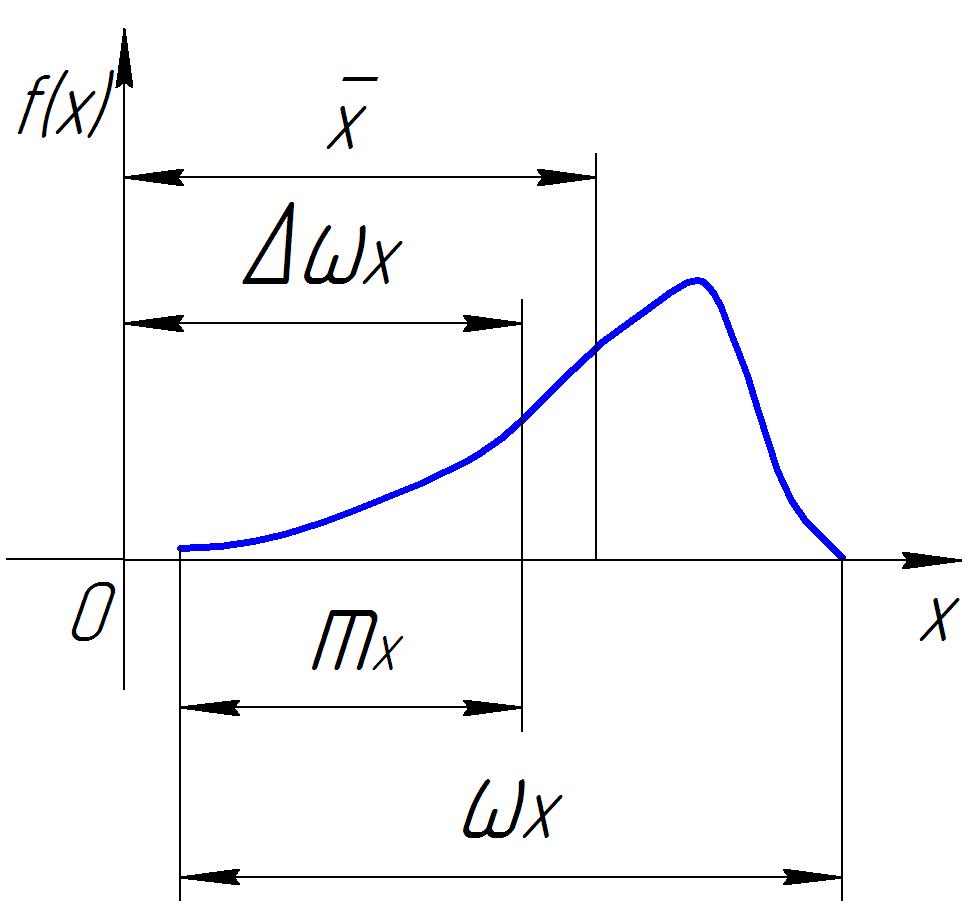
Рис. 2 Несимметричное распределение случайной величины

Условия решения задачи могут иметь различную специфику. В соответствии с этим распределения случайных величин могут быть подчинены другим законам.

Распределение по закону равной вероятности встречаются, когда наряду со случайными факторами, вызывающими рассеяние, действует доминирующий систематический фактор, непрерывно и равномерно изменяющий во времени положение центра группирования . Графически такое распределение случайной величины отображается прямоугольником (рис. 3):

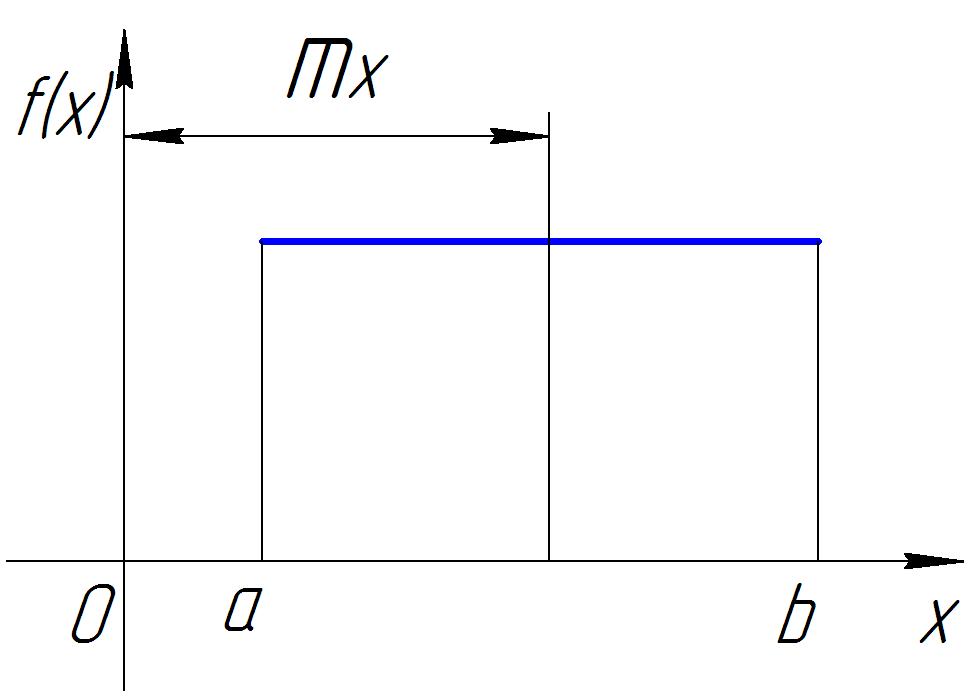
Рис. 3. Распределение случайной величины по закону равной вероятности.

При изменении случайной величины x в интервале от a до b

Дифференциальный закон распределения или плотность вероятности

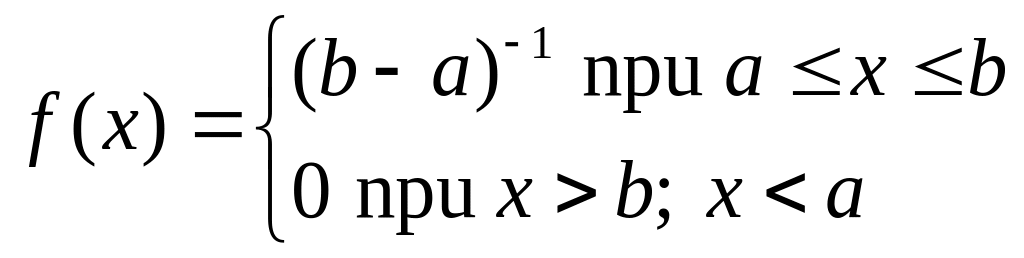
Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:

.

Распределение по закону Симпсона происходит при сложении двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равностороннего треугольника (рис 4.), из-за чего закон Симпсона часто называют законом треугольника.

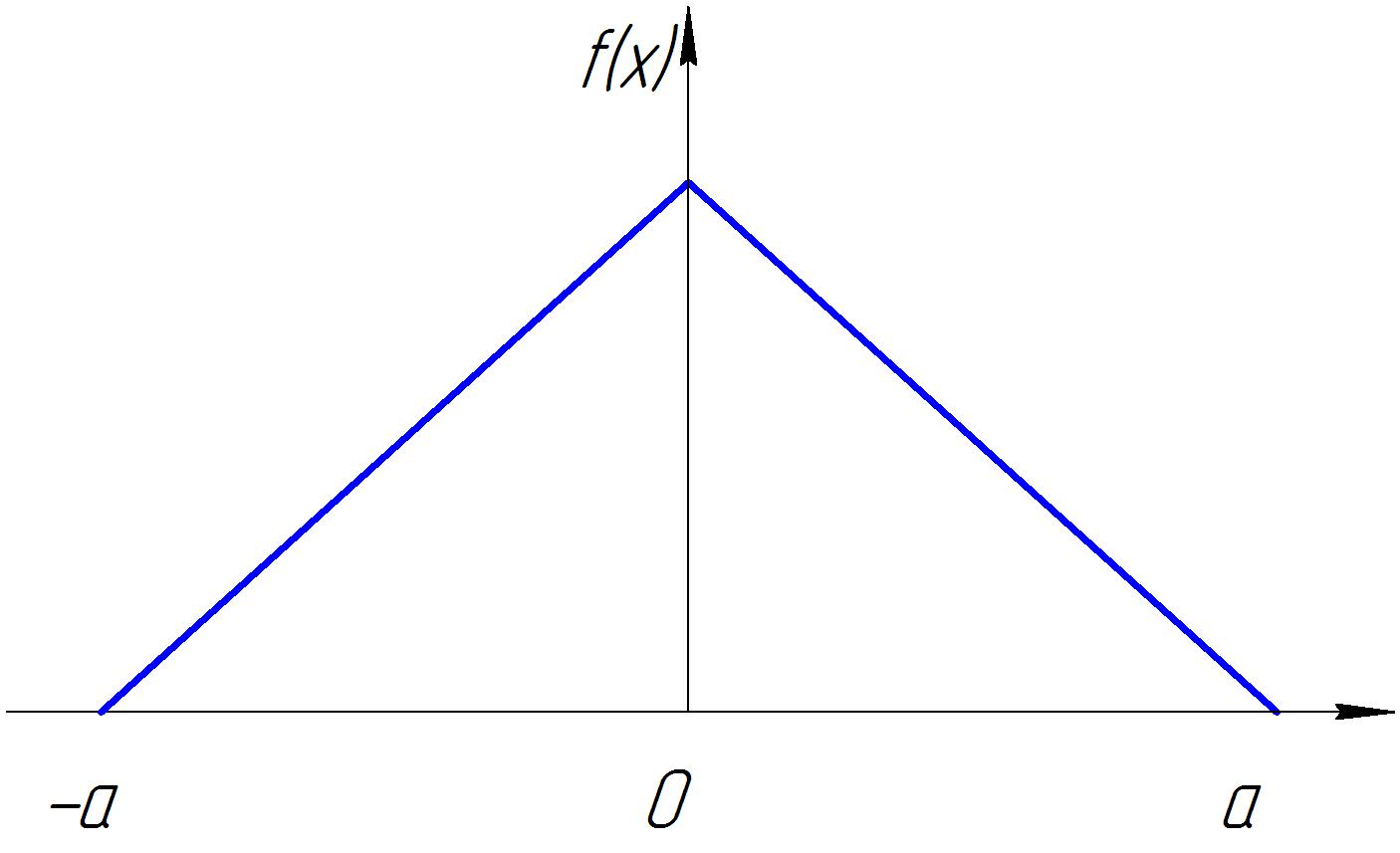
Рис. 4. Распределение случайной величины по закону Симпсона

При выборе в качестве начала отчета случайно величины, ее математическое ожидание, характеристики распределения имеют следующий вид:

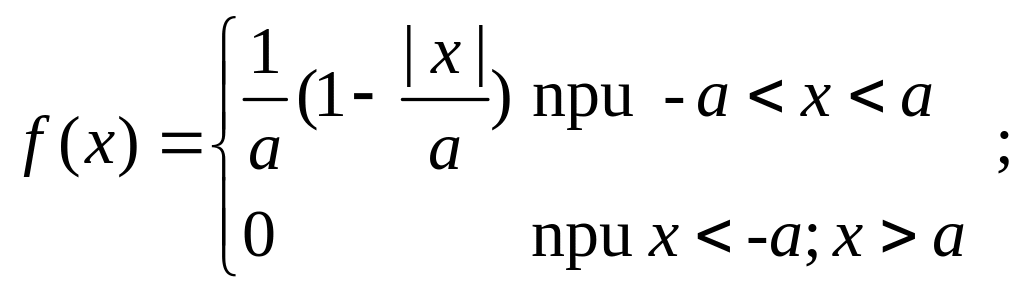
Если распределения по закону Симпсона и равной вероятности рассматривать как отклонения от закона нормального распределения, то можно отразить и количественную сторону этих отклонений с помощью коэффициента , именуемого средним квадратическим отклонением:

Подставив в эту формулу величины и , соответствующие трем законам распределения случайной величины, получим для каждого из них свое значение коэффициента (табл. 1):

Таблица 1.

Закон распределения
Нормальный (Гаусса)		6
Симпсона		2а
Равной вероятности		b-a