
- •Ток и напряжение в электрических цепях
- •Линейные электрические цепи при постоянных токах
- •Основные пассивные элементы электрических цепей
- •Активные элементы электрических цепей
- •Баланс мощностей в цепях постоянного и переменного тока
- •6. Закон Ома для участка цепи с электродвижущей силой
- •7.Обобщенный закон Ома
- •11.Метод контурных токов
- •12.Метод наложения (теорема суперпозиции)
- •13. Теорема Тевенина.
- •14. Теорема Нортона
- •13. Биполярные транзисторы
- •14. Полупроводниковые диоды
- •15. Выпрямительные электронные устройства
- •Усилительные устройства
- •17.Типы усилителей на транзисторах
- •18.Понятие о гармонических функциях напряжения и тока
- •19.Метод комплексных амплитуд
- •20.Характеристики пассивных элементов электрической цепи в гармоническом режиме (конденсатор)
- •21.Частотные характеристики пассивных линейных двухполюсников
- •22.Частные характеристики колебательных контуров
- •23.Резонанс токов.
- •24.Мгновенная и активная мощности
- •25. Реактивная, полная и комплексная мощности
- •27.Энергетические процессы в цепях гармонического тока
- •28. Индуктивно-связанные цепи
- •29.Понятие о линейных четырехполюсниках
- •30.Общие сведения о трехфазных цепях
- •31. Подключение трехфазного генератора к цепи потребителя звезда-звезда
- •32. Подключение трехфазного генератора к цепи потребителя треугольник- треугольник
- •33. Симметричный режим работы трехфазной цепи
- •34. Трехфазные цепи при несимметричных нагрузках
- •Измерительные трансформаторы
- •Режимы работы трансформаторов
- •Автотрансформатор
- •Устройство и принцип работы трансформатора.
- •Способы возбуждения генераторов постоянного тока
- •41. Устройство и принцип работы генератора постоянного тока
- •42. Эдс и вращающий момент генератора постоянного тока
- •4 3.Электрические машины постоянного тока
- •44.Двигатели с параллельным и независимым возбуждением
- •Способы возбуждения двигателей постоянного тока
- •46. Двигатели постоянного тока
- •Однофазный асинхронный двигатель
- •Устройство и принцип работы асинхронного двигателя
- •Асинхронный двигатель с фазным ротором
- •Рабочие характеристики асинхронного двигателя
- •Асинхронные электрические машины
- •52.Классификация машин переменного тока
- •53. Характеристики синхронного двигателя
- •54.Характеристики синхронного генератора
- •55. Регулировочная характеристика
- •56. Работа синхронной машины в режиме двигателя
- •57. Устройство и принцип работы синхронного генератора
- •58. Основные режимы работы электропривода
- •59. Уравнение движения электропривода
11.Метод контурных токов
В методе контурных токов количество уравнений задачи анализа сводится к числу независимых уравнений, которые требуется составлять по второму закону Кирхгофа. Число таких уравнений: p – (q – 1) – k. При использовании метода контурных токов задачу начинают решать с выбора достаточного количества независимых контуров и задания в каждом контуре новой функции – контурного тока, циркулирующего по контуру в определенном (условном положительном) направлении. Уравнение для каждого контура составляют по второму закону Кирхгофа суммированием при обходе по контуру напряжений на ветвях, входящих в его состав. Если ветвь оказывается общей для нескольких контуров, ток, текущий по ней, складывается из контурных токов, замыкающихся через эту ветвь. Если в цепи имеются источники токов, с ними поступают особым образом. Ветвь, содержащую источник тока, включают только в один контур. Контурный ток для него принимают равным току источника и уравнение для этого контура не составляют.
Для цепей с сопротивлениями в общем случае контурные токи будут удовлетворять следующей системе уравнений:
……………………………
|
|
Метод основан на ЗНК и позволяет сократить число совместно решаемых уравнений с Nв до Nв – (Nу – 1) .
Последовательность расчета:
а) выбираем положительные направления токов в ветвях;
б) выбираем независимые контуры и обозначаем их контурные токи; количество независимых контуров равно К = Nв – (Nу – 1);
в) составляем систему алгебраических уравнений для контурных токов:
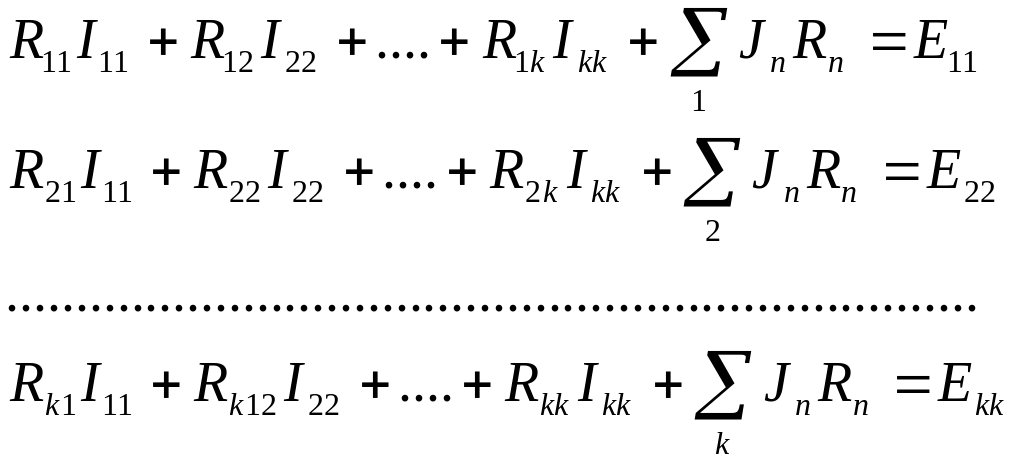
Здесь I11, I22,..,Iкк – контурные токи первого, второго и К-го контуров; ∑ Jn Rn - алгебраическая сумма произведений тока Jn, источника тока n-й обобщенной ветви, смежной с контуром m, на её сопротивление Rn; при этом со знаком плюс (минус) берутся те произведения, ток Jn которых совпадает (противоположен) с направлением контурного тока Inm. Правые части уравнений представляют собой контурные ЭДС, равные алгебраической сумме ЭДС, действующих в рассматриваемом контуре, при этом с положительным (отрицательным) знаком берутся те ЭДС, положительные направления которых совпадают (противоположны) с произвольно выбранным направлением обхода данного контура
г) после определения контурных токов находим действительные токи в ветвях схемы, при этом необходимо учитывать положительные направления контурных токов и выбранные в начале положительные направления токов в ветвях схемы.
12.Метод наложения (теорема суперпозиции)
В тех случаях, когда в линейной
ЭЦ действует два или более источника
электрической энергии, результирующая
реакция (ток и напряжение) может быть
получена как сумма отдельных реакций
(наложение) от поочередного действия
каждого отдельно взятого источника в
то время как действия других источников
равны нулю, а они сами заменены их
внутренними сопротивлениями. Источник
ЭДС, который мы считаем равным нулю
![]() ,
при равенстве нулю его внутреннее
сопротивление эквивалентно замещению
его закороченной ветвью. Источник тока,
который мы считаем равным нулю, означает
,
при равенстве нулю его внутреннее
сопротивление эквивалентно замещению
его закороченной ветвью. Источник тока,
который мы считаем равным нулю, означает
![]() ,
что эквивалентно замещению источника
тока разомкнутой ветвью.
,
что эквивалентно замещению источника
тока разомкнутой ветвью.
ПРАВИЛО ЗНАКОВ. Реакции цепи, совпадающие по направлению с результирующей реакцией, берутся со знаком плюс, в противном случае – со знаком минус.
Метод наложения может применяться для обоснования других методов анализа, в частности метода компенсации и когда в схеме с несколькими источниками изменяются параметры одного из них.
Пример. В
ЭЦ (рис. 4.1) рассчитать напряжение
![]() методом наложения.
методом наложения.

Рис.4.1
В этом и последующих решениях
будем использовать схему, в которой
источник тока заменен на эквивалентный
источник напряжения с ЭДС
![]() .
.
Так как в цепи имеется
![]() источника питания, то решение задачи
посредством метода наложения будет
проходить в четыре этапа. В каждом из
них мы зануляем все источники питания
кроме одного и производим расчет токов
на каждом элементе.
источника питания, то решение задачи
посредством метода наложения будет
проходить в четыре этапа. В каждом из
них мы зануляем все источники питания
кроме одного и производим расчет токов
на каждом элементе.
1)
![]() - задано,
- задано,
![]() .
.
Для расчета данной схемы необходимо
преобразовать 3-х лучевую звезду
![]() ,
,
![]() ,
,
![]() в треугольник
в треугольник
![]() ,
,
![]() ,
,
![]() причем,
причем,
|
|
и
![]() ,
а также
и
,
а также
и
![]() попарно параллельны и последовательно
соединены друг с другом, т.е.
попарно параллельны и последовательно
соединены друг с другом, т.е.
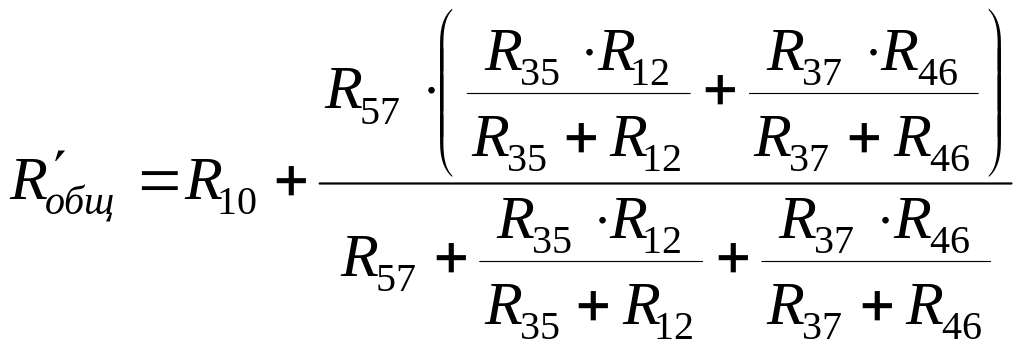 ;
;
Теперь найдем
![]() .
Ток, протекающий через параллельные
ветви (
.
Ток, протекающий через параллельные
ветви (![]() ,
,
![]() ).
).
![]() ,
,
![]() ,
,
![]() .
.
Остальные токи найдем через применение ЗТК:
![]() ,
,
![]() ,
,
![]() .
.
2)
![]() - задано
- задано
![]()
Преобразуем трехлучевую звезду сопротивлений , , в треугольник сопротивлений:
|
|
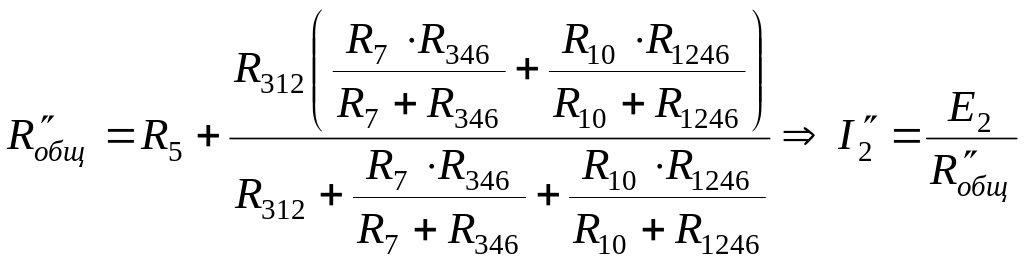 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3)
![]() - задано,
- задано,
![]()
Звезду , , преобразуем в треугольник , , (значения сопротивлений известны из 1-го шага)
|
|
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4)
![]() ,
,
![]()
Преобразуем звезду
,
![]() ,
в треугольник, где
,
в треугольник, где
![]() ,
,
![]() ,
,
![]() :
:
|
|
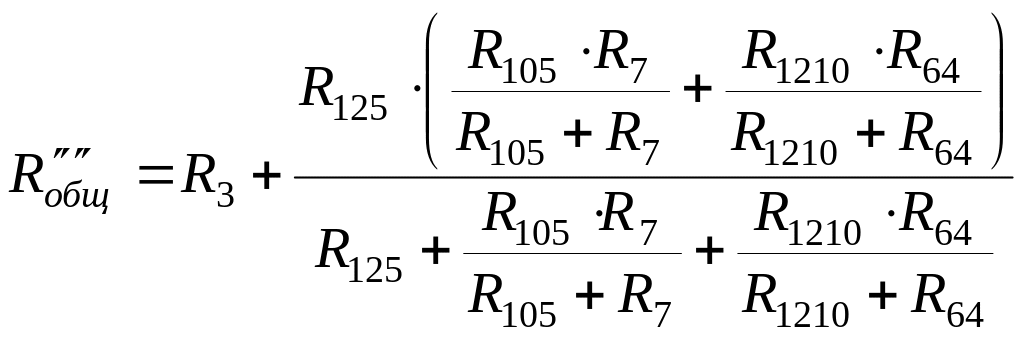 ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() Тогда
токи на элементах:
Тогда
токи на элементах:
![]() .
.




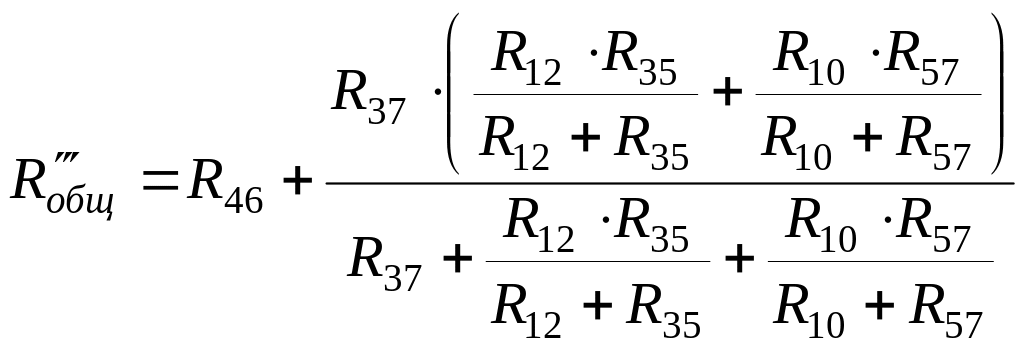 ,
,
