5. Баланс мощностей в цепях постоянного и переменного тока

На основании закона сохранения энергии можно записать баланс мощности для цепей постоянного тока: для любой замкнутой электрической цепи содержащей n-контуров (n=1,2…), сумма мощностей P_И развиваемых источниками электрической энергии, равна сумме мощностей P_П расходуемых в приёмниках энергии:

или ,

где - энергия в единицу времени (мощность), доставляемая в цепь источниками электродвижущей силы. Слагаемые , в которых положительные направления электродвижущей силы и соответствующего тока совпадают, берем со знаком плюс. В противном случае со знаком минус. -алгебраическая сумма, доставляемой источниками тока мощности в электрическую цепь. Здесь положительны те слагаемые, у которых напряжение на источнике тока U_в и его ток J_в совпадают по направлению. В противном случае слагаемое отрицательно.

-арифметическая сумма мощностей, рассеиваемых на сопротивлениях электрической цепи.

1. Проверка баланса мощностейсостоит в выполнении равенства:

6. Закон Ома для участка цепи с электродвижущей силой

Для однозначного определения потенциала любой точки электрической цепи необходимо произвольно принять потенциал какой-нибудь одной точки за опорный. Так для изображенных участков цепи выразим потенциал точки а через потенциал точки с.

При перемещении от точки c к точки b:

встречно направлению источника согласно с направлением источника

φ_в= φ_с-Е φ_в= φ_с+Е

Ток течёт от более высокого потенциала к более низкому. Поэтому φ_а выше φ_в на величину падения напряжения на сопротивлении R:

φ_а= φ_в+IR

φ_а= φ_с-Е+IR φ_а= φ_с+Е+IR

U_аc= φ_a- φ_c= IR-Е (3) U_аc= φ_a- φ_c= Е+IR

U_ca= φ_c- φ_a= Е-IR U_ca= φ_c- φ_a= -Е-IR

φ_c= φ_a-IR+E φ_c= φ_a-E-IR

, (4)

где R_ав -суммарное сопротивление участка цепи.

φ_а- φ_в= U_ав- напряжение между зажимами рассматриваемого участка, взятое по выбранному направлению тока. -алгебраическая сумма источников электродвижущей силы на том же участке, причём каждый источник совпадающий по направлению с направлением тока, записывается с знаком, а не совпадающий с .

Формула (4) представляет собой закон Ома для участка цепи с источником электродвижущей силы.

7.Обобщенный закон Ома

При анализе сложных электрических схем, содержащих источники электродвижущей силы и тока, удобно использовать понятие обобщенной ветви. Обобщенная ветвь содержит сопротивление R_в, идеальный источник электродвижущей силы. U_в идеальный источник тока J_в (рис.12)

Ток, текущий через сопротивление R_в:

По ЗТК

Н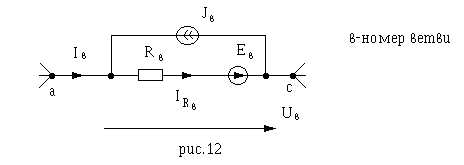 апряжение обобщенной ветви:

Ток обобщенной ветви:

(5)

Формула (5) представляет собой закон Ома для обобщенной ветви.

8.Метод непосредственного использования законов Кирхгофа

Для конкретной цепи можно составить уравнения по первому и второму законам Кирхгофа для всех узлов, имеющихся в цепи, и всевозможных контуров, которые можно указать на схеме. Пусть схема построена из двухполюсных элементов без взаимных индуктивностей и содержит р ветвей, q узлов и k источников тока. По первому закону Кирхгофа достаточно составить q – 1 уравнение. Необходимое число уравне­ний, удовлетворяющих второму закону Кирхгофа: р – (q – 1) – – k. Если источники тока в цепи отсутствуют, тогда число независи­мых уравнений, которые получаются на основании первого и второго законов Кирхгофа, совпадает с числом ветвей в схеме.

При составлении уравнений по второму закону Кирхгофа нужно так выбирать совокупность контуров, чтобы уравнения оказались независимыми. Тогда и кон­туры из этой совокупности называют независимыми. Всего их должно быть: р – (q – 1) – k. В каждом таком контуре должна оказаться какая-либо ветвь, не со­держащаяся в каком-нибудь другом контуре. Существуют разные способы фор­мирования набора независимых контуров. При решении задачи анализа составляют по законам Кирхгофа требуемое число независимых уравнений для узлов и контуров электрической цепи. Для каждой ветви записывают компонентные соотношения, связывающие токи и на­пряжения на элементах, составляющих ветвь. В результате должно получиться столько уравнений, сколько требуется для отыскания неизвестных напряжений и токов.

Методика составления уравнений по ЗТК:

1. Произвольно выбираем положительное направление токов в ветвях и обозначим их.

2. Записываем (n_у- 1) линейно-независимых уравнений.

Токи втекающие в узел будем считать отрицательными(-); вытекающие из узла – положительными(+).

Методика составления уравнений по ЗНК:

1. Произвольно выбираем положительное направление обхода контура.

2. При записи левой части (1) со знаком (+) - если падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с положительным направлением обхода контура (независимо от направления электродвижущей силы в этих ветвях), со знаком (-) - если положительное направление тока противоположно направлению обхода. При составлении уравнений по ЗНК следует выбирать независимые контуры (т.е. контуры, которые содержать хотя бы одну ветвь, не входящую в другие контуры) не содержащие источников тока.

3. Если направления электродвижущей силы совпадают с выбранным положительным направлением обхода контура (независимо от направления тока, протекающего через них), то они принимаются положительными. Электродвижущие силы направленные против выбранного направления обхода - принимаются отрицательными (правая часть(1)).

4. Составляем число уравнений равное числу ветвей без источников тока (n_в- n_в.и.т) минус число уравнений составленных по ЗТК, т.е. (n_в- n_в.и.т)- (n_у- 1)= n_в- n_в.и.т-n_у+1.

Таким образом, составляя уравнения, следует охватить все ветви схемы исключая ветви с источниками тока.

9.Методы эквивалентного преобразования схем

Преобразование считается эквивалентным, если оно не изменяет токи и напряжения в непреобразованной части цепи. При этом изменение топологии ЭЦ не меняет её свойств..

1. Л юбой источник тока может быть заменен эквивалентным источником напряжения и наоборот. При этом источник тока, эквивалентный источнику напряжения, должен генерировать ток, равный току короткого замыкания источника напряжения, и иметь параллельное внутреннее сопротивление, равное последовательному внутреннему сопротивлению источника напряжения, т.е. схемы эквивалентны, если

или

2. Последовательное соединение резисторов при эквивалентной замене суммируется:

,

где – число последовательно соединенных резисторов. При данном соединении всегда больше большего из сопротивлений. В частном случае, если каждое из сопротивлений равно , то .

3. При параллельном соединении резистора суммируется их проводимость , и . При параллельном соединении всегда меньше меньшего из сопротивлений. В частном случае, если каждое из сопротивлений равно , то . В случае двух параллельно соединенных сопротивлений и :

	=
	или	.

4. При смешанном соединении резисторов эквивалентное сопротивление цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному . При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.

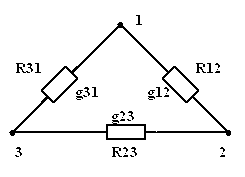
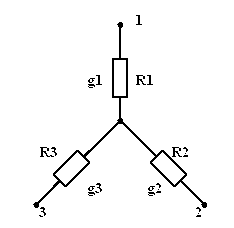
5. Преобразование пассивного треугольника сопротивлений в эквивалентную трехлучевую звезду. Схемы будут эквивалентны, если сопротивления между узлами и , и , и в обеих схемах «звезды» и «треугольника» будут одинаковыми:

=

, , .

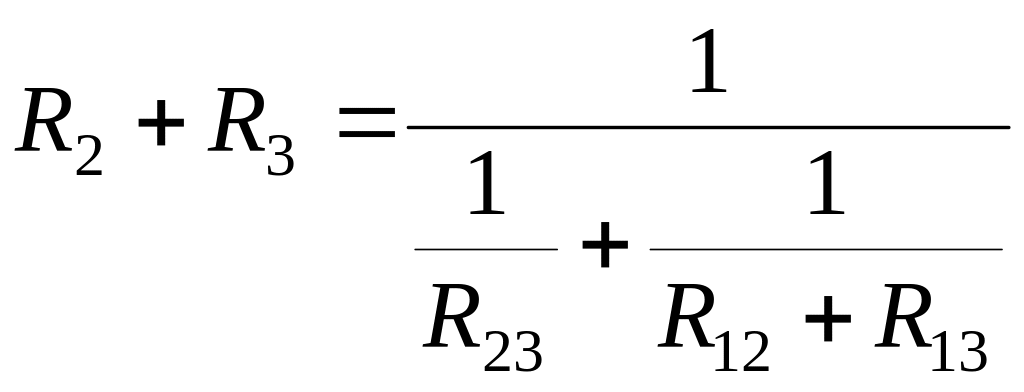
Решая совместно эти уравнения, получим:

, , ,

, , .

Обратное преобразование трехлучевой звезды в треугольник:

, , .

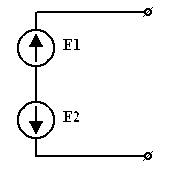
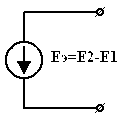
6. Преобразование ветвей, содержащих последовательные и параллельные соединения источников ЭДС и тока.

			=
	=				или

7

а)

д)

. Часть схемы, состоящей из параллельных ветвей ЭДС и проводимостями , эквивалентно либо одной ветви с проводимостью и ЭДС :

, ,

либо двум параллельным ветвям с той же проводимостью и источником тока :

.

10.Метод узловых потенциалов

При методе узловых потенциалов вычисляют потенциалы узлов. Пусть в схеме имеется q узлов. Одному из узлов схе­мы присваивают нулевое значение, и такой узел становится опорным, или базисным. Потенциалы остальных узлов схемы отсчитывают по отношению к опорному узлу. Ток в каждой ветви схемы можно выразить через разность узловых потенциалов. Согласно пер­вому закону Кирхгофа приравнивают нулю сумму токов ветвей, сходящих в узел, и получают систему независимых уравнений. Их количество (q – 1) совпадает с ко­личеством неизвестных функций – узловых потенциалов. Уравнения решают и по найденным потенциалам узлов вычисляют напряжения на ветвях (как разность потенциалов) и токи в ветвях. Если между двумя узлами включен источник ЭДС е, тогда один узел этой пары резонно выбрать в качестве опорного. Очевидно, что потенциал другого узла будет известен – он равен е.

Если в схеме имеются источники напряжения – источники ЭДС e_k с подключенными последовательно сопротивлениями R_ke, – их заменяют эквивалентными источниками тока i_k = e_k/R_k, к которым параллельно подключе­ны проводимости G_ke = 1/R_ke. Далее вводят узловые потенциалы, подлежащие на­хождению, и составляют уравнения по первому закону Кирхгофа для токов в уз­лах в достаточном для данной задачи количестве.

Если обозначить общее число независимых уравнений буквой m, систему уравне­ний, построенную по методу узловых потенциалов, можно записать в виде:

МУП является дальнейшим развитием метода уравнений Кирхгофа и позволяет сократить число совместно решаемых уравнений до N_у – 1.

Последовательность расчета:

а) выбираем положительные направления токов в ветвях;

б) выбираем опорный узел, потенциал которого считаем равным нулю;

в) для оставшихся N_у – 1 узлов составляем уравнения:

Здесь – узловая проводимость, равная арифметической сумме проводимостей ветвей, присоединенных к узлу i; всегда больше нуля; - алгебраическая сумма произведений ЭДС ветвей, присоединенных к узлу s, на проводимости этих ветвей: при этом со знаком плюс (минус) берутся те ЭДС, которые направлены к узлу (от узла); - алгебраическая сумма токов источников тока ветвей, присоединенных к узлу s; при этом со знаком плюс берутся токи, направленные к узлу s.

г) по найденным потенциалам узлов определяем токи в ветвях,