23.Резонанс токов.

Параллельным колебательным контуром называется электрическая цепь, в которой L и C размещены в двух ветвях, подключенных параллельных источнику энергии. На резонансной частоте мнимая составляющая входной проводимости параллельной RLC-цепи должно быть равно 0: ,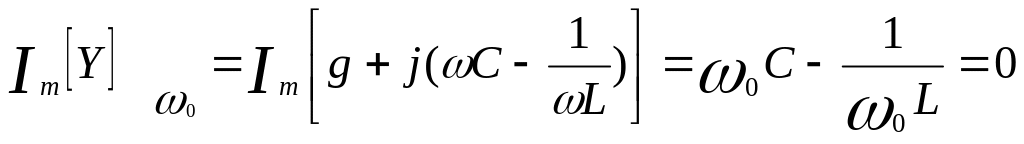

из этого следует, что

Векторная диаграмма для случая резонанса:

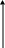
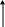
0

При противоположные по фазе реактивные составляющие токов равны. Поэтому резонанс в рассматриваемой цепи называется резонансом токов.

При действующие значения токов ветвей контура:

Входной ток контура равен току проводимости g:

Отношение действительного значения тока реактивного элемента к входному току параллельного колебательного контура на называется добротностью параллельного колебательного контура:

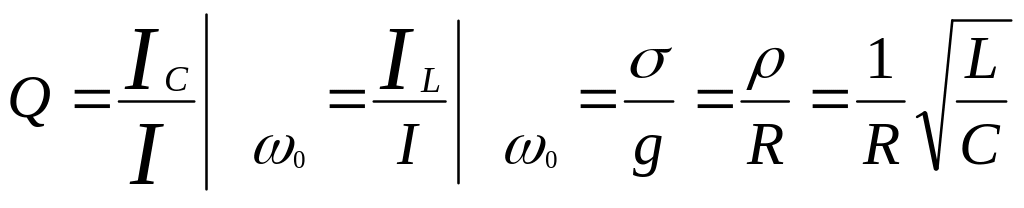
Из чего следует, что с увеличением проводимости потерь g, уменьшается Q, т.о. Q параллельного контура совпадает с Q последовательного контура.

Резонанс напряжения

Резонансом называется такое явление в цепи, содержащей L и C, при котором U и I совпадают по фазе.

В последовательном R, L, C контуре возникает резонанс напряжений, когда , т.е.

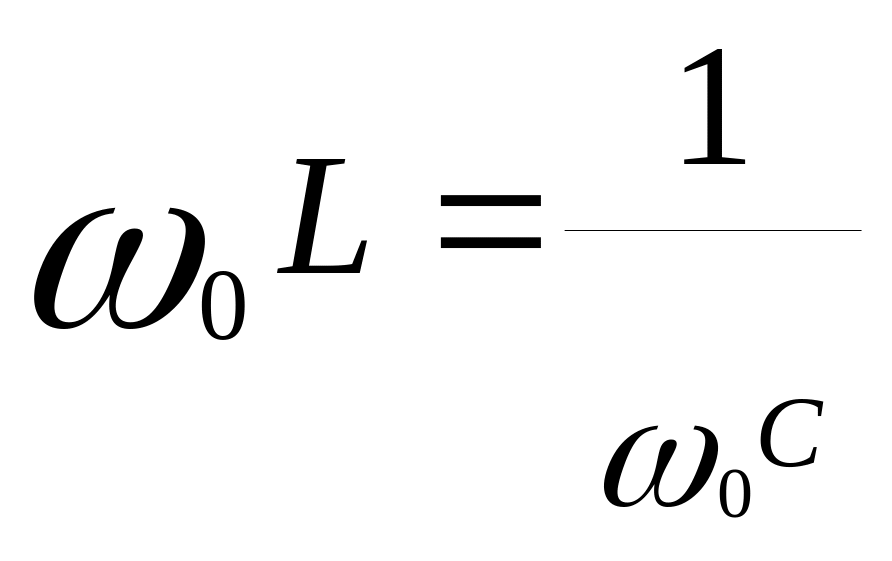(1)

где резонансная угловая частота.

Из (1) следует, что резонанса может достичь, изменяя либо частоту воздействия, либо параметры контура – индуктивность L и емкость C. При резонансе сопротивление реактивных элементов цепи равно:

Входное (эквивалентное) сопротивление контура

При резонансе ( ): .

На резонансной частоте входное сопротивление контура имеет чисто резистивный характер и равно сопротивлению потерь контура R.

Действующее значение тока контура и на резонансной частоте:

;

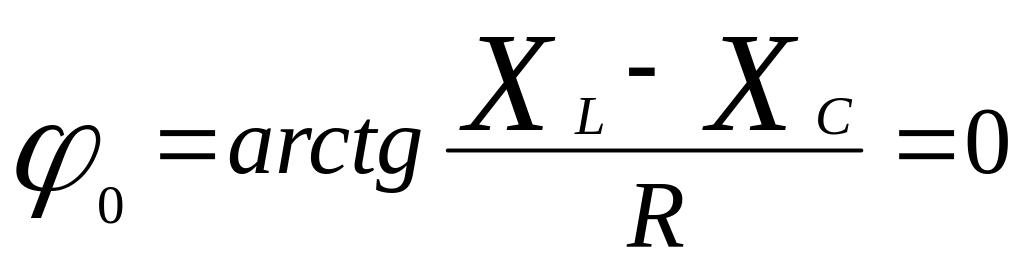
Действующее значение напряжения U на реактивных элементах контура на резонансной частоте определяется произведением характеристического сопротивления на действующее значение тока:

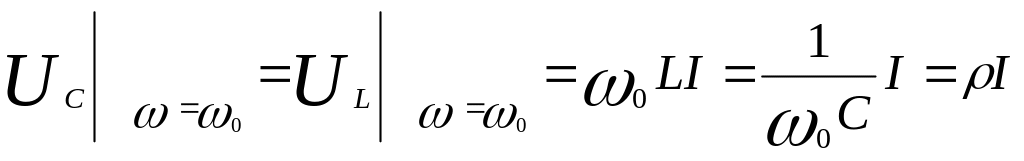
24.Мгновенная и активная мощности

Под воздействием источника гармонических колебаний токи и напряжения на элементах цепи периодически изменяются во времени, колеблется во времени и мгновенная мощность. На каких-то элементах мгновенная мощность в течение времени может принимать как положительные, так и отрицательные значения. И это означает, что существуют интервалы времени, в которые цепь либо потреб­ляет энергию, либо возвращает ее источнику. Рассмотрим энергетические характеристики процессов в цепях гармонического тока и покажем, как можно рассчитывать энергетические зависимости.

Пусть напряжение и ток в любом месте ЭЦ, напряжение на зажимах двухполюсника

измеряется по гармоническому закону:

Тогда мгновенная мощность двухполюсника:

,

где сдвиг фаз между напряжением и током,

UIcosφ – постоянная составляющая зависит от сдвига фаз между током и напряжением.

- переменная составляющая, амплитуда которой UI не зависит от φ.

Среднее значение мгновенной мощности двухполюсника за период есть активная мощность и численно равно постоянной составляющей мгновенной мощности:

Активная мощность характеризует среднюю за период скорость поступления энергии в двухполюсник. По знаку P_A можно судить о направлении передачи энергии: при P_A>0 двухполюсник потребляет энергию, при P_A<0 отдает энергию остальной части цепи. В пассивных двухполюсниках P_A не может быть отрицательной.

Полной мощностью P_S называется величина, равная произведению действующих значений тока и напряжения на зажимах цепи:

Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности. Активная мощность двухполюсника может быть выражена через полную мощность:

(1)

Из выражения (1) видно, что полная мощность есть максимально возможное значение активной мощности цепи, которое имеет место при φ=0.