
- •Камышинский технологический институт (филиал)
- •Задачи по математике для экономистов
- •Волгоград
- •1. Линейная алгебра
- •2. Введение в математический анализ
- •3. Дифференциальное исчисление
- •4. Исследование функции и построение графиков
- •5. Неопределенный интеграл
- •6. Определенный интеграл
- •400131 Волгоград, просп. Им. В. И. Ленина, 28.
- •400131 Волгоград, ул. Советская, 35.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Камышинский технологический институт (филиал)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
КАФЕДРА «ВЫСШАЯ МАТЕМАТИКА»
Задачи по математике для экономистов
Методические указания
РПК «Политехник»
Волгоград
2007
УДК 510 (07)
З – 15
Задачи по математике для экономистов: Методические указания / Сост. Н. Г. Дементьева, В. Ф. Казак, И. Э. Симонова; Волгоград. гос. техн. ун-т. – Волгоград, 2007. – 35 c.
Cодержат задачи по математике. Даны 30 вариантов заданий к типовой работе, методические указания по ее выполнению, образцы решения основных типов задач.
Предназначены для студентов I курса экономических специальностей.
Рецензент: С. В. Мягкова
Табл. 7. Библиогр.: 4 назв.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Волгоградский
государственный
технический
 университет,
2007
университет,
2007
1. Линейная алгебра
Экономический
смысл матрицы:
матрица представляет собой упорядоченную
систему информации, представленную в
виде таблицы. Система информации о
взаимных поставках продукции отраслей
материального производства может быть
представлена в виде матрицы. Пусть
имеется
![]() отраслей производства. Определим
квадратную матрицу
отраслей производства. Определим
квадратную матрицу
![]() размером
размером
![]() ,
элементы которой
,
элементы которой
![]() обозначают объёмы поставок продукции
из
обозначают объёмы поставок продукции
из
![]() отрасли
в
отрасли
в
![]() -ю
отрасль. Матрицей можно представить и
систему информации о нормах материальных
затрат для планирования снабжения
предприятия. Если предприятие производит
типов продукции, используя при этом
-ю
отрасль. Матрицей можно представить и
систему информации о нормах материальных
затрат для планирования снабжения
предприятия. Если предприятие производит
типов продукции, используя при этом
![]() видов сырья, то матрица
видов сырья, то матрица
![]() размера
размера
![]() определяет нормы материальных затрат.
Так,
определяет нормы материальных затрат.
Так,
![]() - норма расхода
-го
вида сырья на производство единицы
-го
типа продукции.
- норма расхода
-го
вида сырья на производство единицы
-го
типа продукции.
Предположим, что
два различных предприятия одной отрасли
производят одинаковые типы продукции
![]() ,
на которую расходуется
видов сырья
,
на которую расходуется
видов сырья
![]() .
В силу различной технологии нормы
материальных затрат на предприятиях
неодинаковы и описываются матрицами
размера
.
В силу различной технологии нормы
материальных затрат на предприятиях
неодинаковы и описываются матрицами
размера
![]() А и
В
соответственно. Пусть первое предприятие
производит
А и
В
соответственно. Пусть первое предприятие
производит
![]() единиц продукции
единиц продукции
![]() ,
,
![]() - типа
- типа
![]() ,
…
,
…
![]() - типа
- типа
![]() .
Второе, соответственно,
.
Второе, соответственно,
![]() единиц продукции. Ставится
единиц продукции. Ставится
Задача 1. Определить матрицу полных материальных затрат в данной отрасли на производство продукции.
Решение. Введём векторы – столбцы производства первого и второго предприятий:
![]() ,
,
![]() .
.
Чтобы найти полные
затраты первого предприятия по каждому
виду сырья, нужно умножить матрицу норм
материальных затрат А
на столбец Х,
АХ =
С (порядок
сомножителей определяется возможностью
перемножения двух матриц и экономическим
смыслом их произведения). Матрица-столбец
С имеет
размер
![]() .
Экономический смысл каждого элемента
.
Экономический смысл каждого элемента
![]() (i
= 1…n)
– полные затраты сырья
(i
= 1…n)
– полные затраты сырья
![]() на всю продукцию, выпускаемую первым
предприятием. Аналогично определяются
полные затраты второго предприятия по
каждому виду сырья: BY
= D,
где матрица-столбец D
тоже имеет размер
.
Полные затраты сырья каждого вида по
обоим предприятиям получаются
суммированием матриц С
и D:
P
= C+D.
Экономический смысл каждого элемента
на всю продукцию, выпускаемую первым
предприятием. Аналогично определяются
полные затраты второго предприятия по
каждому виду сырья: BY
= D,
где матрица-столбец D
тоже имеет размер
.
Полные затраты сырья каждого вида по
обоим предприятиям получаются
суммированием матриц С
и D:
P
= C+D.
Экономический смысл каждого элемента
![]() (i
= 1…n)
– полные затраты сырья
на всю продукцию, выпускаемую двумя
предприятиями. В матричном виде P
= AX+BY.
(i
= 1…n)
– полные затраты сырья
на всю продукцию, выпускаемую двумя
предприятиями. В матричном виде P
= AX+BY.
Задачи.
1. Определить матрицу полных затрат, если в условиях задачи 1
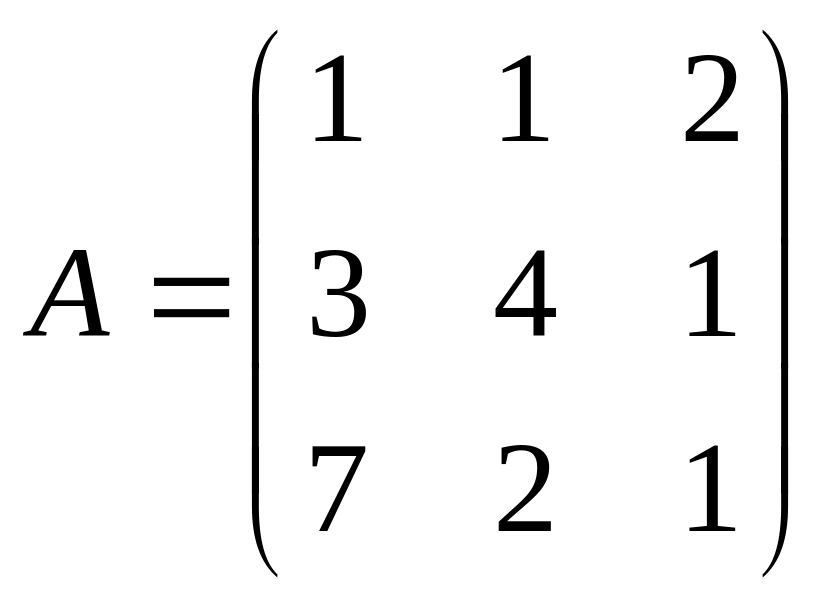 ,
,
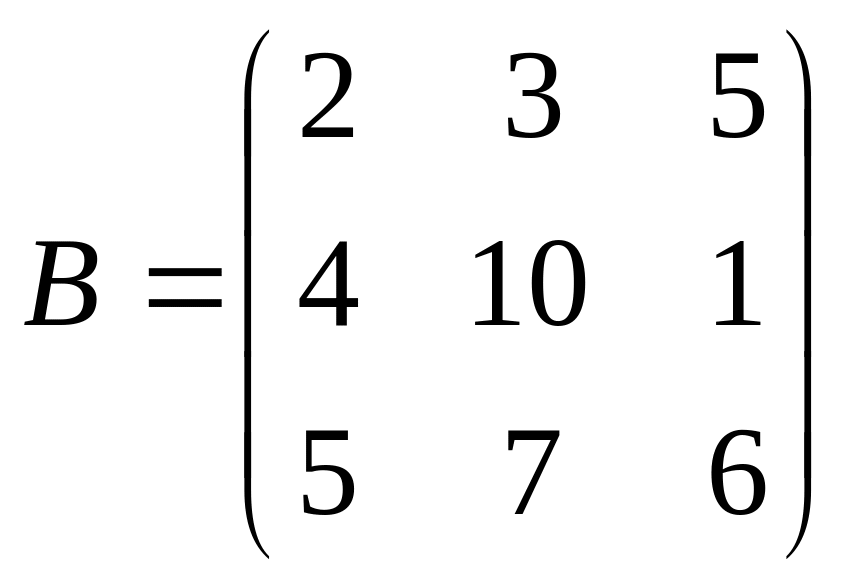 ,
,
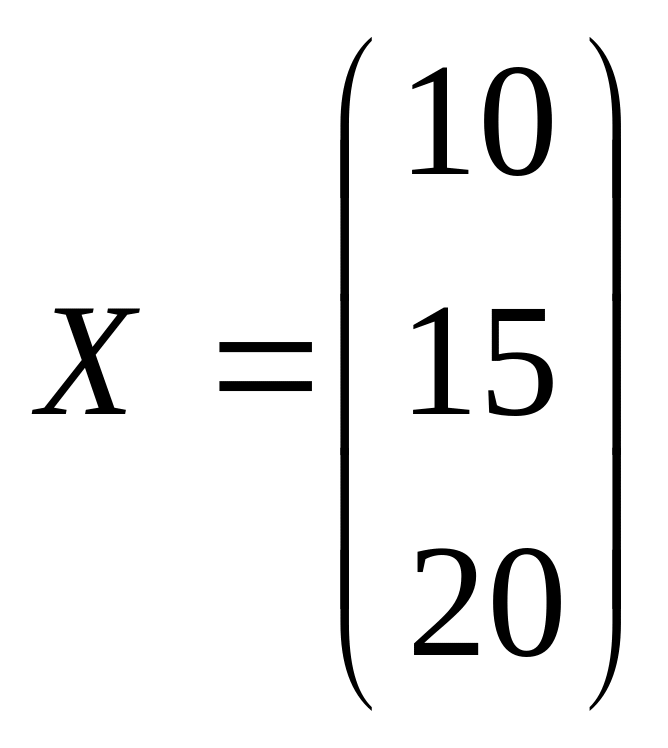 ,
,
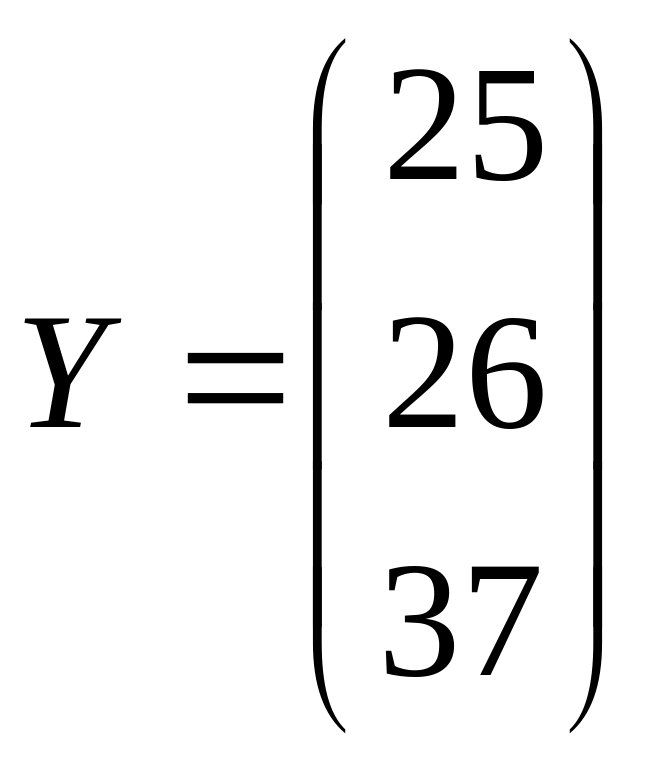 .
.
Пояснить экономический смысл.
2. Определить матрицу полных затрат, если в условиях задачи 1
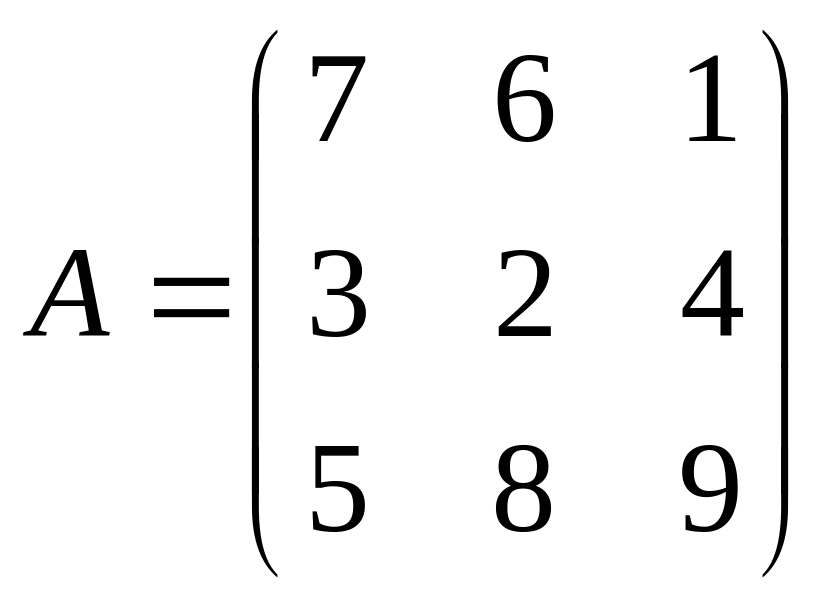 ,
,
 ,
,
 ,
,
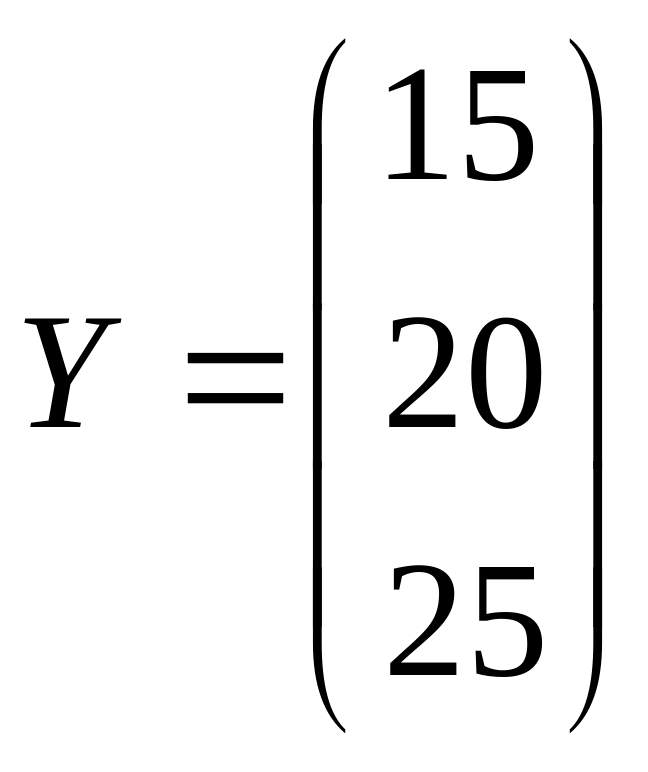 .
.
Пояснить экономический смысл.
3. Определить матрицу полных затрат, если в условиях задачи 1
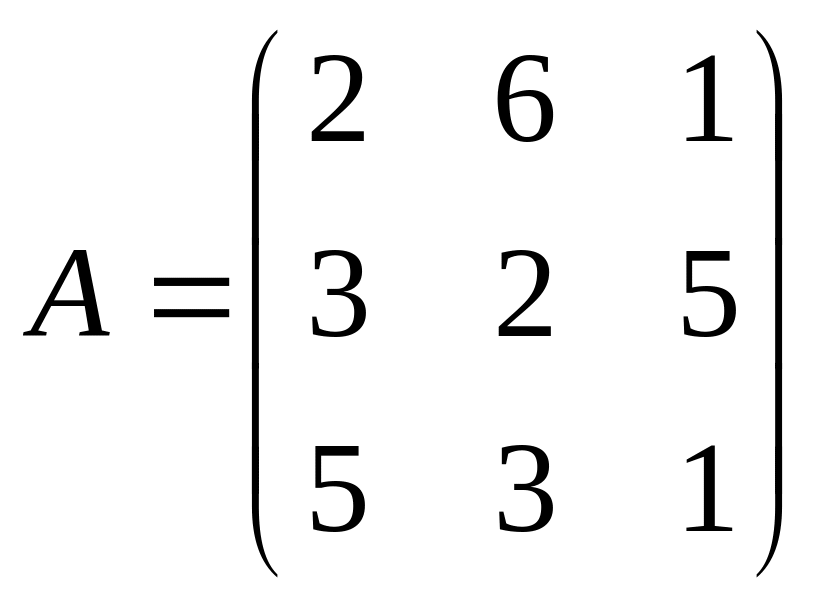 ,
,
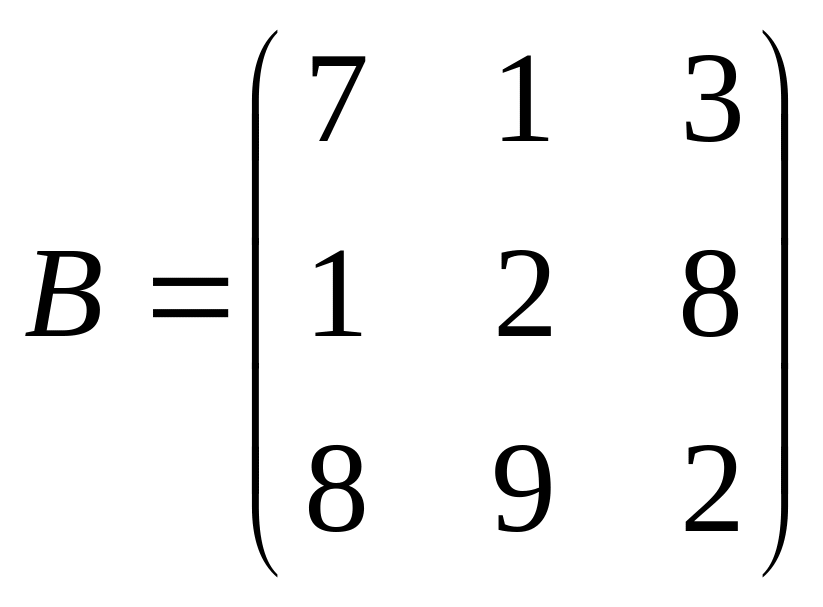 ,
,
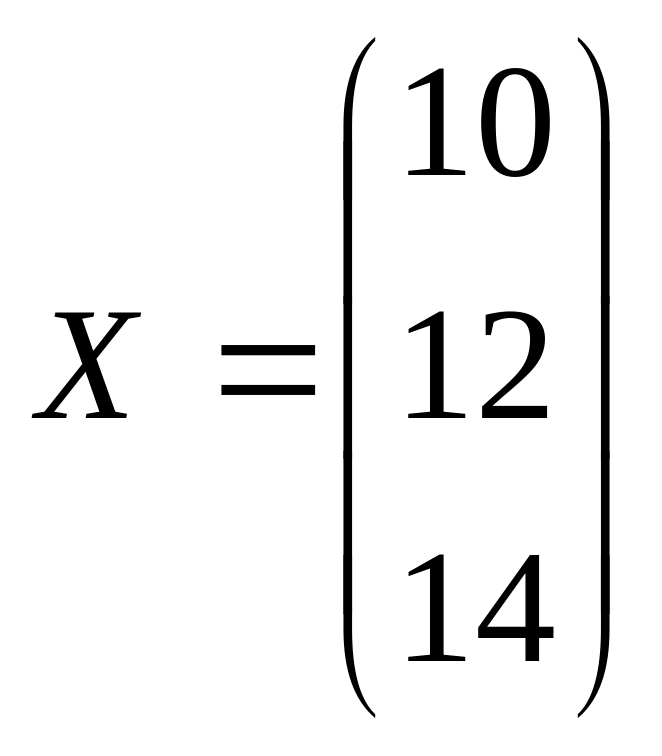 ,
,
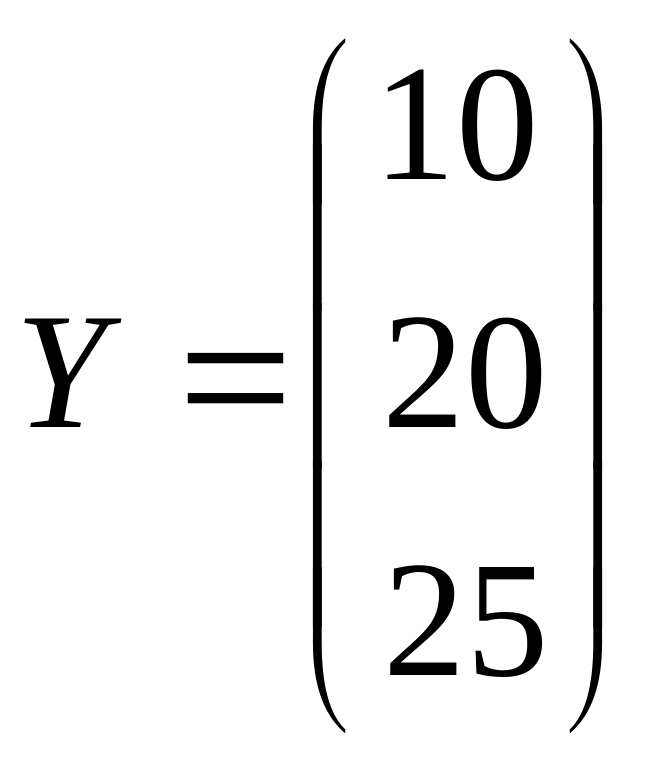 .
.
Пояснить экономический смысл.
4. Два предприятия
выпускают 3 вида мебельных гарнитуров,
расходуя при этом 4 вида сырья: фанеру,
пластмассу, ткань, древесину. Нормы
материальных затрат для каждого
предприятия заданы матрицами А и В.
Первое предприятие выпустило 100 гарнитуров
1-го типа,
100 гарнитуров 2-го типа, 0 гарнитуров 3-го
типа. Второе предприятие выпустило,
соответственно, 300, 200, 100 гарнитуров.
Найти матрицу полных затрат, если
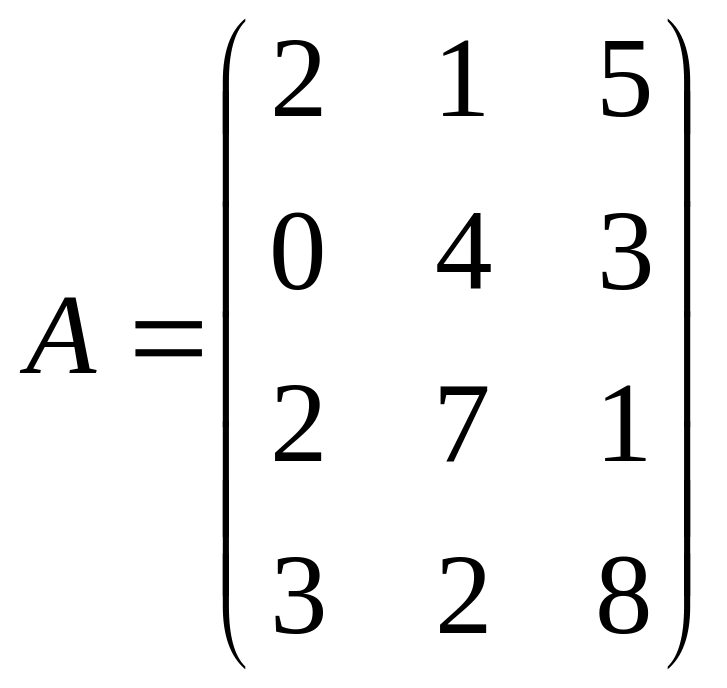 ,
,
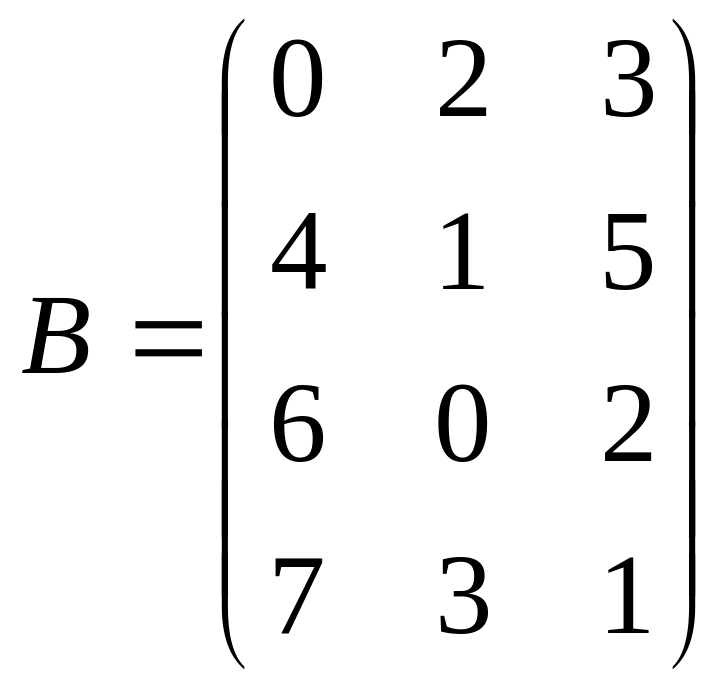
5. Используя условие
предыдущей задачи, найти матрицу
материальных затрат, если
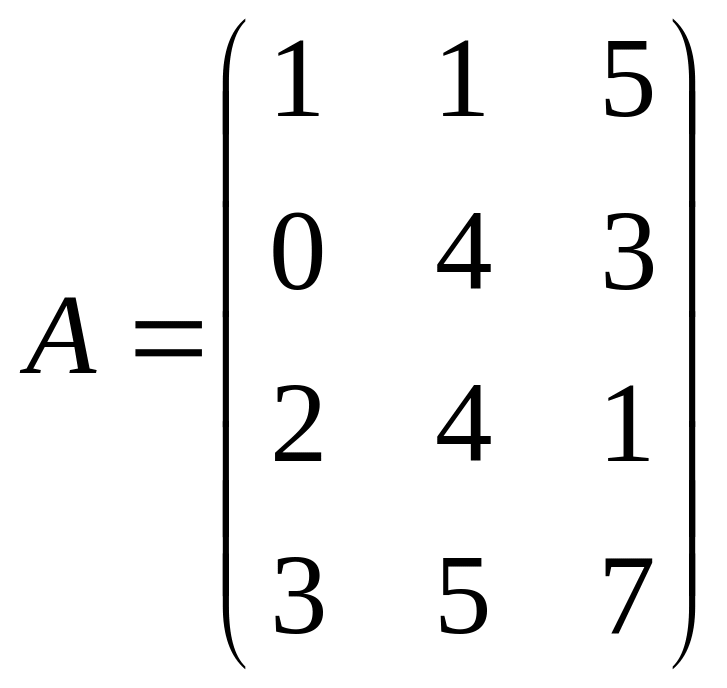 ,
,
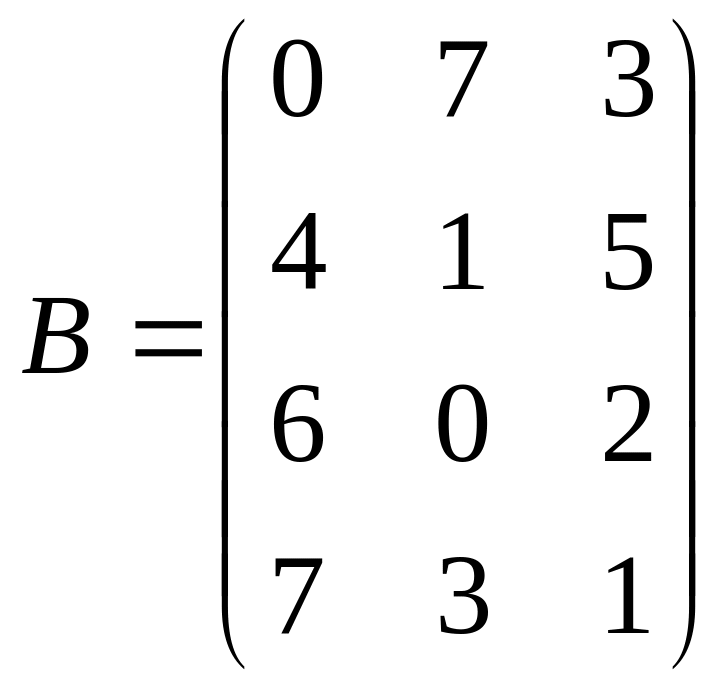
6. Два предприятия выпускают 3 типа мебельных гарнитуров, расходуя при этом 4 вида сырья: фанеру, пластмассу, ткань, древесину. Нормы материальных затрат заданы для каждого предприятия матрицами А и В. Первое предприятие выпустило 120 гарнитуров 1-го типа, 0 гарнитуров 2-го типа, 210 гарнитуров 3-го типа. Второе предприятие выпустило, соответственно, 400, 200, 300 гарнитуров.
Найти матрицу
полных затрат, если
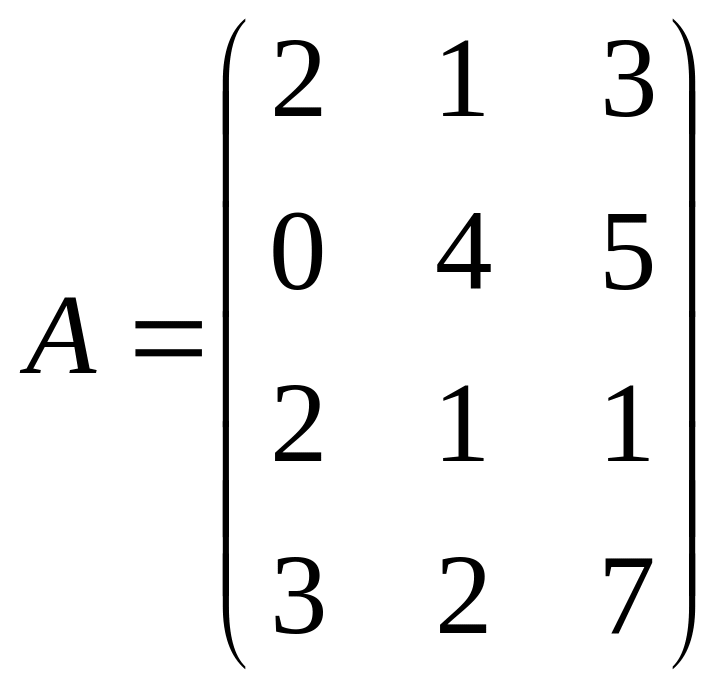 ,
,
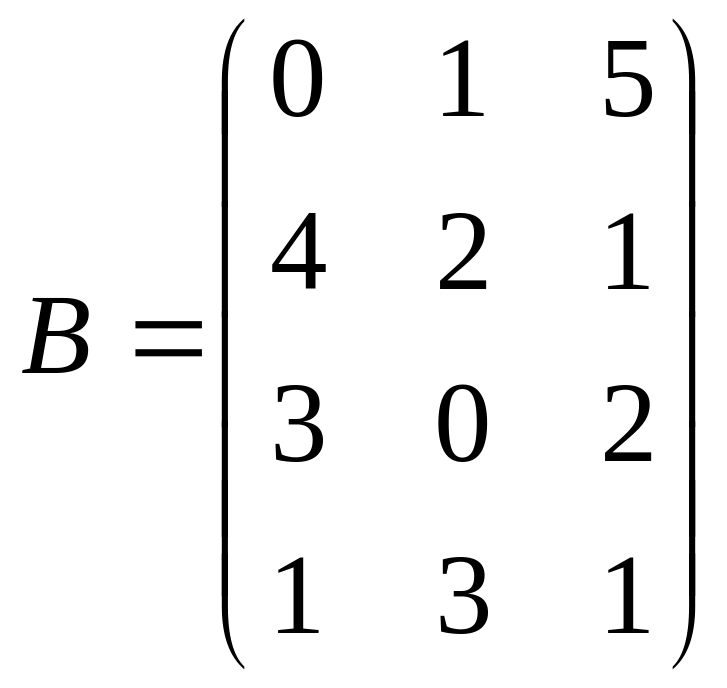
7. Используя условие
предыдущей задачи, найти матрицу
материальных затрат, если
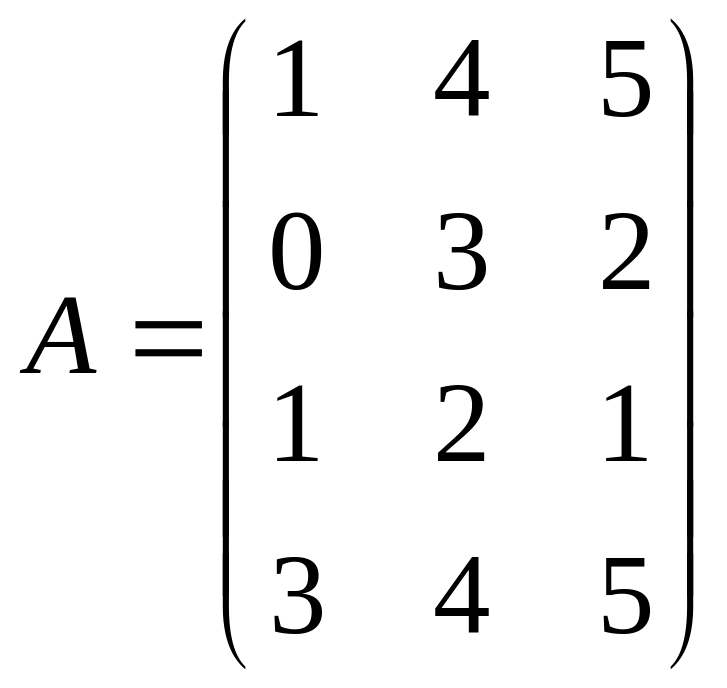 ,
,
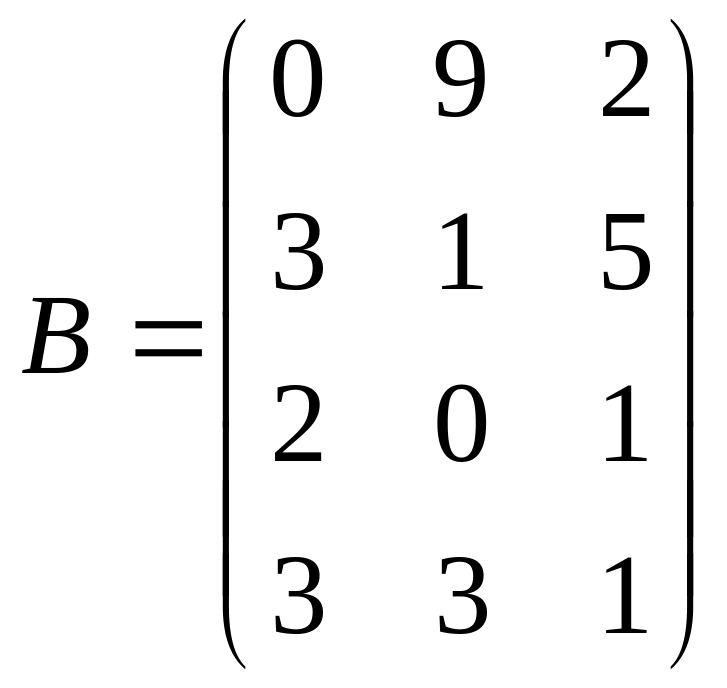
Задача 2.
В городе имеются ателье индивидуального
пошива женского лёгкого платья первого,
второго и третьего разрядов. Каждое
ателье изготавливает 4 вида изделий:
юбки, платья, блузки, брюки. Ателье s
разряда за изготовление изделия i
вида получает
![]() рублей. Матрица расценок
рублей. Матрица расценок
![]() ,
s
= 1,2,3,4;
i
= 1,2,3,4.
Существует единый поквартальный план
пошива для ателье всех разрядов, который
задаётся матрицей
,
s
= 1,2,3,4;
i
= 1,2,3,4.
Существует единый поквартальный план
пошива для ателье всех разрядов, который
задаётся матрицей
![]() ,
i,j
= 1,2,3,4, где
,
i,j
= 1,2,3,4, где
![]() -
количество изделий i
вида, которое
каждое ателье должно изготовить в j
квартале.
Требуется определить матрицу Т
поквартальной
выручки ателье каждого разряда.
-
количество изделий i
вида, которое
каждое ателье должно изготовить в j
квартале.
Требуется определить матрицу Т
поквартальной
выручки ателье каждого разряда.
Решение.
Пусть
![]() - выручка ателье s-разряда
в j-квартале
s=1,2,3,4;
j=1,2,3,4
– элементы матрицы Т.
Тогда
- выручка ателье s-разряда
в j-квартале
s=1,2,3,4;
j=1,2,3,4
– элементы матрицы Т.
Тогда
![]()
![]() ,
где каждое слагаемое определяет
квартальную выручку ателье от изделий
соответствующего вида. По правилу
умножения матриц можем записать в
матричном виде: T
= DP,
т.е. матрица поквартальной выручки
определяется как произведение матрицы
расценок D
на матрицу
поквартального плана Р.
Ответ:
T=DP.
,
где каждое слагаемое определяет
квартальную выручку ателье от изделий
соответствующего вида. По правилу
умножения матриц можем записать в
матричном виде: T
= DP,
т.е. матрица поквартальной выручки
определяется как произведение матрицы
расценок D
на матрицу
поквартального плана Р.
Ответ:
T=DP.
8. Найти матрицу поквартальной выручки ателье, если матрица расценок
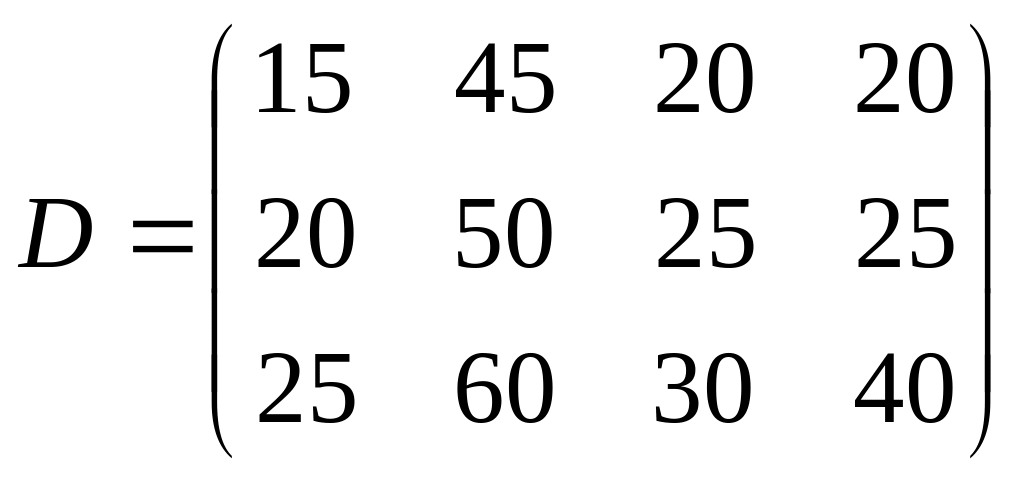 ,
,
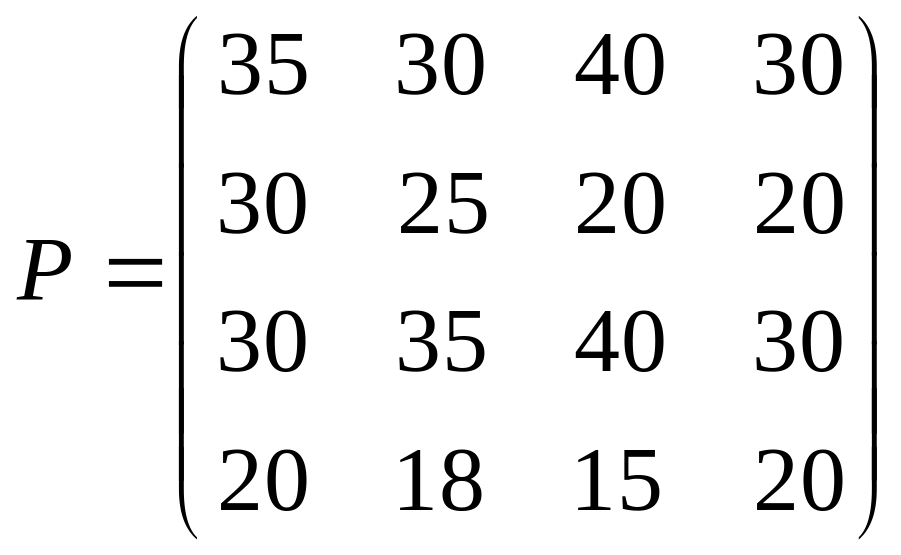 - матрица поквартального плана. Провести
анализ результатов.
- матрица поквартального плана. Провести
анализ результатов.
9. Найти матрицу поквартальной выручки ателье, если матрица расценок
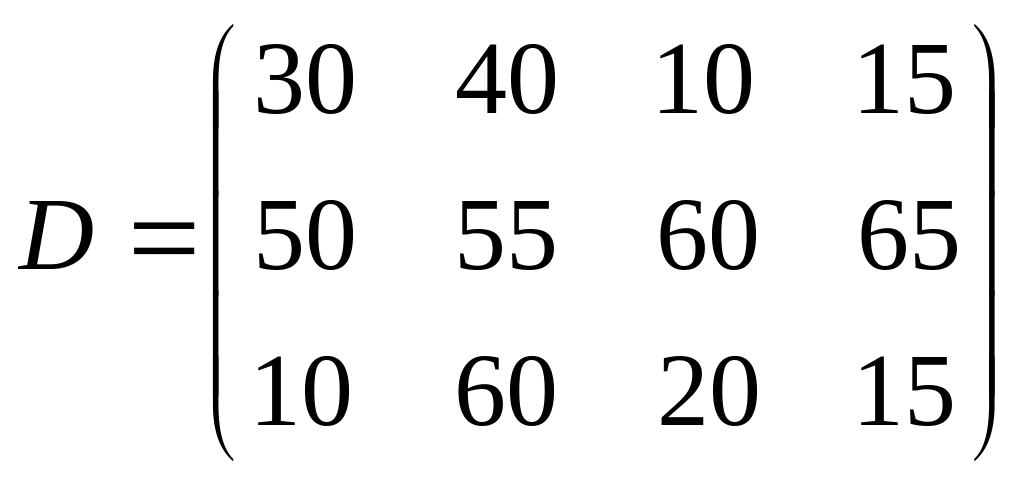 ,
,
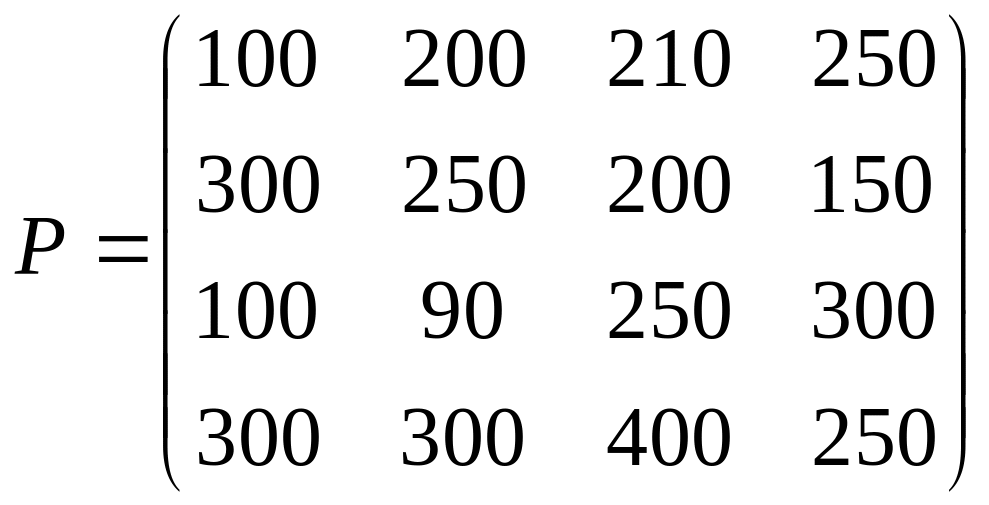 - матрица поквартального плана.
- матрица поквартального плана.
Провести анализ результатов.
10. Найти матрицу поквартальной выручки ателье, если матрица расценок
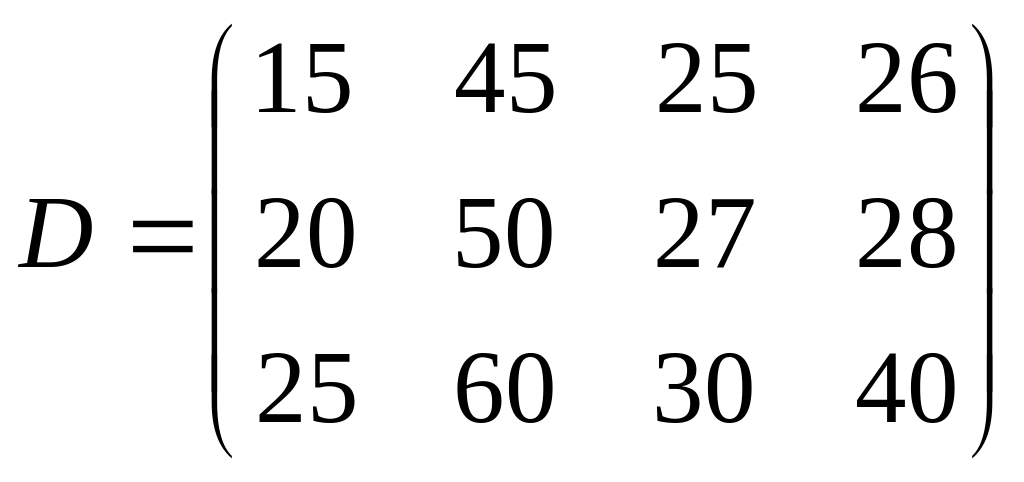 ,
,
 - матрица поквартального плана.
- матрица поквартального плана.
Провести анализ результатов.
11. Найти матрицу поквартальной выручки ателье, если матрица расценок
 ,
,
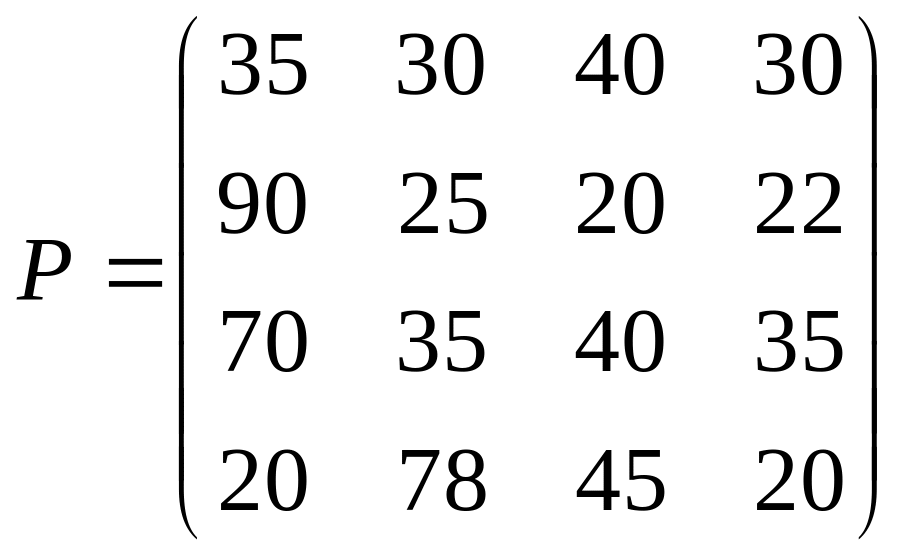 - матрица поквартального плана.
- матрица поквартального плана.
Провести анализ результатов.
12. Найти матрицу поквартальной выручки ателье, если матрица расценок
 ,
,
 - матрица поквартального плана.
- матрица поквартального плана.
Провести анализ результатов.
13. Найти матрицу поквартальной выручки ателье, если матрица расценок
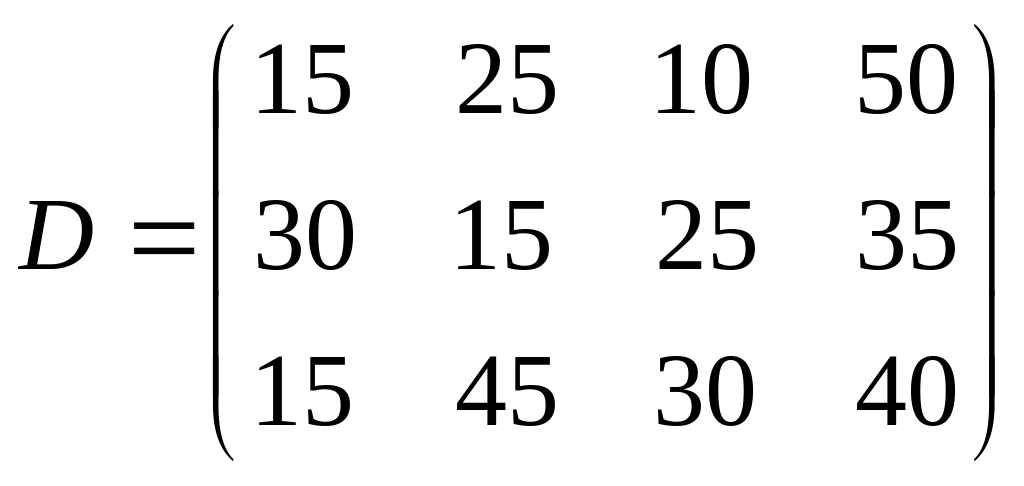 ,
,
 - матрица поквартального плана.
- матрица поквартального плана.
Провести анализ результатов.
14. Для изготовления
трёх видов изделий необходимы детали
трёх типов, потребности в которых заданы
в таблице 1. Потребности в сырье для
изготовления деталей заданы в таблице
2. Определить
потребности в сырье для изготовления
- изделий 1-го вида,
- изделий 2-го
вида,
![]() - изделий 3-го вида.
- изделий 3-го вида.
Материал |
Тип детали |
||
1 |
2 |
3 |
|
Дерево |
1 |
0 |
2 |
Сталь |
0 |
1 |
3 |
Детали |
Вид изделий |
||
1 |
2 |
3 |
|
1.Втулка |
5 |
3 |
2 |
2.Колесо |
4 |
6 |
2 |
3.Корпус |
1 |
1 |
1 |
Задача 3.
Три цеха предприятия выпускают продукцию
3-х видов. Часть продукции идёт на
внутреннее потребление, остальная часть
является конечным продуктом. Требуется
выявить распределение между цехами
продукции, идущей на внутреннее
потребление и общие (валовые) объёмы
выпускаемой продукции (![]() ),
если заданы матрица коэффициентов
прямых материальных затрат и вектор
конечной (валовой) продукции Y:
),
если заданы матрица коэффициентов
прямых материальных затрат и вектор
конечной (валовой) продукции Y:
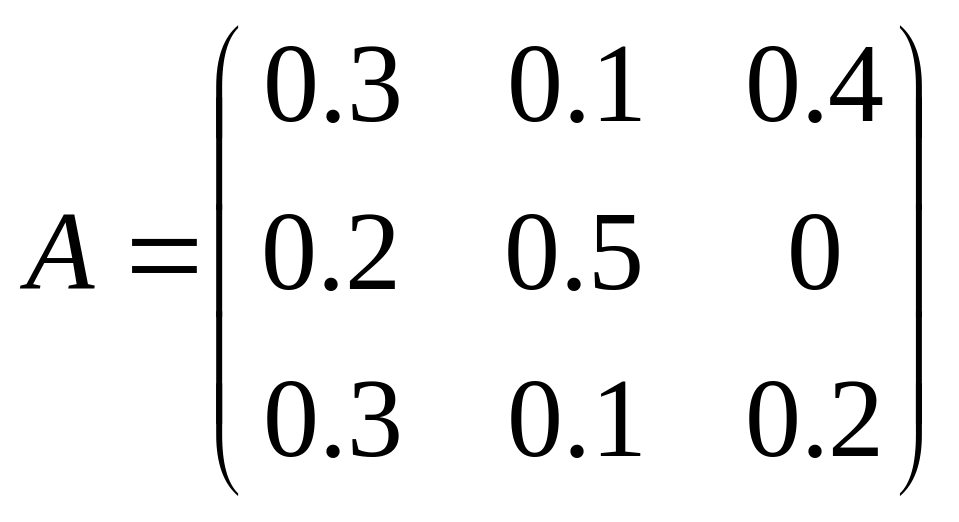
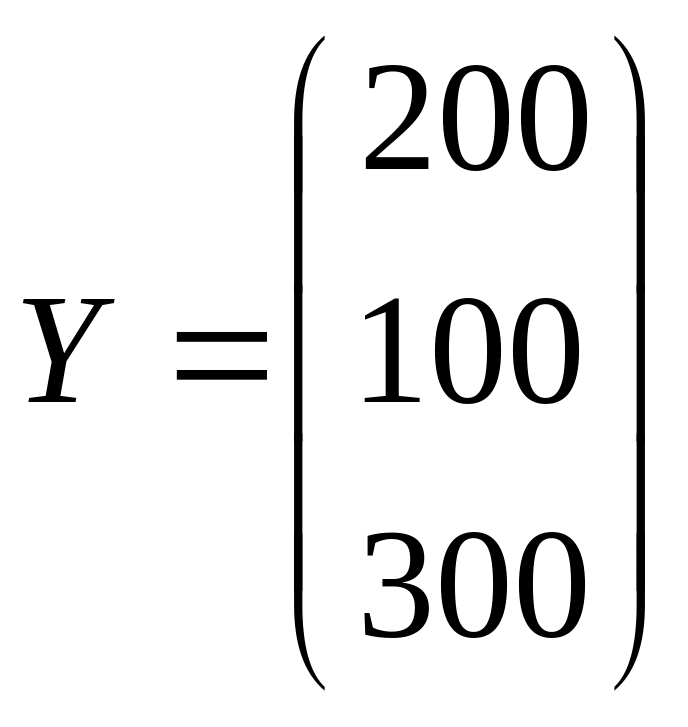 .
.
Заполнить таблицу межотраслевого баланса (МБ).
Решение.
Поскольку выпускаемый продукт Х
используется
как для внутреннего потребления в
количестве АХ,
где А
– матрица прямых затрат, так и в качестве
конечного продукта Y,
то справедливо матричное уравнение X
– AX
= Y
или (Е - А)Х =
Y
(где Е
– единичная матрица). Решение этого
уравнения находится по формуле
![]() .
.
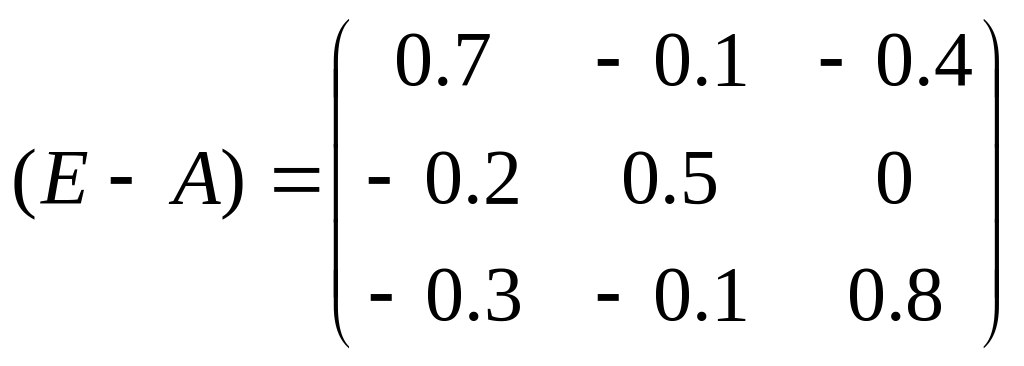 ,
,
 ,
,
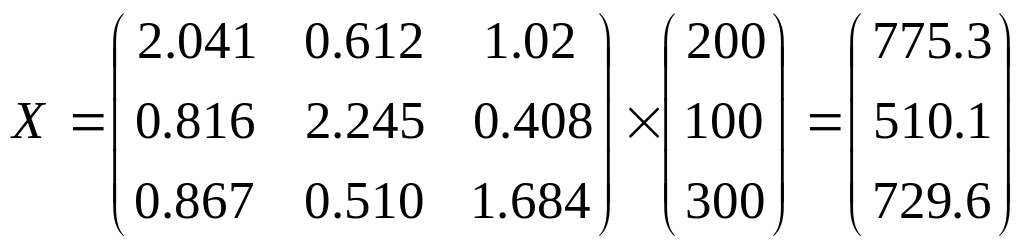 .
.
Таблица межотраслевого баланса (МБ), имеет вид:
Таблица 3
Продукция Цеха |
1 |
2 |
3 |
Конечная продукция |
Валовая продукция |
1 |
232.6 |
51 |
291.8 |
200 |
775.3 |
2 |
155.1 |
255 |
0 |
100 |
510.1 |
3 |
232.6 |
51 |
145.9 |
300 |
729.6 |
Условно – чистый продукт |
155 |
153.1 |
291.9 |
600 |
|
Валовая продукция |
775.3 |
510.1 |
729.6 |
|
2015 |
15. Для трех отраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
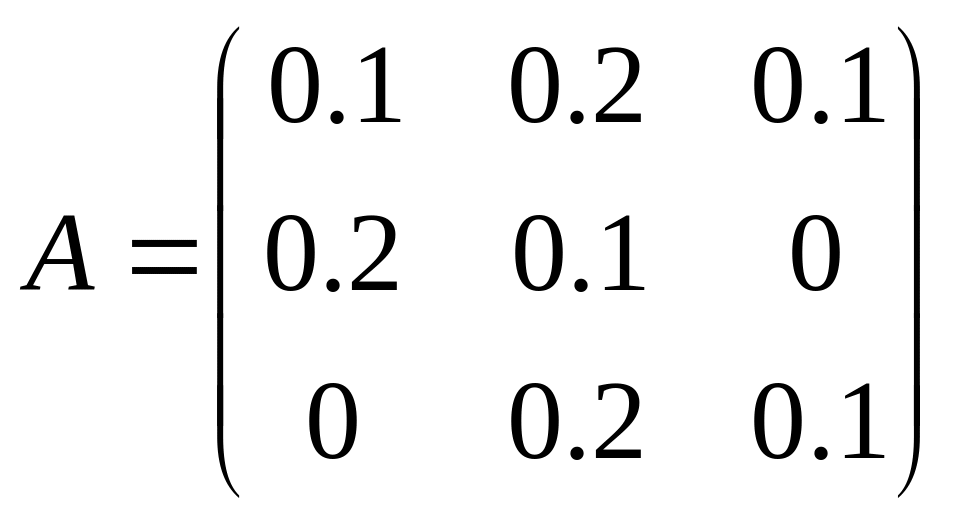 и
и
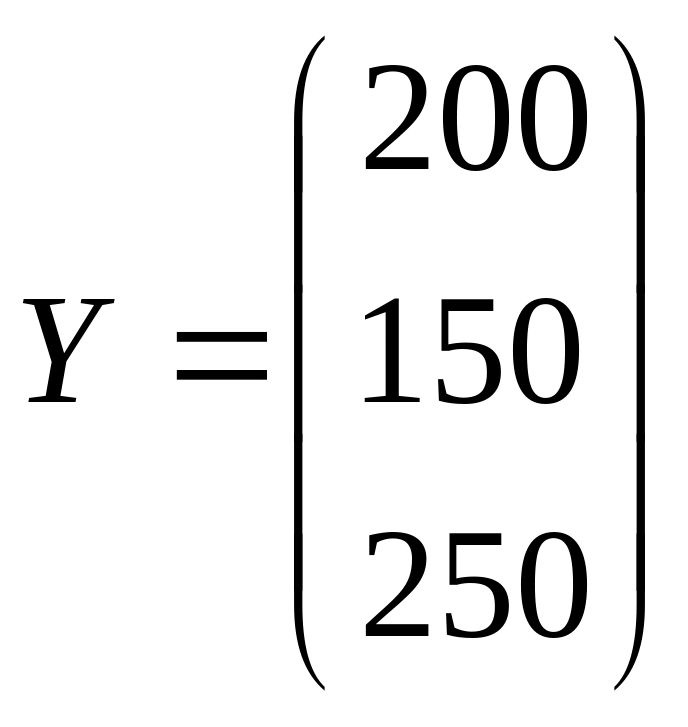 - вектор конечной продукции.
- вектор конечной продукции.
Найти коэффициенты полных материальных затрат и вектор валовой продукции. Заполнить таблицу МБ.
16. Используя условие
задачи 3,
выявить распределение между цехами
продукции, идущей на внутреннее
потребление, и общие (валовые) объёмы
выпускаемой продукции (![]() ),
если
),
если
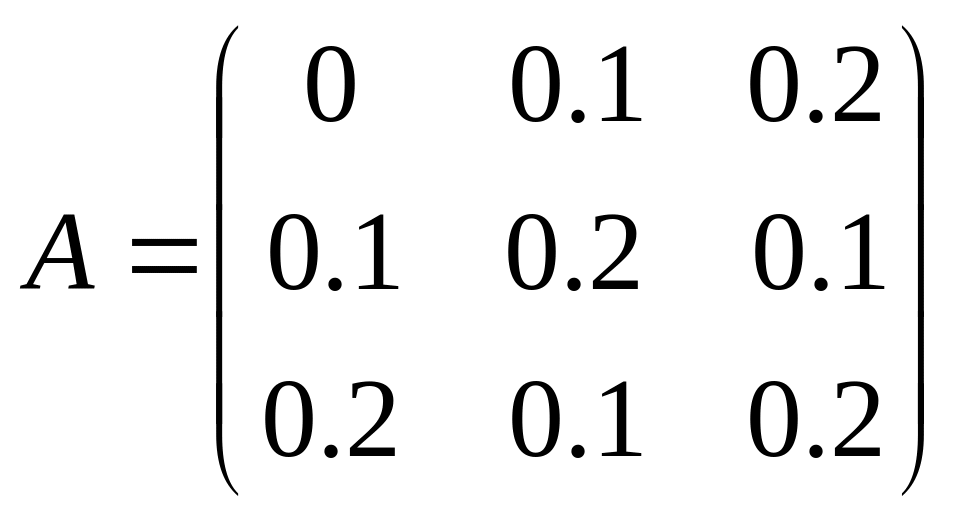 и
и
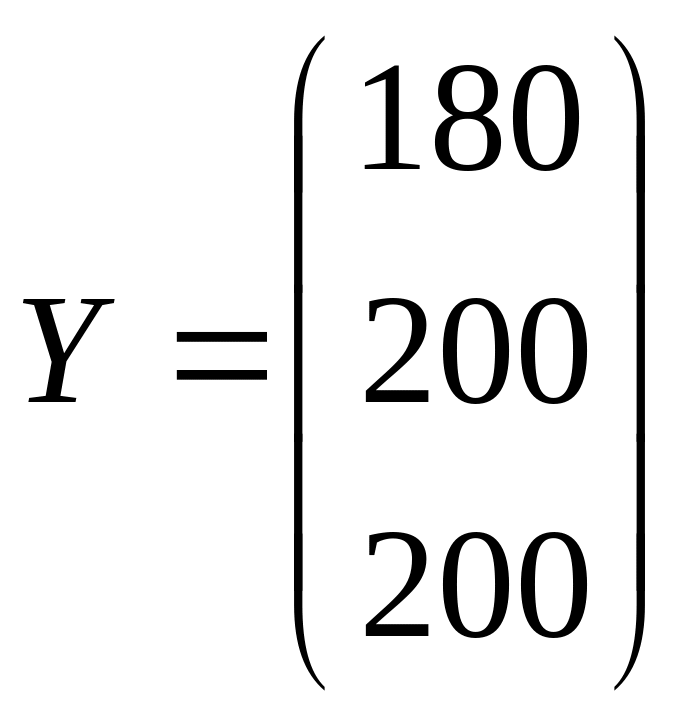 .
Результаты занести в таблицу МБ.
.
Результаты занести в таблицу МБ.
17. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
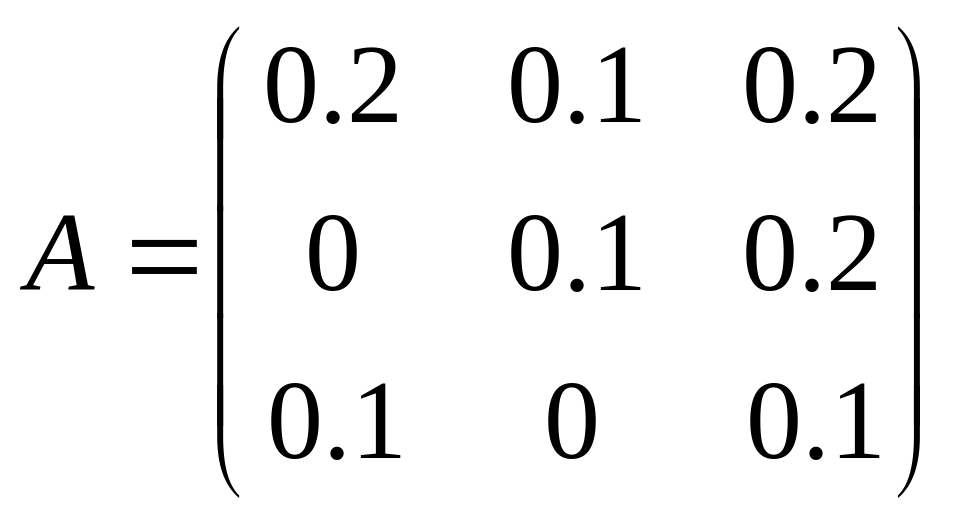 и
и
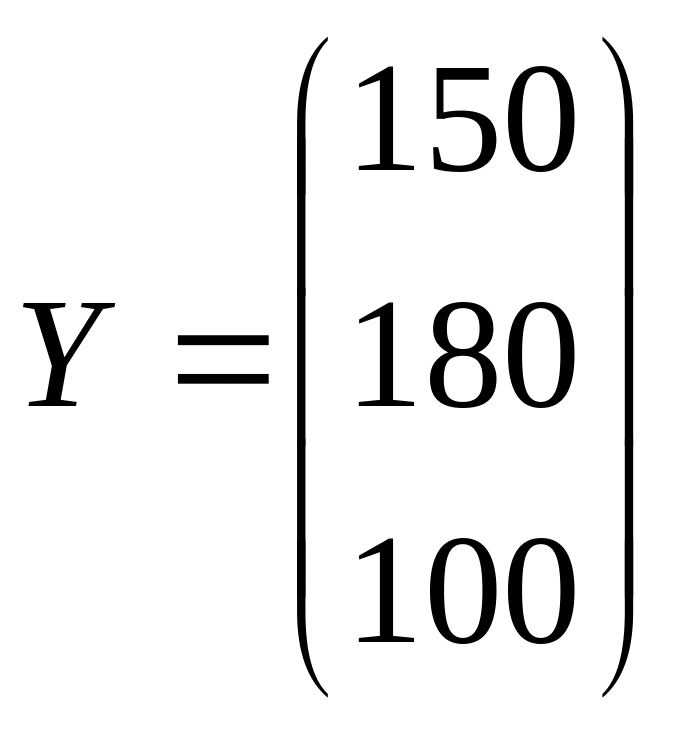 - вектор конечной продукции.
- вектор конечной продукции.
Найти коэффициенты полных материальных затрат и вектор валовой продукции. Результаты занести в таблицу МБ.
18. Для трех отраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
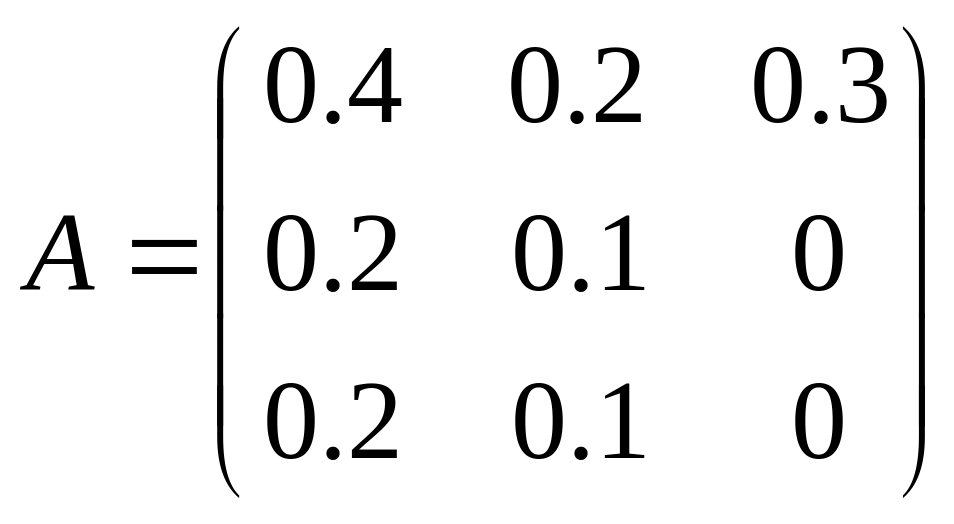 и
и
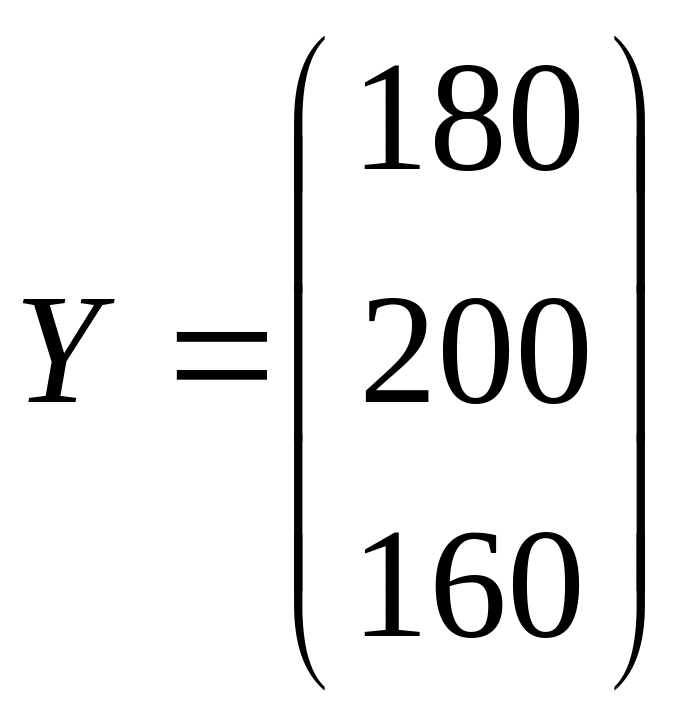 - вектор конечной продукции.
- вектор конечной продукции.
Найти коэффициенты полных материальных затрат и вектор валовой продукции. Результаты занести в таблицу МБ.
19. Для трех отраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
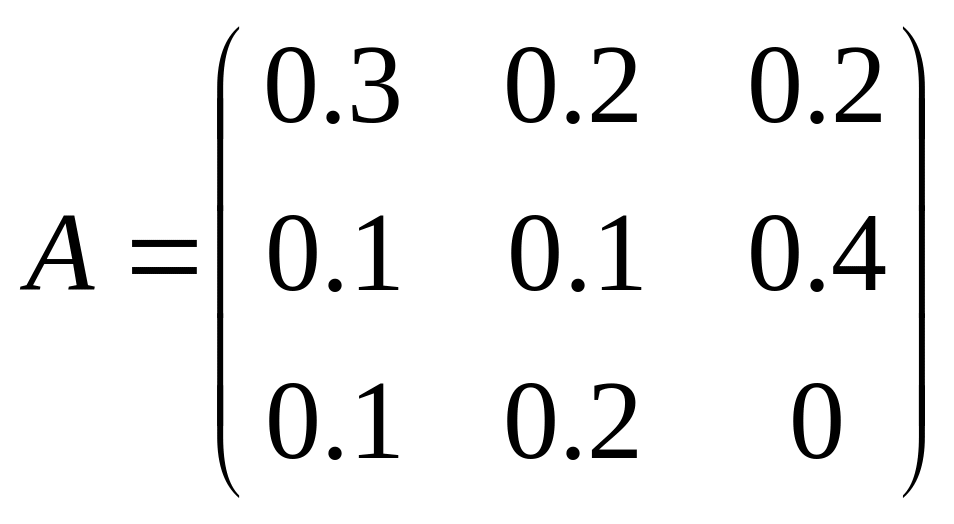 и
и
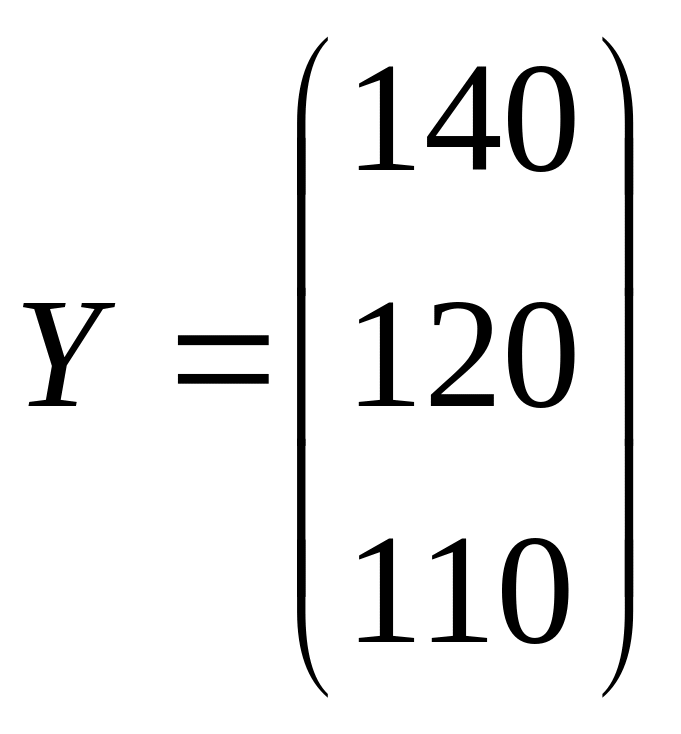 - вектор конечной продукции.
- вектор конечной продукции.
Найти коэффициенты полных материальных затрат и вектор валовой продукции. Результаты занести в таблицу МБ.
20. Для трех отраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
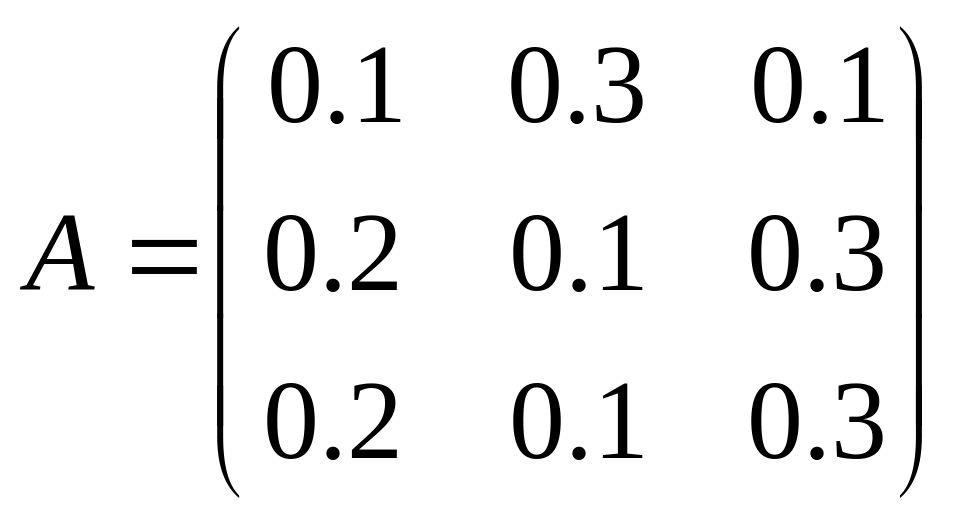 и
и
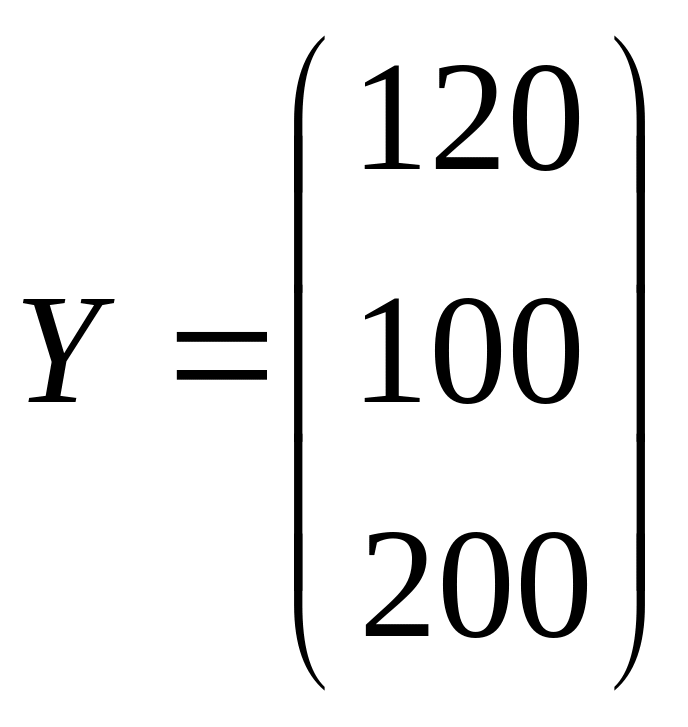 - вектор конечной продукции.
- вектор конечной продукции.
Найти коэффициенты полных материальных затрат и вектор валовой продукции. Результаты занести в таблицу МБ.
21. Для трех отраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
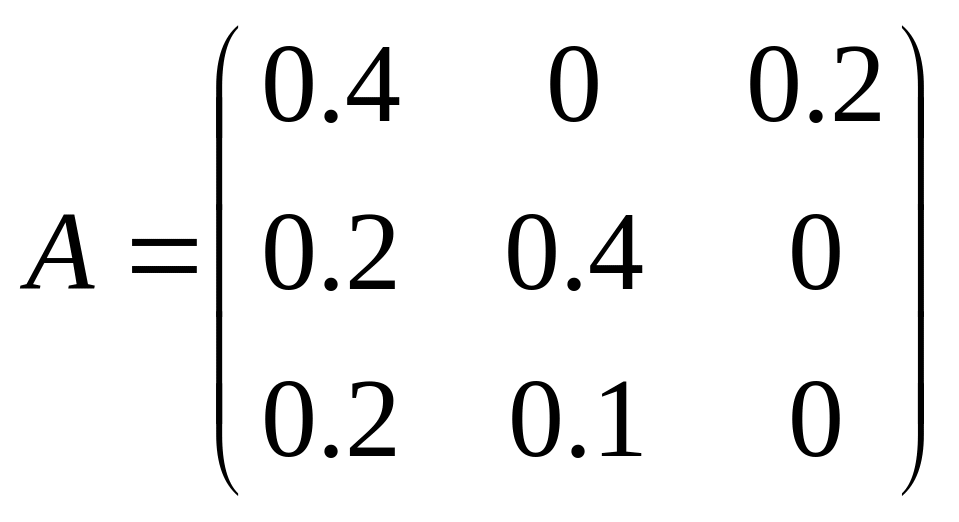 и
и
 - вектор конечной продукции.
- вектор конечной продукции.
Найти коэффициенты полных материальных затрат и вектор валовой продукции. Результаты занести в таблицу МБ.
22. Данные о реализации товаров в 3-х магазинах предоставлены матрицами
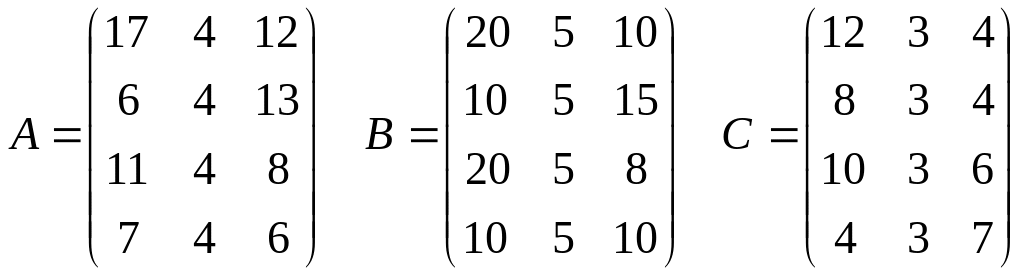
В строках указаны суммы, вырученные за каждый сезон (весна, лето осень, зима), а в столбцах – выручка о продажи трех видов товаров (платья, костюмы, обувь). Требуется: 1) показать, что каждый сезон первый и третий магазины, вместе взятые, продали товаров каждого вида на сумму, большую, чем второй магазин; 2) найти общие суммы продажи всех трех магазинов (по сезонам и всего).
23. В трех торговых
точках проведена ревизия и получены
следующие данные о продаже трех видов
товаров (в условных единицах):
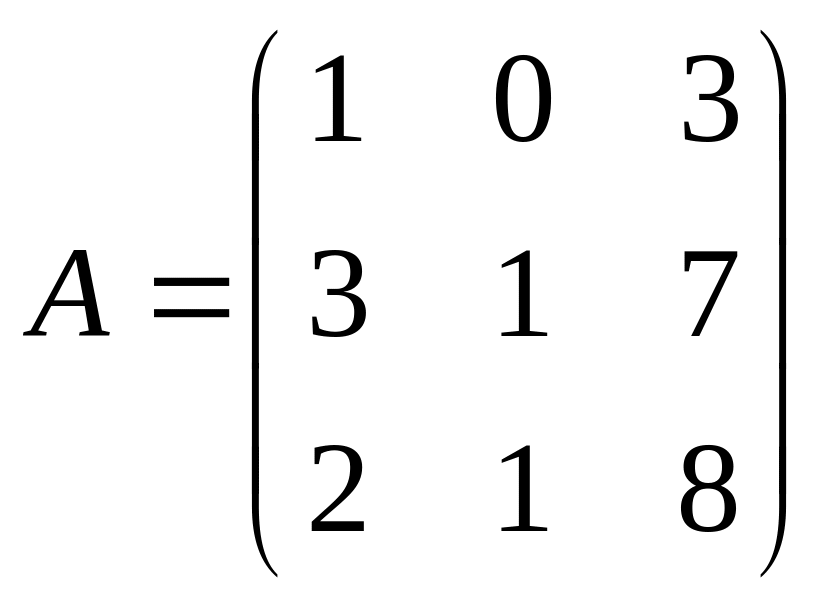 .
В кассе 1-го магазина обнаружено 31.8
условных единиц, 2-го – 154.6 у.е., 3-го –
141.1 у.е. Требуется определить, по какой
цене продавался каждый вид товаров (с
тем, чтобы сравнить эти цены с имеющимися
в накладных).
.
В кассе 1-го магазина обнаружено 31.8
условных единиц, 2-го – 154.6 у.е., 3-го –
141.1 у.е. Требуется определить, по какой
цене продавался каждый вид товаров (с
тем, чтобы сравнить эти цены с имеющимися
в накладных).
24. Предприятие
выпускает три типа игрушек в количестве,
характеризуемом вектор-планом X=(10,7,4).
Для изготовления используется 5 видов
сырья. Задана матрица
![]()
![]() ;
;
![]() ,
где
,
где
![]() характеризует расход
-го
сырья на единицу
-го
вида продукции:
характеризует расход
-го
сырья на единицу
-го
вида продукции:
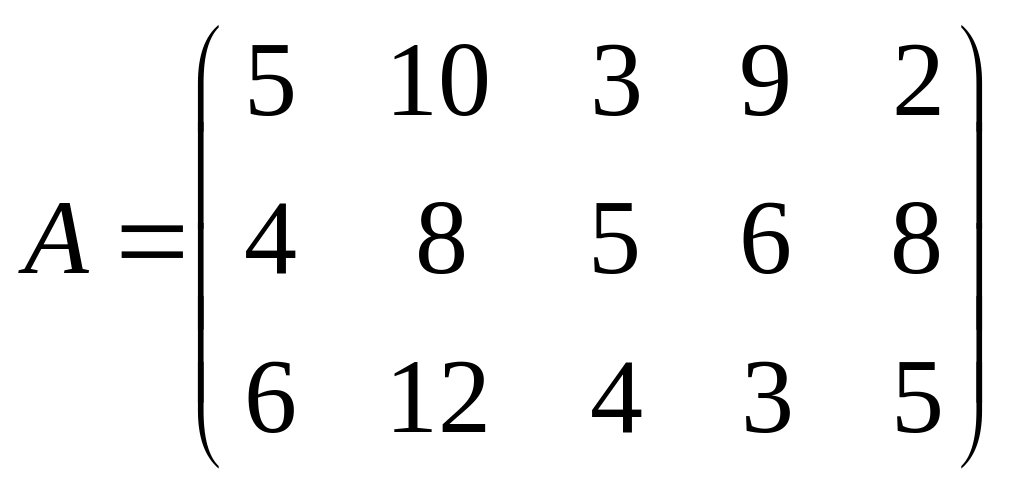
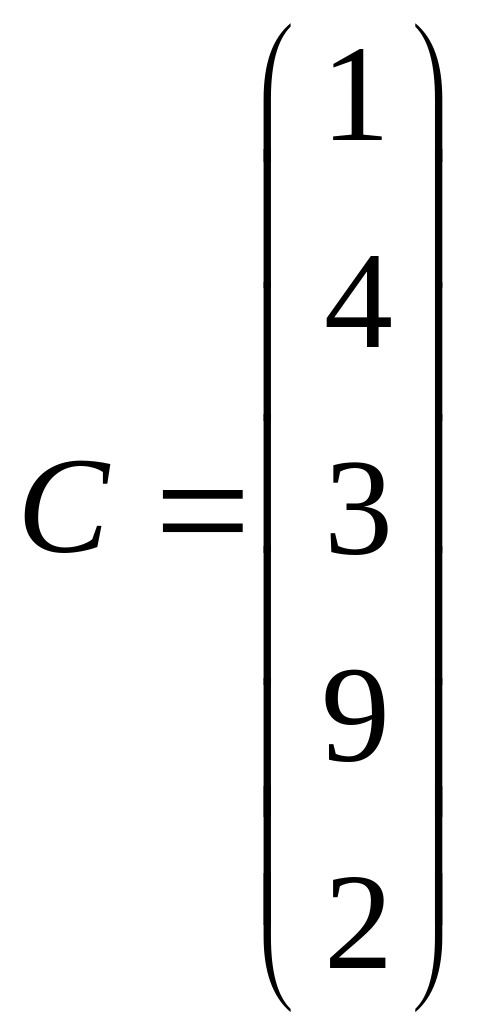 - вектор стоимости
единицы каждого вида сырья. Определить
необходимое количество каждого вида
сырья для обеспечения плана (B),
стоимость сырья для единицы каждого
вида продукции (D)
и общую стоимость всего сырья для всей
продукции (Q).
Указание.
B=XA,
D=AC,
Q=XD.
- вектор стоимости
единицы каждого вида сырья. Определить
необходимое количество каждого вида
сырья для обеспечения плана (B),
стоимость сырья для единицы каждого
вида продукции (D)
и общую стоимость всего сырья для всей
продукции (Q).
Указание.
B=XA,
D=AC,
Q=XD.
25. Предприятие выпускает три типа игрушек в количестве, характеризуемом вектор-планом X=(9,8,3). Для изготовления используется 5 видов сырья. Задана матрица
; , где характеризует расход -го сырья на единицу -го вида продукции:
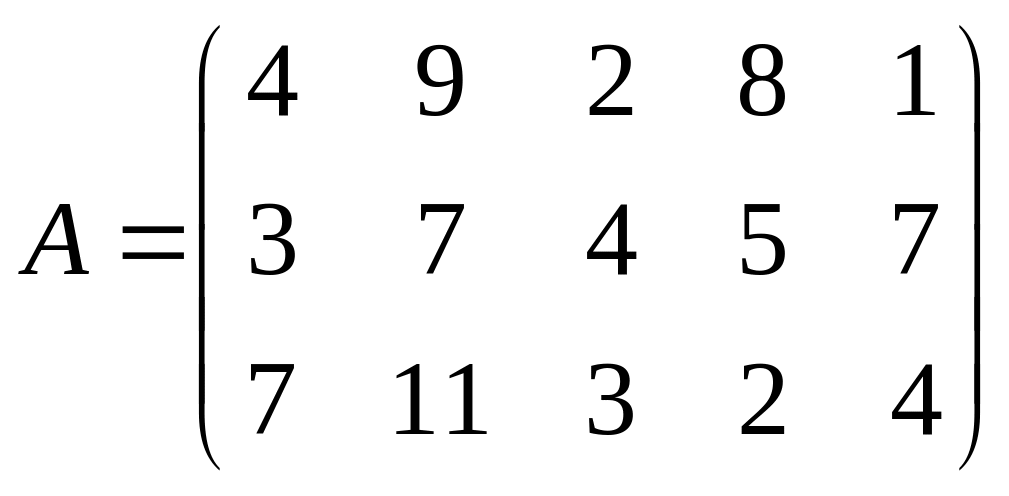
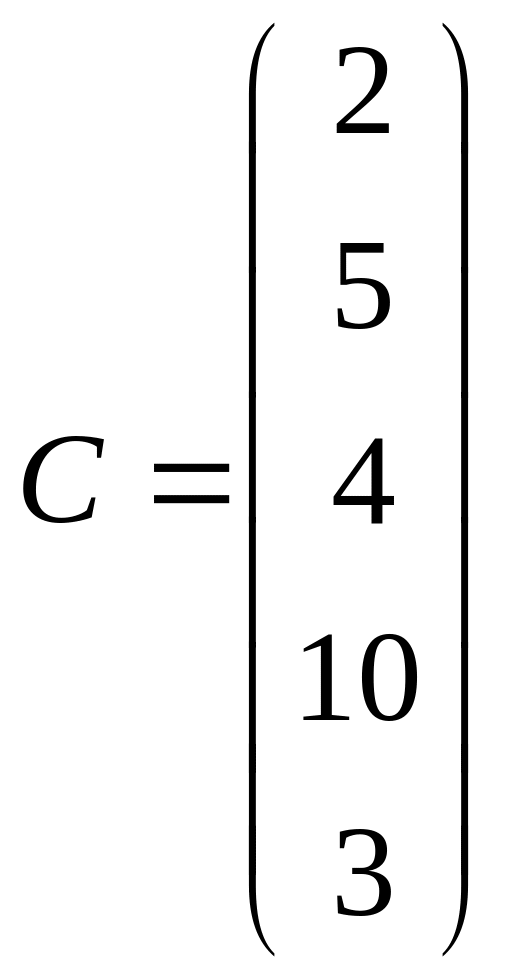 - вектор стоимости
единицы каждого вида сырья. Определить
необходимое количество каждого вида
сырья для обеспечения плана (B),
стоимость сырья для единицы каждого
вида продукции (D)
и общую стоимость всего сырья для всей
продукции (Q).
Указание.
B=XA,
D=AC,
Q=XD.
- вектор стоимости
единицы каждого вида сырья. Определить
необходимое количество каждого вида
сырья для обеспечения плана (B),
стоимость сырья для единицы каждого
вида продукции (D)
и общую стоимость всего сырья для всей
продукции (Q).
Указание.
B=XA,
D=AC,
Q=XD.
26. Три предприятия
используют два вида сырья: уголь и
древесину. Заданы матрица расходов
сырья
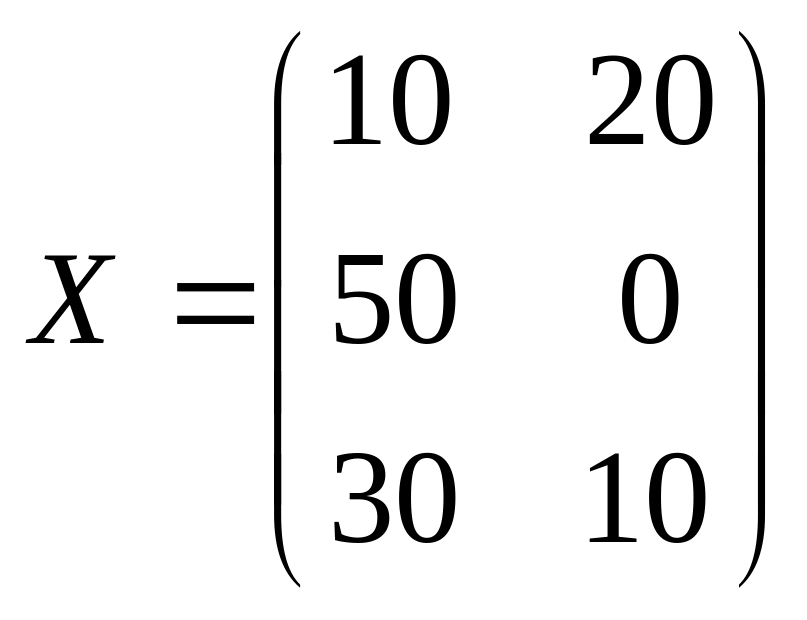 и матрица стоимостей перевозок тремя
видами транспорта
и матрица стоимостей перевозок тремя
видами транспорта
![]() .
Определить матрицу затрат по видам
транспорта. Провести анализ результатов.
.
Определить матрицу затрат по видам
транспорта. Провести анализ результатов.
27. Три предприятия
используют два вида сырья: уголь и
древесину. Заданы матрица расходов
сырья
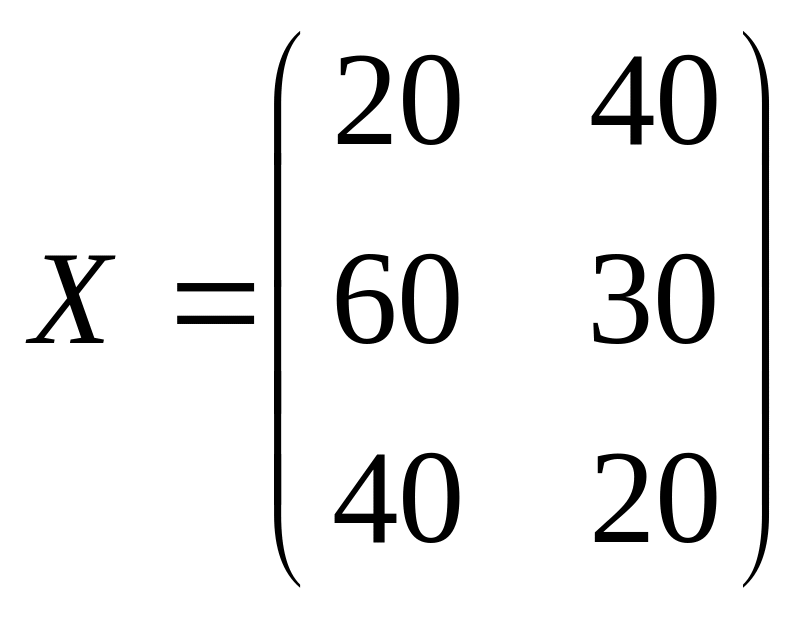 и матрица стоимостей перевозок тремя
видами транспорта
и матрица стоимостей перевозок тремя
видами транспорта
![]() .
Определить матрицу затрат по видам
транспорта. Провести анализ результатов.
.
Определить матрицу затрат по видам
транспорта. Провести анализ результатов.
28. Два цеха
предприятия выпускают продукцию двух
видов: 1-ый цех – продукцию 1-го вида,
2-ой цех – продукцию 2-го вида. Часть
выпускаемой продукции идет на внутреннее
потребление, остальная часть является
конечным продуктом. Требуется выявить
распределение между цехами продукции,
идущей на внутреннее потребление, и
общие (валовые) объемы выпускаемой
продукции
![]() ,
если заданы матрица прямых затрат
,
если заданы матрица прямых затрат
и вектор конечного (валового) продукта Y.
![]()
![]()
29. Два предприятия производят музыкальные центры, телевизоры, плееры. Количества продукции каждого вида, производимые за месяц, приведены в таблице 4.
Таблица 4
Вид продукции |
Телевизоры |
Музыкальные центры |
Плееры |
|
Количество продукции в условных единицах |
I пред- приятие |
100 |
300 |
200 |
II предприятие |
200 |
100 |
300 |
|
Данные о прибыли от реализации единицы каждого вида изделий в каждый из трех месяцев приведены в таблице 2.
Таблица 5
Месяц |
I |
II |
III |
Виды изделий |
Прибыль (в условных единицах) |
||
Телевизоры |
1,2 |
1,21 |
1,23 |
Музыкальные центры |
1,1 |
1,12 |
1,15 |
Плееры |
1,4 |
1,41 |
1,42 |
30. Два предприятия производят музыкальные центры, телевизоры, плееры. Количества продукции каждого вида, производимые за месяц, приведены в таблице 6.
Таблица 6
Вид продукции |
Телевизоры |
Музыкальные центры |
Плееры |
|
Количество продукции в условных единицах |
I пред-приятие |
200 |
400 |
100 |
II предприятие |
300 |
300 |
200 |
|
Данные о прибыли от реализации единицы каждого вида изделий в каждый из трех месяцев приведены в таблице 7.
Таблица 7
Месяц |
I |
II |
III |
Виды изделий |
Прибыль (в условных единицах) |
||
Телевизор |
1,4 |
1,1 |
1,2 |
Музыкальный центр |
1,3 |
1,2 |
1,3 |
Плеер |
1,2 |
1,3 |
1,4 |
